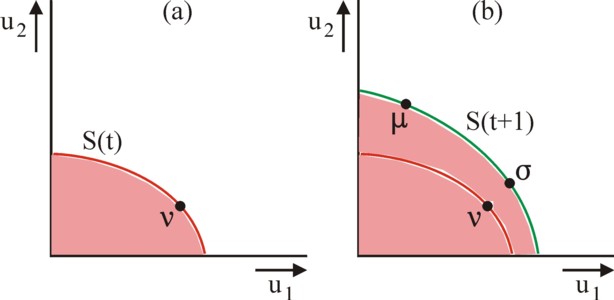
Figure 1: Utility possibilities for (a) state S(t)
and (b) state S(t+1) (μ before and σ after compensation)
Since about a year the Gazette studies models of the public administration. They can bridge the gap between theories from economics and the political science. Recently policy analysis has developed the actor-centred institutionalism, which indeed combines the best of these two worlds. Rational behaviour is restricted by the institutions. Besides, the form of action is taken into account. It turns out that policies can be described well by methods from the social choice theory. Notably game theory and the Hicks-Kaldor compensation principle provide insights in policies.
The Gazet has devoted various columns to administrative methods. The inductive method in the science of administration (organisational theory) has the problem, that it wants to analyze all factors of influence. However, their number is simply too large. Then it is rarely possible to increase the insights. The deductive method in the science of administration (rational choice paradigm) uses hypotheses of universal rules. This is an abstraction, but at least it allows for an empirical verification. Actor-centred institutionalism is not a deductive theory, but it does offer universally applicable theoretical frames. Then the policy analyst has at least something to go on. This is an improvement in comparison with the narrative approach of the science of public administration. However, before the hallmarks of actor-centred institutionalism are described, first the compensation principle of Hicks and Kaldor must be explained.
In a previous column it has been remarked, that the popular Pareto criterion does not suffice in making policy decisions. An economic state is Pareto optimal or efficient, when no other alternative leads to a higher individual utility for some, without reducing the individual utility of others. This criterion has the advantage, that inter-personal utility comparisons are not used. In other words, the utility evaluations of two individuals are not compared mutually. But unfortunately the Pareto principle is not very suited for testing the fairness (justice) of decisions. The Gazette has devoted various texts to the failure of the Pareto criterion in policy evaluations. The present paragraph repeats the argument, and continues with a profound analysis. During the writing the book Microeconomic policy analysis (in short PA) has often been consulted1.
First, already five years ago a column pointed out, that the utility improvement of an individual leads to a new frame of reference for his environment. The individuals, who use this frame of reference, will be less satisfied as a result of the change. One can accept this discontent, as long as the utility improvement of the favoured individual is the result of a reward for an excellent performance. But yet a hallmark of human nature is to long for some degree of equality (symmetry, anonimity) (p.161-162 in PA). Second, the Pareto principle accepts the existing state (the status quo). So notably no attention is paid to already existing injustices (p.161 in PA). The third objection against the Pareto criterion is actually the translation of the second objection for practical situations. Namely, the criterion can not be applied in practice. For, politics does imply the weighing of interpersonal interests (p.160)2.
Therefore it is not surprising, that for years and years science (as well as the Gazette) tries to find better criteria. Since more than two centuries (so even before the Pareto criterion) utilitarianism has been used in welfare studies. Utilitarianism measures welfare as a collective utility function, the social welfare function (in short SWF). The SWF aggregates (accumulates, sums) the utility of all individuals. According to utilitarianism it is a general interest to maximize the SWF. It is true that the method uses the Pareto criterion, but subsequently it tries to find the most just Pareto efficient point. An alternative approach, Nash bargaining, can also be interpreted as a form of utilitarianism. Justice is always related to the collective utility distribution. Sometimes utility is equated to money (a transferable utility).
Note that utilitarianism links up with practical measures for political decisions. For instance, politics attaches value to growth of the national income or the gross domestic product (GDP)3. The present paragraph wants to describe the Hicks-Kaldor compensation principle, which also tries to increase the available welfare. Consider a society, which consists of K individuals. Together they produce N goods, with total quantities qn (n=1, ..., N). At the time t the society is in a state S(t). S(t) defines the legislation, the available production techniques, the assortment of goods, the quantities qn of these goods, and therefore also their prices pn. Besides, in S(t) the available goods can be distributed in certain manners among the individuals. This distribution naturally partly determines the social productivity.
Note that in each conceivable state S(t) a maximal production can be realized. It is evidently also possible to produce less, as a result of waste. The maximal production is a hyper-plane in the N-dimensional space of q. In case of two dimensions this is called the curve of production possibilities. However, the Hicks-Kaldor compensation principle considers the utility possibilities, and not the production possibilities. For, the production possibilities do not directly supply information about the social distribution. Let uk(qk) be the utility, which individual k derives from his package qk of goods. So now one tries to find the hyperplane in the K-dimensional utility space of individuals, which corresponds to the maximal (efficient) production. As an illustration the figure 1a shows the curve of utility possibilities (red) for K=2. The curve corresponds to S(t).

Each point on the curve S(t) corresponds to a certain distribution of q among the K individuals. In the figure 1a the point ν is drawn as an example of a fixed distribution. Unfortunately the compensation principle does not address the fairness of ν. Namely, the Hicks-Kaldor principle states the following: a policy change from ν (on S(t)) to μ (on a curve S(t+1)) is an improvement, when it is possible to redistribute the produced goods q in μ in such a manner, that in the resulting point σ (on S(t+1)) one has uk(t+1) ≥ uk(t), where at least one individual has uk(t+1) > uk(t) (p.164 in PA). In other words, the compensation principle compares different states, and therefore different curves. This is called a potential Pareto improvement (p.164). In the figure 1b a curve S(t+1) is shown (in green), as well as again the curve S(t).
The figure 1b shows, that S(t+1) is an improvement in comparison with S(t), in the sense of the compensation principle. It is true that the individual k=1 is worse off in μ, but the situation S(t+1) allows to compensate k=1 for his loss, and yet maintain the improvement of k=2 (point σ)4. One indeed has σ1 > ν1 and σ2 > ν2. The figure 1b shows, that in the point σ the individual k=2 has transferred utility to k=1. However, the reader may realize, that in fact the individual k=2 transfers goods or money, which have utility value for k=1. These are true material compensations (side payments). This reality is shown in an adapted version of the compensation principle: a policy change from ν to μ is an improvement, when compensations are possible to make each individual indifferent (neutral) with regard to the transition. Moreover, the sum of all these compensations must be positive.
In this formulation the indifference still refers to the individual utility uk, but the compensations are material (p.167 in PA). The application of this adapted version is called a cost-benefit analysis (p.166)5. It is more convenient than the original compensation principle, so that in the remainder of the column the new version will always be used. The cost-benefit analysis requires the calculation of all compensations. Therefore use is made of the compensated demand curve, which has been discussed in a previous column. The compensated demand curve q = φ(p, u) describes the demand in such a manner, that the individual always remains indifferent. In other words, he keeps his utility u at a fixed value, for instance ν. The indifference is realized by compensating possible changes (in prices p) by means of the income y. This compensation Δy is called the compensating variation CV.
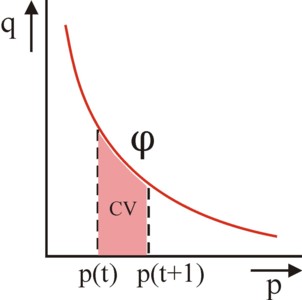
Concretely, the definition of CV is: in a state with utility μ (at a time t+1) the compensating variation CV is the size of the income change, which the individual brings back from his new utility μ to his original utility ν (at a time t) (p.144 in PA)6. The figure 2 illustrates the manner to calculate CV on a partial market with a single price change, from p(t) to p(t+1). The starting point is the compensated demand curve q = φ(p, ν), in red. Now, by definition CV is the integral of φ between p(t+1) and p(t) (p.146, 158-159). In other words, CV = ∫p(t+1)p(t) φ dp. Its value is the pink surface in the figure 2, with an added minus sign. Since the price rises, the income must also rise, with |CV|. After this elaboration on the CV the Hicks-Kaldor compensating principle can now be formulated as a mathematical inequality (p.167):
(1) Σk=1K CVk > 0
In short, the sum of compensation payments and takings must be positive. This is only possible, when the policy change from S(t) to S(t+1) is accompanied by productive growth. On the one hand this outcome is trivial. But in this form it yet leads to fascinating insights. For instance, define the lost utility during a rising price as Δuk = uk(p(t), y) − uk(p(t+1), y). In the figure 1b this is νk − μk. For a sufficiently small CV, it is simple to calculate Δuk, namely
(2) CVk = Δuk / λk(t+1)
In this formula λk(t+1) is the utility value of a unit of money for the individual k in the state t+1 7. A combination of the formulas 1 and 2 leads to (p.171 in PA)
(3) ΔW = Σk=1K CVk = Σk=1K Δuk / λk(t+1)
The formula 3 defines the variable ΔW. This can be interpreted as a change of the social welfare function W. The compensation principle in the version of the formula 1 guarantees, that the value of the SWF increases. The marginal utilities λk(t+1) are the weighing-factors in the SWF. Note that the marginal utility of money diminishes, according as the individual k has a higher income. Apparently the compensation principle (for a small CV) has the surprising consequence, that the interests of the richer individuals have a larger weight (p.171-172)! Therefore the SWF of the compensation principle has a concave form. This weighing conflicts with for instance the model of the economist K. Binmore, which relates the weighing factors to egalitarianism. In other words, thanks to the compensation principle a productive growth is guaranteed, but apparenlty not yet a just distribution.
Now this is not an insurmountable objection. For, a fair redistribution can be realized, after a growth path has been selected by means of the compensation principle (p.170, 173 in PA). First the compensation principle is applied in order to guarantee, that the policy yields growth. In the second step the effect is studied, that is imposed by the efficiency of production on the social equality. Here a distinction must be made between various social groups. In the third step politics attaches a weighing factor to the interests of all these groups. The policy choice follows from the aggregation of all weighed interests, so that growth and the distribution are just.
The book Games real actors play (in short AP) by F.W. Scharpf is the first publication, which systematically presents the theory of actor-centred institutionalism9. Actors are individuals or groups. In this latter case the actor is called corporate10. Actor centred institutionalism (in short AGI) assumes, that actors behave like a homo economicus. His behaviour is (boundedly) rational, and defends the (enlightened) self-interest. So this model assumes, that policy is realized in a power struggle between actors (p.43 in AP). They derive their power from the means, which they possess (p.11 in AP). There is no central actor, which plans and executes policies (p.11).
However, the actors are not entirely free in their actions. Society has institutions, which dictate norms, procedures and roles (p.16, 22, 39, 72, 180). They guarantee a certain predictability of actions (p.21, 40). Institutions are often based on morals. Indeed policy makers choose their problem definition, agenda and solutions in a normative way (p.13). This is an obstacle for the science of public administration, which tries to realize positive studies (with the exception of specialities such as post-modernism and the critical theory, which therefore are pseudo-scientific). But thanks to the modelling of institutions this aspect can yet be taken into account, without making the rigorous assumption of the homo sociologicus (p.21, 180). The institutions can be described by models with the help of game theory, which analytically is purely positive (p.5, 12).
ACI distinguishes between four categories of institutions: the anarchy, the network, the association, and the hierarchy (p.47). Here loyal readers immediately recognize the taxonomy of group archetypes by the economist P. Frijters. The networks of Frijters have as their only hallmark, that members have mutual contacts. In ACI the networks already have some cohesion and durability, perhaps more than Frijters assumes (p.136). Examples are coalitions or movements11. Associations are groups on the basis voluntariness, such as clubs. Associations and hierarchical organizations are so cohesive, that they possess morals. Thus the institutions limit the interaction of the actor in two ways: via the communicative structure and via actor-morals.
ACI distinguishes between four categories of interactions: unilateralism (one-sided action), the negotiation, the vote and the command (p.17, 46 and further). Since anarchy does not have norms, it allows only for mutual observations and influence12. Only the unilateral action is possible. The actors expect, that the others will react (boundedly) rational (p.20). Actors in a network will commonly negotiate. Here rights are often already available, such as private property and the binding contract. Unilateralism naturally remains an option. The association has a collective goal and property, so that decisions by means of votes becomes possible (besides the lower forms of interaction) (p.57). Finally, in the hierarchy all forms of interaction are possible. Unique for this institution is obviously the order.
Often the hierarchy is the most appropriate institution. Then the decisions are imposed on the actors as a dictate, so that sufficient support for the policy must be available (p.153 and further). This limits the transaction costs. In pluralism it is essential to avoid the occurrence of voting cycles (p.156 and further). A convenient management of the political agenda furthers stability, but also undermines the fairness of the decisions (p.159-160). For, the compensation principle itself does not offer guarantees. Therefore the communication perspective in the public administration advocates reflection, debate and deliberations (p.161)13. Scharpf mentions the limitations of the communication perspective: in practice all involved actors remain rent seeking. There is a conflict about the distribution, which affects the democratic deliberations (p.164). Scharpf even believes, that parliament does not primarily defend the general interest, but tries to curb the executive power (p.166)!

Besides the institution and the interaction, ACI uses a third concept of policy, namely the constellation (say, structure) of the actors (p.44-46). The constellation defines the elements of the game, namely the involved actors k (k=1, ..., K), and the available utility outcomes uk and strategies sk (p.89)14. The utilities take into account the morals of each actor k. For, solidarity, altruism, etcetera lead to dependencies of the various utilities uk (p.85-86). One may think, that the constellation determines the game, and therefore also the interaction. However, ACI believes that in the public administration the interaction must be studied separately (p.44, 72). The decision in a game can be made via each of the four interactions. Then the morals are determined by the interaction orientation (p.84). ACI makes morals explicit by dividing game theory in the constellation and the interaction15. The figure 3 shows schematically the policy cycle in the ACI form (p.44).
It is clear, that the various elements of ACI influence each other. Institutions affect the interaction orientation (say, the moral attitude), which again affects the constellation. But the interaction as a form of communication (unilateralism, etcetera) is only chosen, when the constellation has already been established. The policy model in the figure 3 has at least the advantage, that the used actor-model is rather realistic and credible. The actor is capable of feeling sympathy for others. He makes his choices by optimizing his utility. So he does not unconditionally obey the christian Golden Rule or the Kantian categorical imperative (p.21)16.
Nevertheless, the scheme in the figure 3 naturally is an abstraction. There is a salient difficulty to attribute (neo-)corporatism to an institutional category. In corporatism the state establishes administrative structures, so that the deliberations are no longer a network (p.141). Scharpf prefers to use the word regime for corporatism. So the categories of institutions must actually be refined further than the four mentioned categories (p.46). In the regime the structures have the effect of discouraging unilateralism (p.142). Regimes are relatively durable (p.142)17. It is surprising that the hierarchy of the state leads to a better functioning of regimes and networks (p.200 and further). For, the supervision of the state stimulates the private actors to conclude their negotiations with agreements! This point will be analyzed further in the sub-paragraph about the compensation principle.
Thus the judgement of ACI must be positive. The deductive theory never takes into account all effects, and sometimes neglects the context (p.33). In public administrations general laws do not hold (p.37). The real influence of subjective actors is ignored (p.37). Sometimes the theory even denies, that a stable state can exist (p.31, 102). But inductive descriptions of the state are scientifically not more satisfying (p.38). ACI at least offers an analytical frame, although these are not universal laws (p.30, 37). One may hope, that the analytical frame expands, according as ACI develops (p.30). Empirical data remain indispensable for those aspects, where the theoretical analysis of ACI exhibits lacunae (p.37).
Scharpf makes a fascinating attempt to integrate welfare economics and game theory in ACI. This provides policy analysts with mathematical instruments for studying policies. Welfare economics, notably the compensation principle, gives insight in the efficiency of the policy options, and the conflict of distribution. And thanks to game theory, even in a simple form, the possible strategies of the actors can be listed, as well as the political stability of the various options. Moreover, welfare economics gives a deeper insight in the institutions and interactions, whereas game theory is very appropriate for modelling constellations. The following sub-paragraphs elaborate on these methods.
The compensation principle of Hicks and Kaldor has just been explained, mainly because it is an important instrument in ACI. The compensation is represented by the formula 2, and then has the form of indifference lines Σk=1K CVk = ΔW, where ΔW is a positive constant (p.91-92 in AP). The figure 4a shows such a field of indifference lines (in red and green), for K=2. The policy O represents the status quo, where new policies are relinquished. The compensation criterion prohibits all policies with ΔW <0, such as the policy A. But it accepts the policy B and even C. It is true that in C the actor k=1 has a negative CV1, but thanks to the positive ΔW the actor k=2 is capable of compensating this. According to the compensation principle this policy is socially desirable.
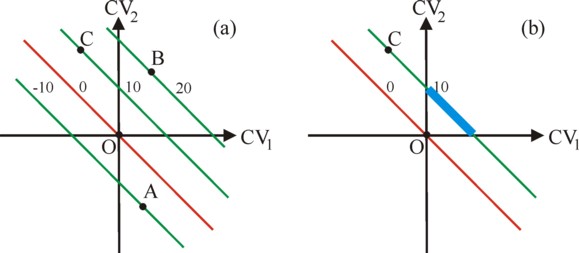
Now it becomes clear, why ACI pays attention to institutions. For, at the policy C a central actor must hierarchically enforce compensation. In the anarchy or network this is not possible. At most a minimal order can be achieved, which prevents causing damage (such as in the states A and C). Actors behave in such a manner, that CVk ≥ 0. This is called negative coordination (p.112-114). Only the states in the positive quadrant are allowed. The state C can not be reached, although it is a social improvement with regard to O. The reason is, that negative coordination already imposes boundaries on the distribution, because in essence unilateralism is egocentric. The Hicks-Kaldor compensation principle wants to delay the policy of distribution to a later phase. But Scharpf again gives a central role to the distribution with the graphical version of the compensation principle in the figure 4.
This can be illustrated clearly by studying bargaining, say within a network or association (p.119-120). Usually O describes the state, which results without an agreement (called BATNA). The negotiation tests the alternatives for policies with the help of the compensation principle, just like the central actor in the hierarchy. The central actor only tests for the sake of his cost-benefit analysis. He is not necessarily obliged to also execute the compensation. Perhaps he wants to use the policy for correcting the income distribution18. However, the negotiation is an interaction, which takes into account the distribution. The actors negotiate on the basis of their own interest, and not about collective growth. Actors, who are in danger of losing as a consequence of the proposed alternative (say, k=1 in state C), will only agree, when their loss is compensated.
The negotiation actually determines the distribution of ΔW among all concerned actors. Then the final policy will still remain restricted to the positive quadrant. This is illustrated in the figure 4b. Here the actor k=2 would like to reach state C. Since the actor k=1 can block this (otherwise bargaining would be unnecessary), he must be compensated. This compensation minimally equals the CV1 of the state C. In the state after compensation CV1=0 would hold. However, when the actor k=1 is rational, he will try to appropriate as much as possible of the growth ΔW! For, the actor 2 will reject state C only at CV2=0. Therefore the whole blue linepiece in the figure 4b is accessible as the final state after compensation (p.126-127)19. Bargaining leads to an efficient result, provided that the transaction costs remain low (p.116 and further).
Note that the political exchange (logrolling, package deal) is an alternative for compensation, when a payment in money is not acceptable (p.128). For completeness it is worth mentioning, that the consequence of the interactions is, that the state O will deviate from the status quo. Both the negotiation, the vote and the command can question the status quo (p.122-124, 172, 199). In the negotiation this is self-evident20. In the vote or the command the central actor can enforce the policy. His hierarchical power allows him to change the future status quo. Namely, he threatens the adversaries with a sanction, when they block the policy (p.172 and further). A particular case occurs, when the state engages in a hierarchical supervision of bargaining in networks or in corporatism (p.197 and further). In the hierarchy the option of the command can always be used as a threat!
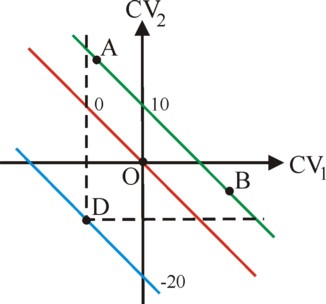
Namely, consider the figure 5, where two private actors bargain about a policy state (p.199). The states A and B are both socially desirable, but each hurts one actor. Furthermore, suppose that the state can change the status quo by means of subsidies, legislation and regulation in such a manner, that both actors are hurt by it (p.200 and further). The state can use this as a threat to enforce an agreement. Then the BATNA of the private actors shifts from the status quo O to, for instance, the state D. An observer in this point will conclude that both the policies A and B are beneficial for the two private actors! Now an agreement is likely. The two private actors engage in self-regulation (p.202). There is a synergy between bargaining and the hierarchy, which emerges, because both bargaining and the command are a possible interaction of the hierarchy (p.205)21.
Scharpf prefers to model the constellations of actors by means of game theory22. Game theory is capable of modelling and presenting decisions in a clear way (p.45). The interested reader can here and there in the Gazette find explanations of game theory. This will not be repeated in the present column. Games identify the available strategies sk (targets) of the actors, as well as their results uk (p.99). This allows to find stable outcomes (p.7, 100). In game theory this is called a Nash equilibrium. The identification of equilibria is important in policy analysis, because decisions can be unstable, notably when using votes based on a majority. See also p.155 and further in AP. Often the actors can reach an equilibrium by using a mixed strategy. However, Scharpf believes that in practice such a strategy is not feasible (p.102)23.
| orientation | individualism | solidarity | ||
|---|---|---|---|---|
| A2 cooperates | A2 exploits | A2 cooperates | A2 exploits | |
| A1 cooperates | 1, 1 | -1, 2 | 2, 2 | 1, 1 |
| A1 exploits | 2, -1 | 0, 0 | 1, 1 | 0, 0 |
Several striking applications of game theory in Games real actors play deserve attention. By far the most well-known game, also in policy analysis, is the prisoner's game (prisoner's dilemma) (p.75). This game is presented here again, in table 1. It is very useful for illustrating the benefits of collective morals. Suppose that the utility function of actor k is given by uk = vk + β×vj (p.84 and further in AP)24. In this formula vk and vj are the narrow personal interests of the actors k and j. Thanks to the second term in uk the actor k yet includes the utility of actor j in his decisions. This is called the interaction orientation of k (p.84). To the left in the table 1 both actors act as individuals (β=0). The equilibrium is (0, 0) in the lower-right square. Completely to the right in table 1 they engage in solidarity (β>0, here β=1). Now the equilibrium is (2, 2) in the upper-left square, and this is an improvement in comparison with (0, 0), so that here apparently an orientation of solidarity pays off25.
In policy analysis the relevance of the interaction orientation is controversial. Some policy analysts believe, that in the public sector the moral orientation must be leading in activities. They adhere to the communication (cultural, normative, constructivistic) perspective. However, Scharpf believes, that professional (individual and corporative) actors behave rationally, and will curb their emotions (p.87). He does admit, that even in a pluralistic society the collective norms can be purposively constructed (p.161 and further). But such actions commonly yet have the hidden aim to further a narrow group interest (rent seeking). It has just been remarked, that it is impossible to avoid the distributive conflicts (p.164).
| dependency | two-sided | one-sided | ||
|---|---|---|---|---|
| A2 prefers p1 | A2 prefers p2 | A2 prefers p1 | A2 prefers p2 | |
| A1 prefers p2 | 1, 1 | 2, 3 | 1, 2 | 2, 3 |
| A1 prefers p1 | 3, 2 | 1, 1 | 3, 2 | 1, 2 |
Furthermore, game theory can model dependencies. This is illustrated in table 2 (p.140-141 in AP). Suppose there are two actors k (k=1, 2), who each want to execute their own policy programme pk. However, they depend on the support of the other. The left side of table 2 presents the outcomes for mutual dependency26. There are two Nash equilibria, namely the lower left and upper right, so that it remains uncertain which programme will eventually be selected. However, suppose that the actor k=2 receives extra means, so that he can also reach an acceptable outcome on his own. He improve his BATNA or reservation utility, as it were27. See the right-hand side in table 2. This makes actor k=1 independent of k=1, because the choice for his own programme p2 yields the best outcome, irrespective of the strategy of actor 1. There is a unique equilibrium in the upper right.
But game theory also has its limitations. For instance, sometimes the game of a corporate actor is modelled. But this is in practice still a collective of groups and individuals. Therefore, strictly speaking also the actions within the organization of the corporate actor must be modelled with a game. This is called a nested game (p.32, 83 in AP). Furthermore, there are many games with a large number of actors. Then it is preferable to restrict the analysis to a small group of truly decisive (powerful) actors (p.79). Or various actors are combined into a single corporative actor, such as a coalition (p.80). The examples in Games real actors play are almost all dyades (with K=2).
Actor-centred institutionalism fits well with the method, which the Gazette tries to develop for policy analyses. Therefore your columnist read Games real actors play with pleasure. However, there is no reason for euphoria. Scharpf writes in his introduction (p.2): "Empiricists have not responded with great enthusiasm". And (p.6): "The reluctance of empirically oriented political scientists to use game-theoretic concepts seems to have two reasons. First, (...) much of the literature (...) is in fact practically inaccessible to the uninitiated. Moreover, empiricists (...) are generally repelled by the extreme unrealism of the assumptions". However, actor-centred institutionalism is still young, and your columnist trusts that all will end well.