Figure 1: Sets of utility possibilities:
(a) shift by disutility O;
(b) shift by rising status ν1
This column elaborates on the model, which Binmore uses to describe social morals. The source of empathy is traced back to primitive tribes. It is explained how Binmore attaches value to individuals. It turns out that the individual utility options have an effect on the chosen utility distribution. The theory of morals of Coleman is also explained, and compared in a calculation with the model of Binmore. Finally the various specific aspects of the models are separately addressed, such as the status quo and consensus.
Since its foundation, the Gazette has searched for a model of the homo sapiens. The starting point was always the homo economicus. Soon nuances were added, by comparing it with the Leninist image of man, namely the homo politicus. Incidentally, this image of man can perhaps better be called the homo sociologicus. It is characterized by the obedience to collective morals. At the end of 2014 in a column the interesting image of man has been described, which is proposed by the Dutch economist P. Frijters. In his view the individuals submit to their group, because this has personal advantages. This submission has the consequence, that the preferences of the individual change. The model of Frijters is supported by the social psychology, including group theory.
More than a year later the rational choice theory of the sociologist J.S. Coleman is described, which interprets collective morals as a social capital. Norms make the behaviour better predictable, and therefore reduce the transaction costs. In networks power and authority are transferred, just like products are exchanged on the market. Although also Coleman believes that the internalization of collective morals is conceivable, he yet attaches less meaning to it than Frijters. Recently the mentioned columns have been complemented with the view of the mathematician K.G. Binmore, who returns to the image of man of Adam Smith. Then collective actions are explained by means of the human capacity to feel empathy for other individuals. Since empathy furthers cohesion, it can create social morals, although these will be different for each culture1.
Binmore depicts empathy as the social deliberations behind a veil of ignorance, where nobody knows his present social position. Everybody acknowledges the uncertainties of life, and therefore abstracts from his own reality for a moment. The idea of constitutional deliberations in order to determine together in consensus the social morals originates from the philosopher J. Rawls. However, Binmore connects this idea with the bargaining model of Nash. The convention engages in collective bargaining, and finally chooses he most attractive type of society. The morals have the form of a democratic evaluation of the various group interests in society. On the one hand, the decision guarantees an optimal welfare (utilitarianism), and on the other hand the decision guarantees a stable growth, where nobody is left behind (proportionality, or the maximin principle).
It is obvious that none of the mentioned models represents reality. Each image of man highlights a certain aspect of reality. Often the choice for a certain model is determined by the specific circumstances, which the groups must face. Nevertheless, the model of Binmore excels in its wealth of knowledge, which supports the various assumptions. A limited number of plausible arguments is sufficient for explaining the social morals and its evolution. Thus Binmore presents a solid frame of thinking to political economists. The frame of thinking obviously remains controversial, and is indeed attacked by many opponents. But until now your columnist has not seen a convincing refutation2. Therefore the present column will again elaborate on the model of Binmore, and discuss some of its most interesting building blocks.
The cornerstone of social morals is empathy. Binmore states, that the evolution of mankind has progressed relatively favourably, precisely thanks to empathy. He assumes, that the groups with the most effective morals will win in their struggle to survive3. This struggle exists already since the emergence of life on earth. In the wandering groups of hunters and foragers in prehistory the individual group members already noticed, that they do not succeed in finding food on each day. Conversely, others in the group sometimes gathered more than they themselves could consume. Thanks to their emphatic capacity they concluded, that the risk of starvation can be reduced by putting all food in a collective fund. Each day everybody can obtain a fair share from the fund. The participants must naturally in advance conclude a contract about the distribution. This takes into account the individual skills.
Binmore describes a model, where the veil of ignorance merely leads to uncertainty about the individual catch on a certain day. See p.212-215 in the book Just playing (in short JP)4. Consider for the sake of convenience a situation with two hunters or foragers (n=1 and 2). Suppose that x is a portion of the fund. The utility of x is respectively u1(x) and u2(x). Take for the sake of convenience u1(x) = u2(x), and call this u(x). Suppose that daily only a single hunter has such a large catch, that he can contribute to the collective fund. Experience shows, that each day the probability is p1, that hunter n=1 has a big catch. Then the probability, that n=2 can contribute, is p2 = 1 − p1. Now the hunters negotiate behind the veil of uncertainty about their contract. They do not yet know, who tomorrow will have a big catch and will contribute to the fund. But the contract dictates, that tomorrow the lucky hunter will obtain a fraction χ from the fund, so that the unlucky hunter gets 1 − χ krijgt. Call them respectively r and a.
Therefore n=1 and 2 must rely entirely on the contract, which dictates as collective morals the distribution ur = u(χ), and ua = u(1−χ). The realities of the future remain concealed for them. The fund acts as an insurance against bad luck. Thus the expected utility is
(1a) E(u1) = p1×ur + p2×ua = p1 × u(χ) + (1−p1) × u(1−χ)
(1b) E(u2) = p2×ur + p1×ua = (1−p1) × u(χ) + p1 × u(1−χ)
Without contract the status quo is realized, which in a sense is also a contract, with χ=1. Behind the veil of uncertainty the status quo equals
(2a) E'(u1) = p1 × u(1) + (1−p1) × u(0)
(2b) E'(u2) = (1−p1) × u(1) + p1 × u(0)
Thus the contract with the optimal distribution χo is found by solving the Nash problem
(3) maximize for all χ in [0,1]: fN = Πn=12 (E(un) − E'(un))
Binmore uses the independency of linear utility transformations, and defines u(0)=0 and u(1)=1 (p.214 in JP). This simplifies the set 2a-b, and therefore also the formula 3. One finds (p.215 in JP)
(4) fN = p1 × (1−p1) × (u(χ)−1 − u(1−χ))² + (u(χ)−1) × u(1−χ)
Nevertheless the set of the formulas 3 and 4 can in principle only be solved, when the form of u(x) is known. A special case concerns two hunters, who are both neutral with respect to risks. Then here u(x) = x holds. The formula 4 gets the simple form fN = (4×p1 × (1−p1) − 1) × (1 − χ)² = -4 × (p1 − ½)² × (1−χ)² (p.215). So fN is maximal (just slightly negative) in the punt χ=1. Apparently risk-neutral hunters do not feel inclined to share. They remain at the status quo. Incidentally, this is logical, because the insurance fund does not add anything to the total catch. In short, the contract only makes sense, as long as one has ∂u/∂x > 0 and ∂²u/∂x² <0. Then u is a concave function, and the hunters are risk averse.
Another special case also deserves mentioning, namely when the hunters have identical skills. Then society is symmetrical in n=1 and 2, so that p1=½ holds. Then one finds fN = ¼ × (u(χ)−1 + u(1−χ))² (p.215). In the maximum of fN, u(χ)−1 + u(1−χ) must assume an extreme value. This case occurs, when the derivative equals zero. In other words, one has ∂u(χ)/∂χ = ∂u(1−χ)/∂χ. However, it has just been stated, that a fund will only emerge, when fN is concave. Therefore the mentioned identity can only be satisfied in the point χ=½. The optimal contract dictates an equal distribution of the fund. Incidentally, this is logical for a symmetric situation.
The deliberations about the contract in the described society of hunters is naturally less radical than the constitutional convention in the model of Binmore. The hunters can take into account in the contract their real position, as well as their own skills pn and their preferences un. Therefore the hunters need to show empathy only with their future Self, in the situation where they will be confronted with the real size of their catch (p.218). This is purely egoistical behaviour. Yet the example is clarifying, because it illustrates the evaluations, which a social convention will make. Each hunter does make an intrapersonal comparison, between his Self with and without contract. This also requires empathy. On p.302-303 in JP, Binmore indeed analyzes the situation, where the two hunters have their convention behind the veil of ignorance. This will be elaborated further on in this column.
The convention makes a decision about the social morals, by means of the recipe of bargaining according to Nash. A previous column has shown, that this recipe implicitly assumes an interpersonal comparison. The Nash solution combines utilitarianism and the proportional method (egalitarianism)5. Then the recipe is: choose the vector α of individual weighing factors in such a way, that the utilitarian solution σU and the proportional solution σP coincide. The concerned definitions are σU = {utility vector u in the set U of possibilities, which maximizes α · (u − ν)}, and σP = {utility vector u in the set U of possibilities, which maximizes γ = αn × (un − νn) for all n in (1, ..., N)}. In these definitions the utility vector ν represents the status quo. The model of Binmore assumes, that the interpersonal comparison is indeed possible, thanks to empathy.
It is interesting, that Bimore considers the socialist ideology as a form of utilitarianism. Namely, the central state uses the social welfare function W = α · (u − ν) as the morals, which dictate the distribution of the utility u (p.469 in JP). And the liberal ideology uses the proportional method, because everybody is treated equally. Now Binmore also gives an interpretation of the individual weighing factors αn (p.450 and further). In the short term, between two constitutional conventions, all αn are fixed. Both in utilitarianism and the proportional approach 1 util (unit of utility) of n has the same value as αn/αm utils of m (n≠m) (p.451). But the effects of these exchange ratios are different for the two ideologies (p.452). On the one hand, in utilitarianism αn/αm is the relative priority, that the utility of n gets in the optimization. On the other hand, in egalitarianism αn/αm is the number of utils of utility, which m must get, so that n gets an extra util.
Note that this weighing of utils is based on the social morals, and not on the individual valuation. An util naturally has the same utility for each individual. Here the utils of n and m s are empathically already fixed, and no longer independent of linear utility transformations. Next Binmore defines the social value wn of the individual n as 1/αn (p.399). This implies in egalitarianism, that wm utils must be given to m, when n obtains wn utils. The distribution is in agreement with the social value6. Here wn is not (exclusively) the market value of n, but the estimated value during the political process (p.455). In other words, wn is determined in a political struggle for power. Here Binmore indeed states, that the power is determined by the form of the Pareto boundary of the set U of utility possibilities (p.457). The value wn has been evolved in a historical process (p.458).
However, this representation of the situation implies, that in utilitarianism the individuals with a small value wn obtain a high priority in the distribution (p.452). This is a strange paradox. Socialists want to give to the poor, who are not very useful for society. According to Binmore, in daily life the individuals will find such a distribution unfair (p.453). They have an egalitarian inclination by nature (p.455). Binmore solves this paradox by stating, that needy individuals are desparate. They are prepared to make a large effort and take risks in order to improve their situation (p.460). It is precisely this property, which gives them power, and therefore they increase their value wn (p.463). For instance, at a certain moment in the class struggle the proletariat can perhaps gather more value than the bourgeoisie. At this moment a utilitarian will give a higher priority to the bourgeoisie (p.464)!7

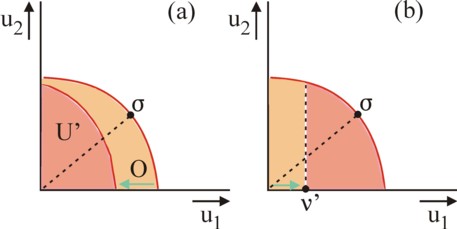
The effort to gain power is in fact rent seeking. It must not be confused with the effort to produce a lot. For, already Sam de Wolff, the namegiver of the Gazette, concludes that anybody, who works hard, experiences a disutility. The displeasure or disutility O reduces the utility of the worker (u'n = un − O), and therefore changes the boundary of the set U of utility possibilities. As an illustration the figure 1a shows the case with two individuals (N=2, ν=0), where the individual n=1 makes an extra effort at his job (p.465). The set U', which emerges after the correction for the disutility O, is smaller than U. Moreover the Nash solution σ is such, that now the individual n=2 will get a relatively large part of the available utility. Thanks to the changed shape of the boundary of utility possibilities (U' in the positive quadrant of the plane (u1, u2)) n=1 has apparently lost power. So by working hard the value w1 falls with respect to w2.
It can be concluded from this, that individuals with natural talents dispose of a higher value of wn (p.467). For, such an individual can produce with a reduced effort. Conversely, the acquisition of human capital requires an effort, which leads to a falling value of wn (p.466-467). Binmore also notes, that an increase of the individual status can be interpreted as an improved status quo. For, this increases the utility with, say, νn. According to Binmore the increase of an individual status does not lead to a different set U. The figure 1b shows this development for the individual n=1. The shift of ν actually implies a changed form of the boundary U in the quadrant with the new ν' as its origin. Again n=1 becomes less powerful, and his value of wn falls. Aristocrats are benevolent and austere (p.468).
Thus Binmore reconciles the apparent conflict between utilitarianism and egaliterianism with regard to wn. A high value of wn simply results from the acquisition of power, and from the possession of natural talents. Your columnist can not yet sum up all consequences of this model, but is impressed by its inventiveness. When the argument of Binmore is indeed sound, then it is a powerful instrument for abstract analyses of the individual value.
In the previous paragraph it has been concluded, that according to Binmore the form of the boundary of the set U affects the value of wn of the individual n. A large wn can be interpreted as much power. Your columnist has analyzed the case N=2, a society of two individuals, and tried to find the boundary, which gives relatively much power to the individual n=1 8. This is to say, the individual n=1 obtains the largest share in the distribution of the social benefits x. Therefore in this solution u1 will approach its maximum, whereas u2 remains far below its maximum. The distribution is determined with the help of the model of Nash. According to the property of independency of linear utility transformations, u1 and u2 may be scaled at will. Take as status quo ν=0, and as maximal value un=1 (n=1 and 2). See the figure 2.
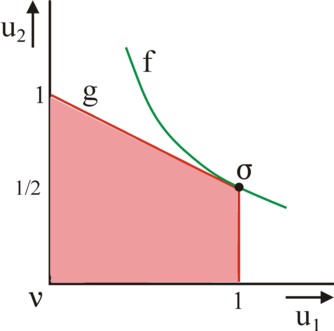
Consider the Nash curve u1×u2 = γ, where γ is a positive constant. It is the green curve in the figure 2. Define this curve as u2 = f(u1) = γ/u1. Define the wanted boundary of the set U of utility possibilities as u2 = g(u1). In a situation, where the individual n=1 receives his maximal utility, the Nash curve in u1=1 must touch the boundary of U. Then the Nash solution is σ = (1, f(1)) = (1, γ). Since u1=1 is by definition the right-hand boundary of U, the function g is perpendicularly downward in the point σ. See the red curve in the figure 2 9. A g is wanted, where σ2=γ remains far below 1, which indeed represents the "powerlessnes" of the individual n=2.
Since σ is a point of tangency, one must have f(1) = g(1) and ∂f/∂u1(1) = ∂g/∂u1(1). It follows that g(1)=γ. One also has g(1) = g(0) + ∫01 ∂g/∂u1 du1. Therefore one has γ = 1 + ∫01 ∂g/∂u1 du1. Note that the Nash curve satisfies ∂f/∂u1 = -f/u1, so that one has ∂f/∂u1(1) = -γ. This implies ∂g/∂u1(1) = -γ. Since U is a convex set, the function g of the boundary must be concave. Then it must satisfy ∂²g/∂u1² ≤ 0 on the interval (0,1). In other words, on the interval one has ∂g/∂u1 ≥ -γ. Insertion of the mentioned formula of the integral yields γ ≥ 1 − ∫01 γ du1 = 1 − γ. Therefore one finds γ≥½. Since here the boundary with the smallest γ is wanted, apparently one has γ=½. Then one has ∂g/∂u1 = -γ on the entire interval (0,1). Here the boundary g is a straight line. See the figure 2. And the individual 2 gets a utility σ2=½, which is 50% of his maximum10.
The found red boundary g in the figure 2 is actually logical. For, g determines the marginal rate of substitution MSV = du2/du1 at the boundary of U. The slope du2/du1 = -½ guarantees, that u1 can be increased on the boundary without hurting u2 too much. Only beyond (or in) σ1=1 the u2 fatally collapses on the boundary. As an illustration, consider again the figure 1a, where the powerless individual n=1 reshapes the boundary of the set U by his toil and moil in such a manner, that the new U' approaches the shape of the function g (with the axes exchanged, so that individual 2 toils, and not 1).
Previously in this column the situation of two hunters behind the veil of uncertaintly has been considered. The hunters can also deliberate behind the veil of ignorance. Here they lose all information about their own identity, with the exception of their individual empathy. See p.302-303 in JP. Binmore describes the negotiations in this constitutional convention with a complicated mathematical model, for the case N=2. Perhaps your columnist will once elaborate on this in the Gazette. The present paragraph merely wants to sketch the model, as it were a bird's-eye view. Represent the remainder of the hunters n=1 and 2 behind the veil of ignorance by I and II. First consider the individual I. His empathy-function is vI(un). This is to say, I values the state un (n=1 or 2) with the help of the function vI. There is a probability ½, that in reality he is the individual n=1. Otherwise he is n=2. Therefore the expected empathy with regard to reality is given by
(5) E(vI) = ½ × vI(u1) + ½ × vI(u2)
See for this formula p.291 in the book Playing fair (in short PF)11. The formula 5 expresses, that I must calculate his expected empathy-value for each point u in the set U of utility possibilities. The same argument can be used for the individual II behind the veil. His empathy-function is vII(un). So together the convention behind the veil is a set T of empathical utility possibilities, with elements (E(vI), E(vII)) (p.234 and further in JP)12. Now Binmore defines the constants α1(k) = vk(u1=1) and α2(k) = 1 − vk(u2=0), for k=I en II (p.293 in PF). From this it can be derived (p.294 in PF, p.233 in JP)
(6a) vk(u1) = α1(k) × u1
(6b) vk(u2) = 1 − α2(k) × (1 − u2)
The constants αn(k) are the weighing factors of the interests of the hunters 1 and 2, and together they represent the social morals. Then the problem remains, that the individuals k=I and II each have their own social morals. Binmore solves this on p.297 in PF and p.222-223 in JP by assuming, that k=I and II have the same empathy-function v(un). He justifies this assumption by remarking, that empathy results from the social evolution. Empathy is a collective phenomenon. Therefore the constant weighing factors αn(k) are identical for k=I and II 13. When now the formulas 6a-b are inserted in the formula 5, then the result is (p.294 in PF, p.436 in JP)
(7) E(v) = ½ × α1 × u1 + ½ × α2 × u2 + ½ × (1 − α2)
The formula 7 is the utilitarian welfare function, apart from the term ½ × (1 − α2) and the scaling with the factor ½. But these two deviations do not affect the point uP of maximal welfare. Now the two hunters behind the veil must choose the ratio α2/α1. This is done in the following manner. Suppose that I and II select the optimum uP, which maximizes the expected empathy-function E(v). In daily reality this optimum will favour one of the two hunters with respect to the other. A "philosopher-king" would be needed in order to maintain the contract (p.258-261 in JP). The individuals I and II reject such a benevolent dictator, because they prefer the democracy. Therefore the contract must be maintained by means of self-commitment (self-enforcing, self-policing contract). A previous column has shown, that this will succeed for a proportional distribution. Binmore derives, that here proportionality has the form (p.295 in PF, p.435 in JP)
(8) α1 × u1 = α2 × u2 + 1 − α2
The term 1 − α2 can be interpreted as the status quo (1/α1, 1). The formulas 7 and 8 together fix the optimal contract on the boundary of the set U of utility possibilities. This contract dictates the social morals in the equilibrium. Thus the ratio α2/α1 has also been fixed. A previous column has shown, that the contract is simply the solution σ of the Nash problem. This completes the justification of the model of Binmore. Your columnist is aware that this paragraph can only be understood, when the books of Binmore themselves are consulted. The paragraph is mainly meant to be a bookmarker in JP and PF14.
In the model of Binmore a social equilibrium is constructed, which is based on the value of individuals. Three years ago the Gazette discussed the rational choice theory of the sociologist J.S. Coleman, who does a similar thing. This model is presented in the fascinating book Foundations of social theory (in short ST)15. Coleman assumes a voluntary exchange of property by individuals. Such a situation is modelled with the help of the Edgeworth box. Thanks to the exchange the individuals can increase their utility with regard to the status quo ν, just like in the arbitrage model of Nash. The set U of utility possibilities resulting from the exchange is called the core. And the Pareto optimal boundary of U is called the contract curve. Coleman presents a method for determining the optimal equilibrium on the boundary of U, just like Binmore. Therefore in this paragraph both models will be compared16.
Apply for the sake of convenience the rational choice theory of Coleman also to the situation of the two hunters. According to Coleman the possession of resources yields power (p.133 in ST). For, the goods are desired by the other(s). Incidentally, the property can consist of the right to control events (p.33 in ST). The power, which the possession of a unit of a certain goods yields, is expressed by its value vk. Coleman defines the value as a system-variable (p.133). Therefore vk gets the same meaning as the price on free markets. Note that strictly speaking in an isolated community of two hunters the value vk remains indefinite. For, the hunters only take into account their personal preferences uk. The interested reader can consult the column about the consumer-surplus for an explanation of the difference between the price (value) and the individual utility.
In short, preferences and property are individual, whereas power and value are universal (p.133). Although Coleman does not explicitly mention this, apparently he assumes, that groups are embedded in the larger society. Then the value vk is imposed from outside on the group, because the individuals have an exit option. For instance, a hunter can exchange with individuals from a neighbouring tribe. Now the exchange options are determined by the budget constraint. In chapter 25 of ST the model is elaborated mathematically17. See the column about the perfect social system. As an illustration the model will now be applied to the society of two hunters. Suppose that the society has two goods k=1 and 2. This can be meat and vegetables, but perhaps also events, like hunting and resting. It could even concern rules, like freedom and equality - although it is difficult to exchange these between individuals.
The hunter n=1 has a utility function u1 = c110.6 × c120.4. In the same manner, the hunter n=2 has a utility function u1 = c210.8 × c220.2. Here cnk is the quantity of the good k owned by hunter k. The exponents depend on the individual preferences for the good k. For, they are equal to (∂un/∂cnk) / (un/cnk) 18. They express the intensity of the preference. Apparently the hunter 1 has a larger preference for the good 2 than the hunter 2. Furthermore it is important here, that hunter 1 and 2 both have an intense preference for the good 1. This implies that their preferences compete, so that the set U of utility possibilities is convex19. This is a requirement for the application of the model of Nash. Suppose that the status quo of the possessions is given by c11 = c12 = 4, and c21 = c22 = 6. So one has ν = (4, 6). The budget line of each hunter is rn = Σk=12 cnk×vk (more compact: r = C v). Since one has c1k < c2k, in the model of Coleman the hunter 2 is more powerful than 1.
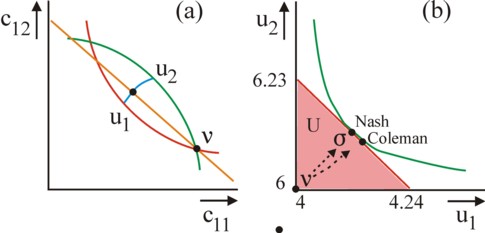
In this case the contract curve is given by 8×c11×c22 = 3×c12×c21 (p.678 in ST). It is shown schematically in the figure 3a, in blue. On the contract curve the utility of each hunter is at least as large as in the status quo. Thanks to the exchange the hunters can increase their utility. They must deliberate about the distribution of the benefits of the transaction (the increase in utility). Because of c11+c21 = c12+c22 = 10, it follows that the contract curve satisfies c12 = 16×c11 / (c11+6). Apparently one has on the contract curve u1 = u1(c11) and u2 = u2(c11), and therefore also u2 = u2(u1) 20. From this it can be derived that
(9) du2/du1 = -0.6295 × (c11 + 6)0.2
The marginal rate of substitution MSV clearly decreases with c11, so that the boundary of U is concave. Therefore U itself is indeed convex. The boundary is shown in the figure 3b. At the two ends of the contract curve one has u1 = 4.240 (at c11=3.432) and u2 = 6.235 (at c11=3.207). The MSV in these two points is respectively -0.9861 and -0.9813. Apparently the convexity is small, and the boundary of U is almost linear. Next the values of the goods k=1 and 2 can be calculated with the model of Coleman (p.684 in ST). They must be such, that the optima of the hunters on their collective budget line coincide. See the orange line in the figure 3a. The equilibrium of Coleman is the intersection of the contract curve and the budget line. Here one finds v1=0.07200 and v2=0.02801. This is to say, in the social equilibrium the exchange ratio is fixed as v1/v2 = 2.571. Then the total power r1 of hunter 1 equals 0.4, and similarly r2=0.6.
The material distribution in the equilibrium is c11=3.336, c12=5.717, c21=6.664, and c22=4.283 (p.683 in ST). Apparently hunter 2 has indeed more of good 1 in the optimum, due to his intense preference. Note that moreover the hunter 2 benefits from his larger power r2, because he can buy the cooperation of hunter 1 with the good k=2. The power would yield even more advantage, when the size N of the group and the assortment K of goods would increase. In the column about the model of Coleman the importance of the indirect exchange has been emphasized. Finally one calculates, that the optimal utility equilibrium is given by uC = (4.138, 6.100). See the figure 3b. Both hunters have improved their position with regard to the status quo, and hunter 1 the most, despite his lesser power. The hunter 2 must pay for his intense preference for the good k=1. Those who are choosy, suffer the most due to social scarcity (10 units of good 1).
Now consider the arbitrage model of Nash. This must be applied to the set U, which is given by the contract curve, with as status quo ν = (4,6). According to Nash the optimal distribution is given by his solution σ. In this point the boundary of U and the Nash curve (u1−4) × (u2−6) = γ touch each other. See the figure 3b. The Nash curve has the MSV du2/du1 = -(u2−6) / (u1−4). Insert in the right-hand side the formulas for u1(c11) and u2(c11), and equate this MSV of Nash to the formula 9. This yields a rather complex expression for c11, which must be solved by trial and error21. One finds as the optimum of Nash c11=3.332, c12=5.702, c21=6.678, and c22=4.298. These values differ significantly from those in the model of Coleman (see the previous calculation). The corresponding solution is σ (= uN) = (4.123, 6.115). See the figure 3b. Nash gives less benefits to the hunter 1 than Coleman does22.
In σ the MSV has the value -0.9840. This is also the slope of the corresponding utilitarian welfare function fU. In other words, one has α1/α2 = 0.9840. Assume α1=1. Note that with this choice the whole boundary of U in the present example coincides almost with fU = 10.34. For, now one has
(10) fU(u) = u1 + 1.016 × u2
Therefore the interest of the hunter 2 has a larger weight than the interest of the hunter 1. The path of the status quo ν=(4,6) to the optimum σ will follow the proportional line of self-commitment, namely u1−ν1 = 1.1016 × (u2−ν2). The hunter 1 with the largest value indeed gets more additional utils on the growth path than the hunter 2. According to the model of Binmore their social values are w1=1 and w2=0.9840. Since according to Binmore a large value is caused by a large power, in his model the hunter 1 has the largest power. The form of the boundary of the set U of utility possibilities is to his advantage. Compare this with Coleman, who interprets purchasing power as real power. However, a large purchasing power can not prevent, that somebody with intense preferences occasions large prices, so that yet his utility possibilities remain limited23.
The introduction of this column calls the interpretation, which Binmore gives to the arbitrage model of Nash, controversial. The market model of Coleman indeed gives another optimal distribution than the morals model of Binmore. Each model chooses its own equilibrium on the boundary of the set U of utility possibilities. In substance the two models start from different theoretical assumptions, which complicates a comparison. Binmore attaches values wn to the individuals, based on the social morals. Coleman attaches values to goods, so that in his perspective the individuals merely own a value rn due to their properties. He replaces the political choice of Binmore by an economic choice24. Nonetheless, both models have fundamentally many aspects in common. For instance, they are based on the individual utility functions, and so they use the methodological individualism.
The previous paragraph has shown, that Coleman has his own perspective on social morals, the constitution, and norms. He elaborates on this in his pioneering book Foundations of social theory. Binmore limits his analysis to the bilateral deliberations, because behind the veil group interests do not exist. However, Coleman sees society more as a network of groups (p.330). He prefers the positive social theory, which believes that the veil of ignorance is simply in contradiction with reality (p.345)25. The positive theory assumes, that individuals weigh their own benefits and costs during deliberations about norms. Then there is no longer any consensus, but merely a clashing of individual interests (p.345). The power (possession rn of means) determines how the constitution is formulated. Therefore the constitution is biased (p.348). It is true that there is empathy, but this is included in the individual utility function.
In large anonymous groups the norms and institutions must become formal (p.326). Relations of authority are formulated, which together form the constitution. According to Coleman they also include various informal institutions (p.327)26. The interpersonal comparison of utility is done by means of the relative power (p.352-353). The power is an indicator of the interests (benefits and costs), which individuals have. Groups with large interests will "buy" their rights (by means of exchange). Therefore Coleman is less worried than Binmore, that society will become unstable. For, the equilibrium is maintained due to the continuing exchange of resources, which are used to satisfy the needs of the individuals (p.37-40 in ST). However, the exchange is ony possible in a society with institutional guarantees. The individual behaviour is only restricted by collective norms, when there are rational reasons, such as the existence of externalities (p.325 in ST).
In many cases the groups will not all support the constitution (p.352). Some groups are too weak to veto the constitution (p.353-354). Then the optimality of the constitution is imposed, because the total sum of benefits and costs is still positive. Contrary to what Binmore assumes, the groups are sometimes not capable of renegotiating the constitution. Incidentally, in practice the imposed constitution will often make certain individual rights inviolable (p.356). Groups can accept an unfavourable constitution, because it is better than nothing (p.354). Some constitutions are not democratic, such as school regulations (p.349). So Coleman relies more on coercion than Binmore, who believes that only self-committing (self-policing) norms are viable. However, in cases with coercion the obedience to the constitution is not self-evident.
The group members must preferably have an exit option, because this forces the authorities to somewhat take into account the general interest (p.357). A decision by the majority will obviously be more legitimate than an authoritarian dictate (p.359). Social capital also helps, because it implies trust (p.359 and further). Furthermore, a division of power will further justice (p.363). Just like Binmore, Coleman acknowledges, that individuals are inclined to infringe the constitution, when this is to their advantage. Therefore institutions must be established, which maintain the various norms (p.327). The supervisor is an executive body, so that the principal-agent problem occurs. The maintenance itself causes costs, which can block the realization of a collective norm. See p.271 in ST and the corresponding column in the Gazet27. All in all, Coleman and Binmore clash on many points.
The American economists J.M. Buchanan and G. Tullock introduce already in 1962 (so ten years before Rawls) the idea of the veil of ignorance. Your columnist knows their work from the book Public choice III (in short PC)28. They make the interesting proposal to completely regulate the social redistribution of incomes in the constitution. Next parliament can focus on the evaluation of group interests. The constitution must make an inventory of the yields of all conceivable individual actions &phi, and subsequently determine which of these actions must be prohibited or enforced (p.616 and further in PC). For instance, suppose that there are two groups of hunters, n=1 and 2, with Nn members each. The action φn of the group n gives it a utility v(φn), and creates an external effect with utility or disutility e(φn) for the group m≠n. Therefore the social utility of the action φn is (p.620)
(11) W(φn) = Nn × v(φn) + Nm × e(φn)
Note that this W is a utilitarian welfare function29. The group utility is weighed with the numbers. In the constitutional convention the individuals do not know, to which group they belong. They will allow actions φn with W>0. However, when such an action leads to v(φn)<0, then the group n will not execute it. Therefore in this situation the group n is obliged to engage in this action by the constitution. Actions φn with W<0 will be omitted, as long as one has v(φn)<0. But when one has v(φn)>0, then the constitution prohibits this action. Prohibitions and obligations can be translated in voting rules (p.622 and further). For instance, a prohibition can be necessary in the situation Nn/Nm < -e(φn) / v(φn). Suppose that one has v(φn)>0, then all members of group n want to execute the action. The members of group m≠n oppose it. The constitution can block the action by dictating a vote, which only allows the action when the majority is 1 / (1−v/e) or more.
Thus parliament could decide with a qualified majority about all actions. The minority is always capable of vetoing actions, which would hurt the total social utility W. Therefore the representatives of the people can defend the interest of their rank-and-file in an egoistic (self-regarding) manner, without taking into account the general interest (p.616). Since this model ignores empathy, it belongs to the same type as the model of Coleman. Binmore would perhaps reply, that the group n will not accept the voting rule30.
When the constitution is interpreted as a social contract, then it must be approved on the basis of unanimity. Unanimity (consensus) is possible for allocative decisions (p.144 in PC). Decisions about the distribution always lead to a conflict of interests31. There is a zero-sum problem. In these cases unanimity is difficult, because the disadvantaged people will use their right to veto. A deadlock will result (p.143). Even when a compromise is possible, then yet the transaction costs can be high (p.138). Binmore eliminates the individual interests by hiding them behind the veil. And he evades the deadlock by assuming that the shared culture leads to a collective empathy. It is controversial whether this situation behind the veil resembles reality32.

According to Binmore the constitutional convention must deliberate about reforms of the status quo. The starting point is the existing distribution of properties, which has emerged during a historical development. However, the historical distribution is by no means just. Now the constitution must define the property right (p.139). It is unlikely, that the wealthy individuals are prepared to deliberate behind the veil of ignorance. But without this veil no consensus will be realized about the property rights. Then the requirement of unanimity perpetuates the injustice. Only a decision by the majority remains (p.140). But then the danger of the dictature by the majority, which exploits the minority, is present (p.142)33.
In the column about the homo economicus, published more than four years ago, it is remarked that the Dutch economist P. Frijters and others use an individual utility function of the form un = f(vn(xn), v1, ..., vn-1, vn+1, ..., vN). This is to say, the utility of the individual n depends on his wealth xn, but also on the utility vm of the other N−1 members of his group. Then the individual n is an altruist, because he can increase his own utility by making others happy. Binmore also believes, that an individual is willing to share his wealth with others. However, he believes that such an action is not a conscious choice, but an innate behaviour. It helps to improve the spread of the personal genes, and therefore primarily benefits family members. See p.413 and further in Just Playing. According to Coleman the individual is a pure egoist. For, in his model all interactions are an exchange. Pure altruism is unilateral34.
Therefore theoreticians, who sees man as an altruist, will object to the models of Binmore and Coleman. The economist H. Gintis states in his book The bounds of reason (in short BR), that human nature does support altruism35. This type of altruism is not charitable, but aims at reciprocity. There is a desire to cooperate. In this sense there is yet a relation of exchange. Therefore Gintis expects altruistic punishments, when an individual wants to discourage the egoistic behaviour of others. Individuals are not merely self-regarding, but also other-regarding (p.49 in BR). Gintis believes, that for instance in the well-known prisoner's dilemma game cooperation does occur. He supports his statement with the results of psychological experiments, which are done in laboratories (usually with students as test subjects). Such studies can be part of behavioural economics.
Gintis concludes, that pro-social and virtuous behaviour occur frequently (p.51 in BR). An accompanying phenomenon is the aversion of inequality (p.51). The ultimatum game shows, that punishing injustice yields satisfaction. Here one person obtains a sum of money, which he can share at will with another. A 50-50 split is the most common result (p.61). Unfortunately the reliability of such experiments is controversial. According to Binmore cooperation will only occur in durable relations (games with repetition). The test subjects in the laboratory mistakenly believe, that the test game will be repeated. Besides, according to Binmore the test subjects are rewarded insufficiently, so that they have little incentives for investing in a sound decision (p.30 in JP).
Gintis also calls to mind, that the efficiency wage stimulates workers to make an extra effort (p.62 and further). Reciprocity is a widely shared norm. Often misbehaviour is punished by bystanders, who do not directly benefit from this (p.66). Incidentally, Binmore also believes, that social control exists (p.310 and further in JP). In experiments it turns out that the test subjects punish, even when they themselves suffer from this, and can not hope for a later gain (p.70 in BR). Gintis is even convinced, that individuals appreciate virtue. He calls the morals a meta-preference (p.78 in BR). For instance, many individuals only lie, when the truth would lead to high costs (p.77 in BR). Nevertheless, Binmore and Coleman see sufficient indications for the existence of the calculating homo economicus, whereas Gintis does not.
Thus the total picture of human nature remains confusing. It is notably unclear, whether altruism is simply a well-understood personal interest. Coleman believes so. Binmore believes, that the innate self-sacrifice in families inadvertently has been extended to groups (p.421-422 in JP)36. Self-sacrifice is actually a means to spread the personal genes. Gintis and Frijters believe, that people are innately social, and inclined to cooperate. Incidentally, Gintis acknowledges, that altruism is often limited to the personal circle (p.79 and further in BR)37. So the difference between all these thinkers is gradual. But yet the consequences for the order of society can be radical. The personal experiences determine, which model the reader himself will prefer.