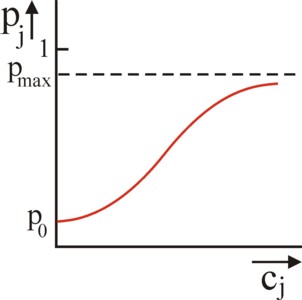
Figure 1: probability of success p1(c1, c2)
for a fixed c2
Economists become more and more interested in the social evolution, which is driven by the interactions between interest groups. The present column briefly discusses several essential aspects of evolution, such as group dynamics and the search for a good policy mix. The aim is to establish a social equilibrium. This is illustrated with an explanation of the coordination problems between groups, free riding within the group, and the application of game theory and population models on the evolution.
Within new institutional economics (in short NIE) it is popular to descrive the social development as an evolution of institutions. Institutions are maintained by collectives, and therefore are the subject of study for the social psychology and sociology. The institutions are formed at the micro- and meso-level of the society, in the small and large groups. A distinction is made between commercial groupen, which act on market, and non-profit groups, which are called the civil society1. The society is pluralistic. Many of these groups complement each other in a network, and reinforce each other.
However, it is unavoidabel that groups also clash, due to their different goals and institutions2. This has psychological reasons3. On the one hand, within the group there is a collective pressure on the individual to cooperate and adapt. Therefore the composition of the group becomes homogenous. There is mutual trust. On the other hand, the groups are mutually inclined to compete. A groups wants to distinguish itself from the other groups. The group commonly uses stereotypes and even biases with respect to outsiders. Groups defend their own interest (rent seeking behaviour). Sometimes groups try to eliminate each other. Consider religions, or political ideologies4. Therefore group actions lead to positive or negative external effects for their environment. The externalities are called a public good5.
The mediation between all these group interests is an important task of the national state. The voluntary submission of the groups to the state can be interpreted as the conclusion of a social contract. The competition between groups is moderated by the national constitution. The administration of the state itself naturally also consists of various groups. Apparently the institutions are maintained and changd by a mix of the civil society, the market and the state. The composition of the mix continuously changes in a dynamic process. For instance, during the decades immediately after the Second Worldwar the regulation by the state became popular, but since the eighties of the last century the appreciation for the free markets increases again. The NIE studies two aspects of collective decisions: (a) the rational evaluation, which often are based on the maximization of utility; (b) moral views, which emerge from the group identity.
A year ago the Gazette paid attention to the theory of interest groups, within the frame of rent seeking. Rent seeking commonly serves the personal interest. It is evidently conceivable, that the personal interest of a group coincides with the general interest. The lobby for a cause leads to costs, which must be covered by the members of the group. Therefore it is important, that the group motivates its members. In this manner the group obtains at least some durability6. The group morals or ideology must notably be strong, when the desired goals is more a general interest than a personal interest. The group can try to reduce its costs by building up a network with other groups. This increases the number of personal relations, so that the members are tied affectively to their group7. According as the morals and the affection dominate more (type b), a model of utility maximization (type a) gives less insight.
Furthermore, the interest group must choose a strategy or approach for its actions. The strategy is the way, in which the group employs its means for its goal. Often used methods are convincing, argumenting, demonstrating, litigating, and fighting8. In this order the group power is increasingly used for coercion. According as more power is used, apparently the social support for the goal or change is less. Rent seeking causes huge costs for society as a whole9.
Interest groups can direct their activities explicitly on the innovation of social institutions. In a strictly economic sense their activities are not productive. Since the interest group does make costs c, on balance the social welfare diminishes. On the other hand, thanks to the institutional innovation the society can become more efficient. This was for instance the (wrong) expectation of the early socialists. The action gives the pressure group an expected utility of E(u) = E(π) − c, where E(π) is the expected value of the goal-realization (E of expected). The group will only engage in action, when E(u) ≥ 0 holds. This is a purely rational consideration (type (a)), although evidently the value of E(π) does depend on the moral dedication (type (b)). A mutual fight between pressure groups can be called a tournament, with as the first price the right to impose the personal institutions on society.
The economist Olson fears, that various small pressure groups will become entangled in an endless fight, which drains welfare. The degenerated pluralism causes an uncontrolled growth of institutions. Only a strong state would be able to maintain the general interest (the public goods). On the other hand, the economist Becker expects, that the activities of pressure groups cancel each other by power and countervailing power. Moreover, neutral organizations, such as the media and science, have a moderating influence. The arguments of Olson and Becker both contain a nucleus of truth10. In this respect the reader is reminded of the debate about social capital. The sociologist Putnam advocates it, but others point to the accompanying isolation and exclusion. Corporatism can stimulate harmony as well, but also lead to political impasses.

The interest group can also degenerate internally. Some group members are inclined to reduce their own contribution to the costs of the group action (free riding). This increases their own utility, because they do benefit from E(π) 11. Free riding occurs often, when the member believes, that his individual contribution to the costs of the action adds little to the realization of π. The NIE pays attention to such parasitic behaviour, because it slows down the institutional evolution. The Gazette has discussed various special cases of this phenomenon. On the other hand, there are good reasons to yet contribute12. Consider two fighting groups (j=1, 2), which both promote their own goal πj. In principle π1 and π2 are different. Each group j has a fund cj for paying its lobby. Let pj be the probability, that the group j realizes its own goal. Assume that the lobby is effective. Then one must have ∂pj/∂cj > 0 (see figure 1). Logical is also ∂p1/∂c2 < 0 and ∂p2/∂c1 < 0.
Now consider an individual k. His utility function is uk(π). Therefore the optimal π* of k can deviate from the goals of the group. Each interest group j likes to motivate the individual k to join it. For, k can contribute to the group fund cj of available means. The group j becomes more attractive for k, according as j approaches its goal πj to π* of k. Unless j is orthodox in its doctrine, it will adapt πj in such a manner, that many members are attracted. Thus j can generate sufficient cj, at least in comparison with the means, which are at the disposal of competing groups. In formula this is πj = πj(c1, c2), with j = 1 or 2. This model has a surprising consequence. Namely, now the individual k realizes, that he can influence the goal of the groups by becoming a member. This is especially true, when he will donate a lot. His utility becomes uk(πj(c1, c2)). The individual k can somewhat control his own utility yield by means of donations13.
In the columns about rent seeking, sometimes in combination with a tournament, only models are discusses where two interest groups or individuals compete. In these situations the best strategy for each groups is always clear. Sometimes fate decides, who will win the fight, but the expected outcome is already known. The political scientist P.C. Ordeshook describes in his book Game theory and political theory (in short GP) a fight between three interest groups, where a natural equilibrium is absent14. Each group j has its own project, which it wants to realize (for instance an institutional change). Each project causes social costs c during execution, which are equally shared by all three groups (so c/3 per group). When a project is realized, then the corresponding group has benefits of π, and the other two groups get nothing.
Thus a decision must be made about the three projects. Each group organizes a lobby in order to get approval for its own project, and in addition two lobbies in order to further a rejection of the other projects. Let the index of the personal project be ν=j. Then the group j makes available means or funds for its three lobbies with a size of kν(j), with ν = 1, 2 and 3. This is called the strategy gj of the group15. Together the three groups expend a sum κ(j) = Σj=13 kν(j) in order to influence the decisions about the project ν. Suppose that the probability of approval of the project ν is given by pν = kν(ν)/κν. That is to say, the probability of approval is determined by the means of the pro-lobby of the group j=ν, in proportion to the means of the against campaign. Now the expected utility of the group j=1 can be calculated as E(u) = E(π) − E(c), which here becomes:
(1) E(u1) = p1 × (π − c/3) − Σν=23 pν × c/3
Similar formulas hold for E(u2) and E(u3). Here it is clear, that the project of each group shifts 2×c/3 of the costs to society. Suppose that the groups j dispose of equal budgets β = Σν=13 kν(j). It can be shown, that in such a situation at least one equilibrium exists (see p.217 in GP). That is to say, there is at least one set of strategies or behaviours {g1, g2, g3}, which leads to a stable expected decision about the three projects. This equilibrium can be represented symbolically as {g1*, g2*, g3*}, and is a kind of silent social contract. Now after some calculations it is possible to determine the corresponding value of pν*, and subsequently also of E(uj)*. Namely, suppose that two groups have already determined their gj*. Then the remaining group can optimize his gj. Assume for the sake of convenience, that this is j=1. The optimum can be calculated by means of the Lagrangian:
(2) L = E(u1(k(1), k(2)*, k(3)*)) − λ1 × (Σν=13 kν(1) − β)
In the formula 2 the vector k(j) is a succinct notation of its components kν(j). This vector is simply an alternative notation for the strategy gj. The expected utility of j=1 depends on its own k(1), and on the optima k(2)* and k(3)*, where the budget imposes limits. The variable λ1 is the so-called multiplier of Lagrange. The optimum for j can be found by optimizing the Lagrangian, by means of a suited choice for kν(1). In other words, the optimum requires ∂L/∂kν(1) = 0 for ν = 1, 2, and 3. Substitute the formula 1 in the formula 2, then one has16
(3a) (π − c/3) × (κ1 − k1(1)) / κ1² = λ1
(3b) (k2(2) × c/3) / κ2² = λ1
(3c) (k3(3) × c/3) / κ3² = λ1
The groups 2 and 3 must obviously have used similar formulas in the determination of their optimal strategy. After some lengthy calculations (p.218-219) one finds with all these formuals, that in the optimum one must have κ1 = κ2 = κ3, k1(1) = k2(2) = k3(3), and therefore p1 = p2 = p3 17. This is to say, an identical sum is always spent for influencing a project. Moreover, each group spends the same sum on its pro-lobby. Therefore each project has the same probability of being approved. This probability can be calculated by combining the formulas 3a and 3b. The result is18
(4) p* = 1 − c / (3 × π)
Note that according to the formula 4 one must have c ≤ 3×π. A group will fight for her project, as soon as the outcome π is larger than her own costs c/3. She shifts the remaining costs 2×c/3 to society. However, as long as π < c holds, the project negatively affects the social welfare W(u1, u2, u3). The example is special in this sense, that the three groups impose identical burdens on each other. The formula 1 (and the equivalents for j = 2 and 3) show, that in the optimum of the group j one has E(uj)* = (π − c) × p*. In the situation π < c the group j opposes the projects, but it is not yet inclined to stop its own project. For, the damage is caused by the two other projects. Such a loss-making equilibrium is called Pareto inferior (p.220 in GP).

Furthermore, note that the calculated equilibrium is not unique. Namely, from the definition of p it follows that the equilibrium must satisfy (-1 + 1/p*) × k1(1) = k2(1) + k3(1). Combination of this equation with the budget-limitation implies, that k1(1) = β×p* holds. Apparently in the optimum the group 1 is yet free to make her own choice of the value of k2(1) or k3(1). The groups 2 and 3 have a similar freedom of choice. So there are indeed various equilibria {g1*, g2*, g3*}, which are, moreover, equal in E(uj). The situation of various equilibria is a problem for the groups j = 1, 2 en 3. For, each group makes its own choice of an equilibrium. Therefore the probability is significant, that the three groups will not select the same equilibrium. But then the outcome of {g1, g2, g3} will no longer be an equilibrium. The probability pν will differ for each project. This is to say, at least one group has an outcome, which is not her optimum19.
The harmed group will change her strategy gj, but without coordination, so that no equilibrium is formed. A chaotic time series of sub-optimal decisions results (p.220). Institutions are required in order to coordinate strategies, but the model does not include these. In the introduction of the present column it has been remarked, that the state can establish such institutions. The coordination is itself a public good20. Moreover, these institutions can enforce, that projects are rejected, when they reduce the social welfare W. This situation occurs for instance, when the project of the group j imposes negative external effects on the rest of society. There is a market failure. On the other hand, the rest of society could also be hurt, when the group j successfully seeks rent from the state. The state subsidizes the project of the group j. Then there is a state failure! (p.213)
Historically each state forms its own institutions, according to the specific circumstances. This creates a path dependency of the evolution. A Dutch example of coordination is the tripartite deliberation between the social partners and the state, for instance in the Social-economic Council (SER). The model with the three pressure groups shows, why this corporatism can fail21. As soon as the mutual deliberations stagnate, each group will independently choose a strategy. A decision trap can occur, so that corporatism becomes immobile.
The economist A. Drazen presents in his book Political economy in macroeconomics (in short PM) an interesting model of free riding (parasitize)22. Consider the simple case of a group with two members j = 1, 2. Each member must decide whether he will buy a certain public good. The good has a utility uk = π − ck for member k, where π is the outcome and ck the costs. So the strategy gk of member k in his decision to buy is "do" (d) or "leave" (l). It belongs to the set {d, l}. Since it is a public good, it becomes available for the whole group, without rivalry or exclusion. Therefore each group member benefits from avoiding the costs. See the table 1. It is obvious, that the member with the smallest ck will eventually buy the good. However, suppose that none of the members knows the costs ck of the others. They only know, that c is divided according to the cumulative distribution-function F(c) on the interval [0, cm]. This complicates matters.
| g2=d | g2=l | |
|---|---|---|
| g1=d | π − c1, π − c2 | π − c1, π |
| g1=l | π, π − c2 | 0, 0 |
First note, that such a situation is relevant for the evolution of institutions in time, such as public goods. For, each group member is inclined to wait until another pays for the good. Drazen calls this a war of attrition) (p.397, and more extensively p.432-439 in PM). An impasse results, so that the social development stagnates. However, for the sake of convenience a static situation is assumed. Then there will be a decision, and it must be an equilibrium g* = {g1(c1)*, g2(c2)*}. This represents the group contract. The equilibrium can be calculated. Namely, one can calculate that the member k will buy (gk=d), when ck ≤ π × (1 − p) holds. Here p is the probability, that the other member will buy23. The member prefers gk=l, when ck > π × (1 − p) holds. This is to say, when the member k is convinced, that the other will pay for the good, then he will omit this himself.
The model has a surprising consequence. Namely, the member k does not base his decision on ck ≤ π. He will omit the purchase already at costs, where paying actually is useful for him. This is due to his risk-neutral attitude. He accepts with resignation, that perhaps the good will not be available. Only the expected utility is relevant, not the worst conceivable utility. Apparently the inclination to free ride leads on average to a reduced supply of the public good. It puts a brake on the evolution of the good, and therefore on the innovation of the institutions24. Also in this case coordination can increase the collective welfare W(u1, u2). For instance, the group itself or the state can introduce regulation, where free riders are punished (p.389 in PM)25. Besides, the reader may remember from the introduction, that members can be motivated by means of moral and affective incentives (p.389).
The described model can be interpreted as a theory of the state (p.401 in PM). The column started with the hopeful model of Downs, where the members like to pay for their group, because in this manner they can influence the goals of the group. However, the parasitizing behaviour of individuals or even groups is a fundamental problem, which of old has stimulated philosophies about the role of the state. Since the seventeenth century these have taken the form of theories about the social contract. See also the book Individuals, institutions and markets (in short IM)26. Although since the indispensability of the state has not been controversial, the best administrative mix is still unknown. At the start of the column it has already been stated, that since the eighties of the last century the fear for state failure grows. Again and again the probability of state- and market-failure must be evaluated.
Such an evaluation is only possible, when the social evolution is understood. Thanks to the public choice theory and the NIE the knowledge about institutions has increased. Institutions often form in an organic manner, in a natural (spontaneuos) social process (p.80-81, p.90-96 in IM). They are invented at the meso level, by groups. Such institutions have been tested in practice for a long time, and naturally have some support (common law). But institutions can also be imposed at the central level by the state and its political leaders, at the macro level, for pragmatic reasons (p.91) (statutory law)27. The state has the monopoly on violence, and can stifle the resistance against its institutions (p.81, 149). Therefore in the evolution of institutions a choice must be made between two evils: (a) the chaotic competition between groups in the civil society, and (b) the dictature and the abuse of power by the armed political ruler.
It deserves repeating: the role of the civil society is two-edged. Interest groups can propagate both new institutions or block progress (p.95). Morals are a powerful means for mobilizing individuals as supporters of reforms. Unfortunately it is difficult to model these morals (p.97, p.106-117 in IM). As soon as an equilibrium forms between the various groups, actually a social convention has been established (also called routine or heuristics) (p.88, 101-105). The convention is internalized, so that the individual is guided by it. The rules of the game limit him in the choice of his strategies (p.106, 125). Although conventions are bound to a culture, it seems that the capacity to learn has a genetic origin28. Thus the individual learns the utility of reciprocity. The conventions form in a fairly simple manner at the meso level, within groups (p.127-129).
The state places the groups in the external frame of control at the macro level (p.129). The liberal state creates trust by means of the legal systeem (p.133, 143). The legislation protects the individual property, as a part of the civil rights. Property supports the unfolding of groups (p.147). The state can impress the laws, conventions and morals upon the individuals by means of the media, education, and similar formation (p.151). Thanks to this socialization of the individuals the supervision by the state can be limited. Moreover, the individuals have a voice as a result of the parlementary democracy. Politics will react to this feedback, as is apparent from the recent reformism in the social-democracy. Thus at least an integer state will take care, that the social game maintains a solid support (p.146, 156). On the other hand, it is costly for individuals to leave a perverse state by means of the exit option (p.137, 142).
The NIE assumes that the social institutions are selected in an evolutionary process. The groups with the best institutions have an advantage in their competition with other groups. Therefore they will grow at the cost of the groups with unsound institutions. The economist K. Binmore shows, that such a path of development can be modelled with game theory29. First consider the game of the prisoner's dilemma. This describes an interaction between two players 1 and 2, as well as the possible outcomes (u1, u2) of their interaction. The outcome uj (j=1 or 2) depends on the manner, in which the two players behave. Two actions are conceivable, namely cooperate (in short s) or parisitize (in short p). In other words, the behaviour gk of the player is an element of the set {s, p}.
| g2=s | g2=p | |
|---|---|---|
| g1=s | 1, 1 | -1, 2 |
| g1=p | 2, -1 | 0, 0 |
The table 2 summarizes the hallmarks of the prisoner's dilemma game. In the four squares the possible pairs of outcomes (u1, u2) are shown, for each combination {g1, g2} of actions. The table shows, that the social welfare function W(u1, u2) = u1 + u2 is largest, when the players both cooperate. Then W=2 holds. However, each player is tempted to parasitize on the other, since this yields more for himself (2>1). Therefore each player will prefer gk=p, which leads to W=0. The combination {p, p} is called the dominant strategy, because none of the players has an alternative, which certainly will yield more. It is tragic, but rational, to prefer gk=p. Therefore this will be the normal behaviour in a group of the type homo economicus.
| j=2 in A | j=2 in B | |
|---|---|---|
| j=1 in A | α, α | γ, δ |
| j=1 in B | δ, γ | β, β |
Next consider groups A and B of the type homo behavioralis. This is a completely different type than the homo economicus, because it is controlled by the institutions. It has fixed morals, a strategy, which can not be changed by rational reflections. Suppose that the group A always cooperates (gA=s), and the group B always wants to parasitize (gB=p). Suppose that both groups live together in the same society, and the A types form a fraction q, and therefore the B types a fraction 1 − q. Now a table can again be constructed, in this case of the outcomes in interactions of two members of society. See the table 3. This has a somewhat different meaning than table 2, because there is nothing to choose. In each interaction a member of A has an expected outcome E(uA) = q×α + (1 − q)×γ. A member of B expects E(uB) = q×δ + (1 − q)×β.
Now suppose that the outcomes lead to an evolutionary selection. The group with the highest expected outcomes will finally oust the other. Then for instance the group B will be ousted, when the condition q×α + (1−q) × γ > q×δ + (1−q) × β holds. Consider as an illustration a society of purely group A, where due to an accidental mutation sometimes a small group B forms. As long as the mutants B are ousted, the society of A remains evolutionary stable. Suppose that q almost equals 1, because actually the group B is only formed by mutation. When q can approach 1 arbitrarily close, then the condition for stability is α≥δ 30. For instance α=β=1 and γ=δ=0. On the other hand, when the values of the table 2 are inserted for α, β, γ and δ, then it turns out that the group A will be ousted by the mutants.
This application of game theory is interesting, because in this way the evolutionary soundness of various institutional actions (fixed strategies) can be studied. For instance, consider a society, where during the interaction both players can observe each others type31. Then each player can adapt his own behaviour to the type of the other. Suppose that the group C has an institution, which encourages actions of imitation (gC=i). In the interaction a player in C cooperates, when first the other has shown a willingness to cooperate. And the player in C wants to parasitize, when the other has also revealed this intention. Note that a society of purely group C will behave the same as A - although their institutions differ! Suppose again, that by an accidental mutation a small group B can form. Suppose that the outcomes are determined by table 2. This is to say, the outcomes of the prisoner's dilemma game hold.
In this society the interaction of a member of the mutants is always {p, p}, with outcome u=0. When a member of the group C interacts with a mutant, then his outcome is also u=0. When the member of C meets another member of C, them both must choose between the actions s or p. The rational choice for both is s, with u=1 as outcome. Thanks to the lucrative mutual interactions between the members of C, they have higher expected outcomes than the mutants. Therefore the mutants are ousted, and the society of group C is evolutionary stable.
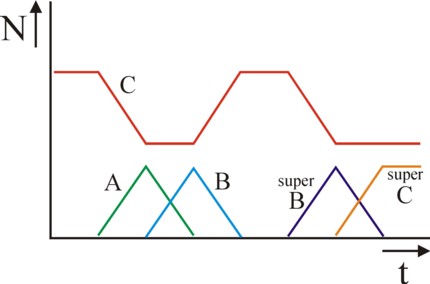
Unfortunately the group C is still not invulnerable. Namely, suppose that mutants A form. In the society of C the mutants A have the same outcomes as C. It is conceivable, that in the end the group A completely takes over this society. The able-bodied group C becomes extinct. When then subsequently small groups of mutants B emerge, then these will simply oust the group A. Apparently the development of institutions depends on the probability of mutations!32 It is logical that mutations have a preference (large probability) for simplification. This stimulates the mutation of C to A. On the other hand, as long as mutations B also form, then the group C keeps an advantage over its mutation A. Then the mutations B act like a kind of vaccination, which mobilize anti-bodies, so that there is still a probability of maintaining the institutional behaviour of C. See for this phenomenon the figure 3, on the left of the time line.
However, note that a mutation is conceivable, where the mutant B pretends to be a member of C. Then the act of imitation by the group C becomes unsound, because it actually degenerates into A. Now the "super" mutants B will oust the group C, and therefore reduce the welfare W. See the figure 3, on the right of the time line. Incidentally, there is yet hope, because a "super" mutant C can emerge, which does have the capacity to recognize the "super" mutants B! These "super" mutants C will oust the "super" mutants B. The original game between C and B has returned, albeit now with the extra option of disguise for B. See the figure 3, on the extreme right of the time line.
| g2=s | g2=p | |
|---|---|---|
| g1=s | 3, 3 | -2, 2 |
| g1=p | 2, -2 | 0, 0 |
It is useful to emphasize again, that besides the institutional behaviour (the fixed strategy) the outcomes (the social rewards) are also essential. For instance, consider again the homo economicus, but now in the stag hunt game33. This has other outcomes than the prisoner's dilemma game. One has α=3, β=0, γ=-2, and δ=2. See the table 4. In this game {s, s} is the dominant strategy, in the sense of Pareto. However, when the players have an interaction {p, p}, then the Pareto optimum can not be realized. For, who in this situation would choose gj=s, runs the risk to have an outcome uj=-2. The choice gj=p is evidently not rational. Yet it is conceivable, for instance when a player makes a mistake, or believes that gj=s is too tiring, or has a grudge34.
It depends on the mutual trust t, whether a player feels up to the behaviour. Suppose that t can vary between 0 and 1, so that it is a probability. The expected outcome of gj=s is E(u) = t×3 + (1−t) × (-2). The expected outcome of gj=p is E(u) = 2×t + 0. For a risk-neutral player j, gj=s pays, as long as t ≥ 2/3 holds. A fascinating aspect of the stag-hunt game is, that due to its specific rewards it has its own evolutionary selection. For, consider again groups of the type homo behavioralis. Contrary to the prisoner's dilemma game now the group A does remain stable with regard to mutants B (because α=3 > δ=2). The group A simply creates higher outcomes in the mutual interactions. And now in a society C also the small groups of "super" mutants B, which can disguise as C, do not stand a chance.
Game theory illustrates the moral evaluations, which the various individuals and groups make in their mutual interaction. Another approach is found in the population models, which describe the size of various groups35. The mutual interactions between the various groups have influence on the social distribution of power and welfare. Weak groups tend to shrink. Suppose that the society consists of groups A and B, with a size of respectively NA(t) and NB(t). Here t is the time variable. The dynamics of the composition of society can be described by the set of equations36:
(5a) dNA/dt = αA×NA − βA×NA² − γA×NA × NB
(5b) dNB/dt = αB×NB − βB×NB² − γB×NB × NA
The α, β and γ are model-constants. The idea of the set 5a-b is naturally to approach the really occurring phenomena by means of a simple mathematical expression. In this model the change of the population is determined by the three terms on the right-hand side of the formulas. The first term is simply the nett effect of births, deaths and migrations. There is a surplus for a positive α, so that in principle there is an exponential growth. The second term is the ousting within the personal group, which is caused by scarce available means. This term reduces growth for a positive β. The third term is the ousting due to the competing group, also because of scarce means, and perhaps also due to an outright hostile behaviour of that group. This term couples the two formulas, and describes the mutual dependency of the groups A and B.
Take for the sake of convenience αA = αB = 1, βA = βB = 1, and γA = γB = 2. This makes the formulas 5a and 5b identical, except for the exchange of NA and NB. This choice simplifies the argument, but it is otherwise neither necessary nor essential. Unfortunately even with this simplification the set 5a-b can not be solved exactly for NA(t) and NB(t). But it is possible and fairly easy to draw the paths of evolution in the (NA, NB) plane. This method is illustrated in the figures 4a-b. First consider the figure 4a. The horizontal NA-axis is NB=0. Due to the formula 1b one has dNB/dt = 0 on the axis, so that the axis is a path of evolution. Here NA satisfies the formula
(6) dNA/dt = NA − β × NA²
The formula 6 is called the logistic growth-equation. The formula 6 can be solved in an exact manner, and has the solution37
(7) NA(t) = 1 / [β − (β − 1/NA(0)) × e-t]
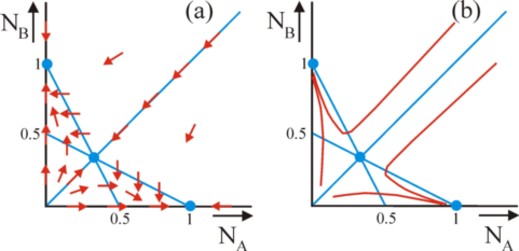
It has just been mentioned that in the present case β=1 is preferred. So for t→∞ one finds on the axis, that NA = 1. According to the formula 3, NA(t) evolves towards the value, irrespective of the start value NA(0). In the figure 4a this evolution is represented by arrows. This point, which can never be reached (unless NA(0) = 1), is an equilibrium. Because of the symmetry in the set 5a-b one finds exactly the same for the NB axis. Another interesting case occurs for NA = NB. For, insertion in the formula 1a again leads to the logistic growth formula 6, but now with β=3. The formula 7 is the solution. For t→∞ one has NA = NB = 1/3, and also this point is an equilibrium. Irrespective of the start value NA(0) = NB(0), the population evolves to this point. In the figure 4a this is also indicated with arrows on the line NA = NB. Note that om this line dNB/dNA = 1 holds. Such a line is called an isocline.
Next consider the equation NA − NA² − 2×NA × NB = 0. When this holds, then one has dNA/dt = 0. Two solutions are found, namely NA=0 and NB = ½ × (1 − NA). Apparently these lines are also isoclines. The last mentioned isocline is shown in the figure 4a, including the arrows for dNA/dt = 0. Because of the symmetry one finds a similar isocline for dNB/dt = 0. See the figure 4a. The intersection of the two isoclines is the just found equilibrium NA = NB = 1/3. The two falling isoclines divide the (NA, NB) plane in four parts, with in each part unique signs for dNA/dt and dNB/dt (namely (+,+), (+,−), (−,+) and (−,−)). In the figure 4a in each part the corresponding directions of evolution are indicated with a loose arrow (two for (+,+) and (−,−)). Thus in the (NA, NB) plane a flow- or direction-field is constructed, at least its most important hallmarks.
The figure 4b shows four typical paths of evolution in the (NA, NB) plane. It is clear that the two groups A and B are mutually quite hostile. For, all starting points at the left-hand side of the line NA = NB evolve towards the point (NA, NB) = [0, 1]. And all starting points at the right-hand side of the line NA = NB evolve towards the point (NA, NB) = [1, 0]. Again and again one group is finally completely ousted. Only a society on the line NA = NB develops in a stable manner, qua composition. However, also here a small disturbance will still lead to a complete ousting of a group. However, note that this dramatic situation is caused by the chosen constants in the set 5a-b. It turns out that for some other combinations of constants the paths evolve towards the central point of equilibrium, the intersection of the two isoclines38. Apparently then the two groups can be reconciled.
The preceding argument justifies the conclusion, that indeed the institutions of some groups can be ousted from society! Moreover the figure 4a-b shows, that in the immediate vicinity of the line NA = NB small differences determine, which of the two groups will finally win. Then there is not a clear superiority of the remaining regime in comparison with the ousted institutions. Apparently small changes in the policy of the state can have dramatic consequences, which do not in advance imply an improvement.
Obviously in each application it must be checked, whether the set 5a-b is a credible abstraction. For, this model has been developed for ecological systems, where the groups A and B are animal species with biological differences. When the model is applied to people, then this ignores the possibility, that the people can exchange their group39. In particular the interpretation of the third term γ×NA × NB in the set 5a-b is difficult, because the interaction between human groups can assume may forms. It is conceivable that the groups compromize, and harmonize their institutions. This would change the set 5a-b itself. Incidentally, this will rarely happen in the short term, because the hallmark of institutions is precisely their rigidity. According to the communitarism the identity of individuals is indeed mainly determined by their original group.
Furthermore note that the constants in the set 5a-b are not necessarily positive. For instance, when one wants to model the capitalist class struggle between the proletariat and the bourgeoisie, then there is not necessarily an evolutionary ousting. A predator-prey model is then more promising. Here the constant γ of the bourgeoisie is negative, so that she benefits from a growing proletariat. For, the proletariat is the labour force, which produces the surplus value. When the bourgeoisie grows too fast, then the proletariat will pauperize40. Despite the extortion the proletariat is no longer capable to appease the desire for surplus value of the bourgeoisie (as Marx would say). Therefore the predator-prey model leads to a periodical cycle of the size of the population, where the cycle of the predator (group B, such as the bourgeoisie) has a time lag with respect to the cycle of the prey (group A, such as the proletariat)41.