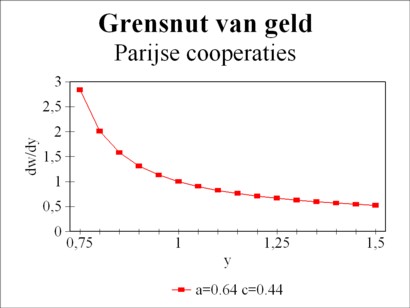
Figure 1: Marginal utility of money in Paris
Social welfare functions help to analyze questions regarding the distribution. They give insight in the moral choices of policy formation. The present column discusses several of these functions, and combines them with models of monetary utility, among others those of Ragnar Frisch. They are also compared with the justice theory of Rawls, albeit in the interpretation of Binmore. This knowledge is compared with older texts in the Gazette. Finally, related reports of the CPB and the WRR are discussed.
Six years ago the Gazette was mainly devoted to central planning, because it intuitively seems such a logical arrangement for the economy. Sam de Wollf, the name-giver of the Gazette, already invented a model, where the social partners optimize their utility in mutual coordination. Furthermore, at the time the Gazette analyzed the Leninist plan-theory, which commonly transforms policy into a target function Z. The optimal plan is the one, which maximizes Z. Such models have a time horizon T. Then the target function assumes the form
(1) Z(T) = Σt=1T p · x(t)
In the formula 1, t represents the period, so that Z(T) is actually a sum of partial target functions Z(t). There are N products, and during the period t a quantity xn(t) of product n is generated. Each product n obtains a value pn for the entire planning period T. The function Z(t) is simply the weighed sum of all product quantities. The Russian economist Val'tuck proposes a variant, where the weights pn are calculated from the x itself.
The formation of plans occurs also in the market economy, but they are commonly limited to the macro level. A familiar example of this type is the model of Solow, which uses the consumption c per household as the target function. The Dutch economist Tinbergen also has invented a macro model, which bases the policy on consumption. His method of analysis reminds of the approach by Val'tuck. In another model Tinbergen shows, that the national income Y becomes maximal at an optimal savings quote. Incidentally, Tinbergen also presents planning models for the micro level, for instance for the export policy. A disadvantage of these target functions is, that the policy goals are formulated by a (preferably) benevolent central dictator. One would actually prefer, that the policy goals are determined by the individual needs of the households or individuals.
Therefore the Gazette soon paid attention to the social utility function or social welfare function (in short SWF). Let the utility function of the individual k be uk, then the SWF equals W = W(u), where the vector u has the individual utility functions as its elements. This collective W replaces the central Z. It is true that even then a central policy remains inevitable, because the form of W must be defined. But at least W has been legitimized in a democratic manner, due to the input of uk. Next the Gazette studied the political philosophy, which must justify the transformation W(u) → Z(x(t), T). This shifts the interest of the Gazette to the individual autonomy and participation. Besides, in various columns the supposed advantages of central planning were rigorously rejected. W guides the policy, but it no longer is a complete plan.
Whereas the target functions Z(x(t), T) are designed for practical planning, the theory of the social welfare function is mainly based on collective morals. It wants to reconcile the individual freedom and social justice. The system must be reciprocal. Therefore this theory pays much attention to the question of the distribution of the national income. For instance, the SWF can be used in the design of the tax- or pension-system. Since the capacity of the production puts limits on the satisfaction of needs, an equilibrium must be found. Therefore the transformation W(u) → Z(x) actually works in two directions. Hence one must know the utility of money w(y) of individuals, before p·x is distributed. The present column will first analyze the utility of money, before the function W(u) itself is studied.
The Gazette has regularly paid attention to the subjective utility of money, because this concept contributes to the determination of justice in the income distribution. Already in 1931 the Dutchman Jacob van der Wijk developed a theory about the utility of money. Besides, he applied this theory to the Dutch income distribution. Following Bernoulli, he assumes that the utility of money ug varies with the height of the income y in a logarithmic manner. The theory describes the macro level, where the income of each individual is a given. Much later, in 1968, the Dutch economist Bernard van Praag used the assumption of Bernoulli for modeling the individual consumption at a given income y. Here the micro level is considered, so that the variation of ug,i as a function of y can be analyzed for each separate individual i.
Van Praag shows, that at the macro level the individual preference can yet be represented by a collective utility of money ug, although the individual peculiarities always cause some deviations from the collective trend. Building on these columns, in the present paragraph the theory of the utility of money by Ragnar Frisch will be discussed, as is described in his book Methods of marginal utility (in short MU)1. The theory of Frisch does not take into account the individual peculiarities, and therefore analyzes the preference at the macro level. Frisch takes as his starting point the utility function u(x, y) of an individual i. Here xn is the quantity of a product n (n=1, ..., N), and y is a money sum. Thus x is a vector of dimension N. Let pn be the price of the product n, and P the price level2. Now y is interpreted as the real value of the money sum, so that its nominal value equals P×y = η.
It is logical to define y as the amount of savings from the income (see p.13 in MU). In such a situation the second law of Gossen can be applied. This law states that in a situation of equilibrium the utility function must satisfy
(2) ∂u/∂y = (P/pm) × ∂u/∂xn
This is natuurlijk still a formula at the micro level. However, Frisch assumes that this utility function u is identical for all individuals. It represents the collective trend, or if desired, the utility of the representative person3.
Besides Frisch assumes, that this person spends his entire income on consumption4. Then it is preferable to define y as the income. One has y = p·x, where p and x are vectors of dimension N. Then it makes sense to write u(x, y) = w(y) + u(x). That is to say, for a given y the person simply optimizes the composition of x. However, when the income y changes, then also u(x, y) will change in a complex manner. Such effects are summarized in the term w(y), which will henceforth be called the utility of money. Next consider a single product m, with x=xm and p=pm, and assume that the quantities of the other products remain constant. Thus the formula 2 changes into
(3) ∂w(y)/∂y = (P/p) × ∂u(x)/∂x
This is called the equilibrium equation (p.16 in MU). Now suppose that thanks to empirical observations one disposes of the demand curve x(p, y) for the market of the product. Then these statistical data can be used, in combination with the formula 3, to determine the marginal utility of money ∂w/∂y. For, let x be constant. Then one has
(4) ∂w(y2)/∂y = (P2/P1) × (p1/p2) × ∂w(y1)/∂y

Select for instance ∂w(y1)/∂y = 1, then all other ∂w(y)/∂y can be calculated from this. When desired, w(y) can be found with the help of the integration w = ∫ (∂w/∂y) dy (Frisch does not do this). Frisch applies this method to the sales of sugar in various consumer-cooperative stores in Paris between 1920 and 1922. This file of data contains time series of x, p, P, and y 5. See the figure 1 for his results (p.32 in MU). It turns out that the behaviour can be described fairly accurately by the analytical relation ∂w/∂y = c / ln(y/a) (p.31). Note that this deviates from the Bernoulli model. For, that model leads to ∂w/∂y = 1/y. This conclusion is important, because the Bernoulli model is intuitively appealing: the utility grows in an absolute manner with a quantity dw, each time when the income increases in a relative manner with a factor gy = dy/y. See the of this paragraph for more comments.
Frisch also develops an interesting model for the supply on the labour market. Let v(t) be the displeasure, that is caused by working for t hours. A positive v implies a negative utility. In a previous column about the labour market it has been explained, that the total utility equals U(y, t) = w(y) − v(t). The optimization of the working hours requires an equal marginal utility and disutility: ∂w/∂t = ∂v/∂t. Application of the chain rule of differentiation yields
(5) (∂w/∂y) × ∂y/∂t = ∂v/∂t
Let z be the nominal hourly wage, then y×P = z×t holds. The working-hours t depend on the wage level z, that is to say, t = t(z). This function determines the supply on the labour market. The reverse (z = z(t)) is naturally not true, because the enterprise determines z. Ignore for the sake of convenience the influence of z on P (p.97 in MU). Differentiate both sides of the formula 5 with respect to z. Then one finds6
(6) ∂t/∂z = (∂w/∂y + y × ∂²w/∂y²) / (P × ∂²v/∂t² − (z²/P) × ∂²w/∂y²)
The formula 6 is fascinating. For, ∂w/∂y and y are positive. It is logical, that ∂²v/∂t² is positive and ∂²w/∂y² is negative. The denominator is positive, but the sign of the numerator is not known in advance. The formula 6 allows for the possibilitiy, that ∂t/∂z <0, so that the workers prefer longer working-hours t, when the hourly wage z falls! This phenomenon of the labour market has indeed been described already in a previous column about the pleasure of work. It is called the income effect, because the worker wants to stabilize his income. The neoclassical model of the labour market ignores this possibility. There merely the substition effect occurs. That is to say, a rising hourly wage makes the leisure time more expensive, so that the worker prefers longer working-hours t.
When the empirical formula ∂w/∂y = c / ln(y/a) of Frisch is inserted in the formula 6, with c>0 and y>a, then ∂t/∂z is positive for y > a×e 7. Frisch rejects the Bernoulli formula, such as ∂w/∂y = c/(y − m) according to Van der Wijk (c>0). For, then ∂t/∂z is always negative for a positive m, and positive for a negative m. Frisch believes that this is unrealistic (see p.31 and p.102-104 in MU). His criticism is not relevant for the analysis of Van Praag, because this holds at the micro level. There is no representative person. On the other hand, Van der Wijk is obliged to respond to the criticism. He does this among others in his book Inkomens- en vermogens-verdeling (in short IV)8. First, Van der Wijk tries to describe his own empirical data with both the Bernoulli formula and the empirical formula of Frisch. He concludes that the Bernoulli formula clearly fits the data best (p.97-99 in IV).
Van der Wijk also objects to the theoretical assumptions of Frisch. According to Van der Wijk, the utility of money depends on the application of the money, so that a universal utility of money does not exist. For instance, the wage (means of exchange) would have a different utility than money as invested capital (means for saving) (p.164). Van der Wijk even believes that the utility of money may be incommensurable with the utility of products. For, sometimes goods cause saturation, but this is never the case with money! (p.165). Moreover, Van der Wijk points to the statement of Frisch himself, that the price index P actually depends on y (P = P(y)) (p.164). The work of Frisch and Van der Wijk is so outdated, that since then science has probably invented a better model. Therefore your columnist does not take sides. Indeed, this paragraph is mainly intended to be a piece of economic history.
The economist F. Kalshoven has described the history of several Dutch economists, between 1883 and 1939, in his thesis Over marxistische economie in Nederland (in short ME)9. In paragraph 4.3 Van der Wijk is indeed mentioned. However, Kalshoven does not discuss his theory of income, probably because the thesis focuses on marxism. He does explain here, that Van der Wijk applies the philosophy of physics of L. Boltzmann on economics. According to Boltzmann the entropy of systems increases with time. This can be described by means of statistics. Now Van der Wijk wants to explain the macro level with the help of the micro level, just like Boltzmann, albeit for the economy (p.172 in ME). One could say, that Van der Wijk uses methodological individualism. This is a transformation of subjectivism into objectivism10.
Van der Wijk argues, that the members within a group gradually develop into a homogenous mass, due to their mutual interactions (p.171 in ME). Here he displays a sharp-witted insight in group dynamics, which enforces the individual socialization by means of group pressure11. But he also recognizes, just like institutional economics, that thanks to the evolution each group establishes its own concrete institutions. Thus for instance the political parties or national states obtain mutually conflicting points of view. Groups by nature create biases with regard to each other. Incidentally, Van der Wijk acknowledges, that empirical studies mainly yield objective data. Therefore, in practice the micro level must yet be derived from the macro level (p.173). Van der Wijk indeed uses this method in the formulation of his theory of income. The values of the utility of money in society simply have a normal distribution.
Two years ago the Gazette discovers the rational choice theory, and with it the methodological individualism and the public choice theory. Unfortunately it is extremely difficult to derive the social welfare function W by means of methodological individualism. This is a recent and abstract field of science. Therefore in these years the Gazette has not elaborated on this problem. However, the present column will again address the theme12. Here the focus is on practical applications. Those who appreciate a rigorous explanation of the underlying mathematical theory, can consult the voluminous book Microeconomic theory13. The general form of the SWF for a society with K members is14
(7) W(u) = Σk=1K gk(uk)
In the formula 7, gk(uk) is a yet to be defined function for the member k, which satisfies ∂gk/∂uk >0. This SWF is called universally utilitarian, because the contributions of all K members are simply added. Therefore the maximization of W can imply, that for instance u1 becomes quite large, whereas at the same time u2 becomes small or even negative. This unequal treatment is indeed a disadvantage of the form of the formula 7 15. Furthermore, nota that here one has a cardinal concept of utility. Besides, the utility can be compared interpersonally, due to the summation with respect to different persons16.
A logical choice is gk = αk×uk, where the constant satisfies αk>0. Then the formula 7 changes into
(8) W(u) = Σk=1K αk × uk
The SWF of this form is called purely utilitarian. Such a SWF has been proposed centuries ago by philosophers, for instance by Jeremy Bentham. Modern economists, such as J.C. Harsanyi, have derived the formula 8 with the help of a few simple assumptions17. Cardinality commonly implies, that the decisions based on utility are invariant under the transformation vk = ψk×uk + ζk, with constant ψk and ζk. The relative scale and the zero point can be chosen at will for each member k. However, due to the interpersonal comparison the invariance must be limited here to vk = ψ×uk + ζ (or the αk must be changed for a changing scale for k).
Another popular choice is gk = ln(uk − ζk), where uk > ζk holds. This form represents a situation, where the status quo of society at a time t=0 is given by u(0) = ζ. A policy is proposed, which for t>0 will improve the social situation. Now the function W is used for distributing the benefits for t>0 over the K members in a fair manner. The central ruler is no longer a planner, searching for a maximal yield, but plays the role of an arbiter for the distribution18. Since uk − ζk is a difference of utility, the zero point can now be chosen arbitrarily. Furthermore, the decisions are invariant when the relative utility scale is changed. For this choice of gk it is usual to do the calculations with eW instead of with W itself. That is to say, one assumes
(9) W(u) = Πk=1K (uk − ζk)
In the formula 9 Π is the mathematical symbol for multiplication, in the case of K separate terms. Loyal readers recognize in the formula 9 the model of an bargaining problem between K individuals, which has been invented by the mathematician J.F. Nash. The Gazette has used it already in the description of CAO bargaining, applications, contract modifications, pressure by interest groups, and state subsidies to an enterprise.
Frequently used is also the SWF of the form
(10) W(u) = minimum of (α1×u1, ..., αK×uK)
The decision of the central agent is determined completely by the utility uk of the least wealthy member k, with the constant αk as a weighing factor. Since the policy aims to maximize this utility, the formula 10 is called the maximin principle. It has been made famous by the philosopher J. Rawls. The theory of Rawls will be addressed again further on in this column19.
| distribution | utility member 1 | utility member 2 | utilitarianism | bargaining | maximin |
|---|---|---|---|---|---|
| a | ½ | 2 | I | I | II |
| b | 1 | 1 | II | I | I |
| c | ½ | 1 | III | II | II |
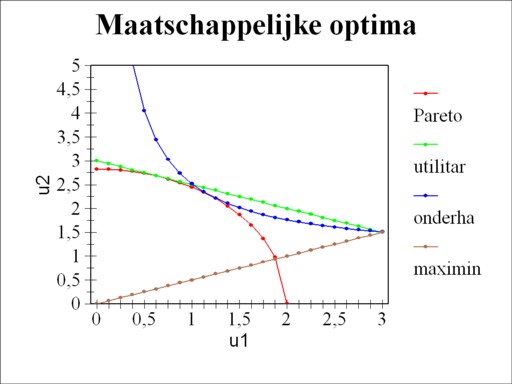
The policy rules of the formulas 8, 9 and 10 each have their own logic. Now it will be illustrated briefly what their consequences are. Consider in the table 1 a society with two members (K=2), and three possible utility distributions (a, b and c)20. The table gives for these three distributions the order of decreasing preference (I, II and perhaps III), which follow from utilitarianism, the negotiation, and the maximin principle. For the sake of convenience, αk=1 and ζk=0 is chosen. It is clear, that utilitarianism tries to find the largest total utility, and accepts inequality. The method of bargaining is prepared to give up some utility for the sake of equality. And according to the maximin principle the total utility is unimportant (indifference), as long as the least wealthy person benefits.
The meaning of the three SWF can also be clarified in a graphical manner, albeit only in two dimensions21. Consider again the society with K=2. Suppose that the possible combinations (u1, u2) are given by the formula 2×u1² + u2² ≤ 8. The Pareto optimal solutions are on the outer boundary of this area, namely 2×u1² + u2² = 8. In the figure 2 the Pareto curve is shown in red. First consider the utilitarian SWF, given by W = u1 + 2×u2. In the (u1, u2) plane the combinations with a constant W are represented by lines with a slope of -½. These are indifference-lines. The maximization of W requires, that a line is chosen, which is just tangent to the Pareto curve. In the figure 1 this is the green line. The optimum is [0.67, 2.67]. Since W gives an extra weight to member 2, he clearly has the highest utility in the optimum.
Next consider the SWF of bargaining, given by W = u1 × (u2-1). In the (u1, u2) plane combinations with a constant W are represented by hyperbolas with asymptots u1=0 and u2=1. Also here the hyperbola must be selected, which is just tangent to the Pareto curve. In the figure 3 it is drawn in blue. The optimum is [1.20, 2.27]. Apparently the distribution is more egalitarian than in utilitarianism. Finally, consider the SWF of the maximin principle, in the form W = minimum of (u1, 2×u2). The optimum must also now be located on the Pareto curve. This optimum must satisfy u1 = 2×u2. For, if this would not hold, then the minimum could still be improved by moving in the right direction across the Pareto curve. In the figure 1 the line u1 = 2×u2 is drawn in brown. The intersection with the Pareto curve is [1.73, 0.87]. The distribution is not completely equal, due to the unfavourable weighing factor of member 2.
In 2017 the Centraal Planbureau (CPB) published the report Distributionally Weighted Cost-Benefit Analysis. This report fits well with the discussion in the present column, and shows how the theory can be applied. The authors use for the marginal utility of money (or income) the formula
(11) ∂w(y)/∂y = 1 / yμ
In the formula 11, μ is an empirical constant with μ>0. As long as μ<1 holds, the marginal utility is here evidently larger than the one of the Bernoulli model (∂w/∂y = 1/y). The formula 11 is suited for imitating the model of Frisch (∂w/∂y = 1 / ln(y)), at least within a limited interval of y-values. This is clear from the fact, that for y>5 the function 1 / ln(y) is larger than 1/y0.5 and less than 1/y0.25. So a suited choice of μ between 0.25 and 0.5 will roughly approximate 1 / ln(y). However, note that Frisch actually rejects the formula 11. For, according to the formula 6 this formula implies ∂t/∂z > 0 for all y, which according to Frisch is not realistic, at least not for very small values of y, and perhaps not even for some intervals at larger values.
Next the authors use the formula 7 for the SWF, with
(12) gk = uk1 − ν / (1 − ν)
In the formula 12, ν is an empirical constant with 0<ν<1. This form of gk can not simply be justified theoretically, but it does seem practical. For, firstly one finds for ν→0 the formula 8, with αk = 1. Secondly, ∂gk/∂uk = 1/uν holds. Apparently one finds for ν→1 the formula 9, with ζ
Thanks to the assumptions in the formulas 11 and 12 the welfare function can be calculated. For, suppose that uk = uk(yk) = wk(yk). For the sake of convenience define ρ = 1 − (1−ν) × (1−μ). Then the SWF transforms into
(13) W(y) = Σk=1K yk(1 − ν) × (1 − μ) / ((1 − ν) × (1 − μ)) = Σk=1K yk1 − ρ / (1 − ρ)
According to the formula 13 the marginal welfare is given by ∂W/∂yk = 1 / ykρ. This is the weighing factor, which is coupled to the income changes Δy of the income yk in ΔW. Evidently, in empirical studies the income intervals are used instead of concrete incomes. As an illustration the effect on the SWF is studied for a reduction of the family allowance. The report presents empirical analyses for ρ = 0, 0.27, 0.54 and 1.08. For an optimal W it can make sense to spare the lower incomes when reducing the family allowance. The computations indeed show this, for ρ>0. Nevertheless, the authors warn, that such models can be amenable to manipulation and abuse. Nonetheless, it is exciting to see, that the models in this column really have an immediate practical relevance! The SWF is not purely abstract. In the form of the formula 13 it truly becomes a kind of target function.
The examples in the preceding text show, that there is no obvious choice for a certain SWF. Preferably the SWF combines the virtues of utilitarianism, bargaining, and the low-income policy (and perhaps even more). The SWF embodies the policy, and therefore represents the political relations. The available models are normative, and consequently economists distrust them. In the introductio it has already been stated, that the models are mainly applied with regard to the social structure, such as the question of the income distribution. The analysis of the SWF can give clues about the formulation of the constitution and about the structure of the democratic electoral system. The present paragraph describes a method, where the society as a collective decides about its own welfare function W.
The discussed method has originally been proposed by Rawls. Since the theory of Rawls remains quite abstract, your columnist consults mainly a more practical variant, which has been suggested by the economist K. Binmore in his book Playing fair (in short PF)24. Rawls has revived the concept of the social contract. This looks like a common contract. However, Rawls states that the constitution is a part of the social contract. The constitution formulates morals, values and norms, which are just, and are therefore universally supported by all members of society. A daily convention between all citizens will never be able to agree on a social contract, because everybody will primarily promote his own interests (rent seeking). Now Rawls introduces the idea to place the social convention behind a veil of ignorance.
The veil of ignorance has the effect, that the members of the constitutional deliberations are ignorant about their future positions in society. The members "forget", as it were, their present social position, and shed their professional identity. According to Rawls the ignorance implies, that each member is left with merely his reason (intellect)25. This is a truly bold assumption, because thus each member abandons his or her own identity. Then it is doubtful, whether the construction of the veil still has a practical meaning. Therefore in this regard a heated debate has begun about the degree of transparency of the veil. Binmore presents a more practical variant of the veil. The transparency of the veil is sufficient to observe the status quo of society (p.137, 332 in PF). It merely filters out the social position of each member from his memory26. Therefore he is truly amenable to decisions based on justice.

Binmore has realistic ideas about the morals of the homo sapiens, which he models as a homo economicus (p.22)27. Man tries to defend his enlightened interests (p.148). He depends for his survival on his innate inclination to show empathy for others (p.28, 56). Empathy is the capability to understand, and therefore must not be confused with sympathy28. Empathy is essential for deciding in the constitutional convention about the justice of the social rules. The decisions will succeed, because empathy is partly determined socially (p.63). It has been formed during the social evolution (p.65, 297). The collective convergence of empathy is essential for realizing a social contract! (p.297). Therefore the veil must definitely be transparent for empathy.
According to Binmore, the homo economicus will base his choices on the optimization of utility. So this also happens in the constitutional convention. The formula 8 is applied, where thanks to the empathy the weighing factors αk can be estimated. The αk are the result of an interpersonal comparison, and in fact determine the prevailing social morals (p.88-90). But Binmore also assumes, that the convention leads to bargaining, where the formula 9 is valid29.
Furthermore, Binmore studies the phase after the conclusion of the convention, when the constitution becomes operational. Then all members obtain a social position (perhaps the old one, when the constitution allows this). Therefore their own interest becomes dominant. Binmore promotes for this phase the observation of the constitution. Here Rawls sees no problems, because he supposes, that everybody has agreed to adhere to the rules. The social contract has become a legal matter. But Binmore states, that the homo sapiens is inclined to act opportunistically. Therefore homo sapiens will only adhere to those rules, that are in agreement with his own enlightened interest (p.38, 148). The collective morals must serve the individual, and therefore the morals can never be an absolute dictate (p.129). Morals, which clash with the enlightened self-interest, will be eliminated. Binmore defends this idea with the dissonance theory of psychology.
That is to say, the sound morals are reinforced dynamically in a social process. Cooperation is possible exactly thanks to the enlightened self-interest(p.148)!30 A social evolution occurs, where path-dependent institutions are established (p.130). In this respect Binmore believes in group dynamics, just like Van der Wijk, and in the new institutional economics (NIE). This has consequences for the nature of the social contract. The constitution must be formulated in such a way, that its rules indeed serve the enlightened self-interest. Then the law becomes a self enforcing contract (p.30), or in other words, a self policing state of social consensus. Binmore believes that this is a condition for social stability (equilibrium) (p.34). The social contract is the unanimous choice from the set of available situations of equilibrium31.
Now Binmore wonders, whether during the convention an empathic person will prefer the SWF of utilitarianism, of bargaining, or of the minimax principle (see the figure 2). The members of the convention will realize, that precisely the poor in society will feel a strong urge to infringe the previously agreed rules. The lowest social class is the most revolutionary class. So it must primarily be reconciled with the social contract and with the constitution. Their opportunism is leading. Here Binmore shares the view of Rawls. Therefore the convention will finally choose the SWF of the maximin principle (formula 10) (p.145, 317)32. These are the morals of the modern theory of welfare functions. The reader will not be surprised, that for decades this "unanimous" choice for the maximin principle behind the veil of ignorance has been extremely controversial. The objection is made, that the most wealthy are just as opportunist33.
In the literature, which over the years has been presented in the Gazette, one finds here and there interesting remarks, which place the theory of the SWF in a wider perspective. A part dates already from four years ago, when the welfare function was elaborated for the first time. It is worthwhile to succinctly refer again to a number of these sources. This also makes clear, that the theory of the SWF is criticized in some circles.
The political scientist Herman van Erp states on p.71 in his book Het politiek belang (in short PB)34, that the individualization leads to an increasing pluralism. Since this affects the consensus, the general interest requires more and more, that formal institutions for deliberations are available. Van Erp states that the constitutional convention must weigh the interests, but must ignore the various group morals here (p.88, 94 in PB). The political decisions require consensus about the procedure, so that impasses are avoided (p.100 in PB). Therefore Rawls develops a theory of procedural justice (p.141 in PB). Such a procedure can take into account the intensity of group interests (p.123 in PB). Van Erp states that the obligation in the self-policing contract has a conventional-social character (p.133 in PB).
The constitution protects the citizens against the whims of the democratic parliament (p.226 in PB). The social order can be changed, when certain groups withdraw their support to the prevailing social contract (p.159 in PB). For, then the unanimity has disappeared. Van Erp notes, that such a rebellion plunges the state into a crisis. Precisely for this reason Binmore evidently demands stable contracts. This can be done for instance by establishing institutions for objections and appeals (p.248 in PB). The revolution as an instrument of "emergency law" is philosophically controversial (p.247).
The economist J.J. Graafland doubts on p.154 in his book Economics, ethics and the market (in short EEM)35, that someone can put himself in somebody's shoes. The personal frame of reference can never be completely put off. See also p.165 in EEM. Notably, everybody maintains his identification with his own group (p.167). And the utility experience of animals can not be determined (p.167). In general Graafland rejects utilitarianism (the idea of utility), because the morals are not included in the utility (p.160 in EEM). Consider a moral value such as freedom. Incidentally, some goods and values are mutually incomparable (incommensurable) (p.163). Graafland dislikes in particular the cardinal measurement of utility (p.155 in EEM). The expected utility is difficult to compute, due to the uncertain future. Moreover, the discount of utility can only be determined, when empathy is possible - which Graafland clearly questions 36.
He even objects to the ordinal utility. Some goods can not be replaced (p.164 in EEM). Other preferences are irrational or even immoral (p.164 in EEM). Utility can not be equated to well-being, and certainly not to happiness (p.162 in EEM). Graafland rejects rule utilitarianism (p.168 in EEM). This model first wants to conclude a social contract, which regulates the possible actions - more or less like Binmore proposes. Graafland fears, that the constitutional rules will be undermined, because utilitarianism gives (too) much priority to effectiveness (p.169 in EEM). The reader may see, that various criticisms are conceivable with regard to welfare functions. Some support for the SWF can be found with experiments and statistical data, but this is quite difficult. The social sciences remain highly speculative and subjective, and are subject to personal views on meaning and reason37.
Incidentally, Graafland is positive towards the theory of Rawls. Rawls gives a higher priority to the individual freedom and rights than to material welfare (p.204 in EEM). The constitution can enforce individual rights as a duty for all. Graafland does not mention the model of Binmore, but would undoubtedly reject it because of its foundation in utility and individual preferences.

The economist F.-R. Mahieu refers in his book Éthique économique (in short EE) to the importance of the anthropology for economics38. It is essential to have an accurate image of man, because the economy is socially embedded. Therefore moral quesions enter economics. Mahieu tries to find ways to include morals in economic calculations of utility (p.148 in EE). The utility function of the individual k can be written a suk = u(vk, vs) (p.154, 165 in EE). Here vk is the personal utility, and vs is the social utility, which k assumes thanks to his emphatic feelings (p.136-141 and 163 in EE). In short, one has ∂uk/∂vs ≠ 0. Indeed Harsanyi assumes such a dualistic utility (p.165 in EE)39. On the other hand, Rawls assumes the need for justice (p.155 in EE). Morals are not a priori present, but they can be constructed (p.156 in EE).
Mahieu points out a risk of empathy, namely the psychological trap of the wrong attribution, such as biases (p.172 in EE). They can degenerate into well-meant paternalism. Nevertheless, the social contract sometimes requires an unsollicited intervention and help (p.178 in EE). The collective morals impose the boundaries on the individual utility calculations, for instance by means of redistribution (p.193 in EE). The morals create obligations and rights. However, these also supply the individual with new choice options (p.200 in EE)!40 Consider for instance pension systems. Apparently the utility vs indeed has a substantial influence. As far as the rights are informal, they can never be claimed by law (p.208 in EE). This introduces an individual uncertainty, so at the micro level, which nevertheless can undermine the social stability (p.213 in EE). Here is a source of crises.
Therefore Mahieu warns against the blurring of norms, when the consensus about the social contract has been affected (p.218 in EE). This subject is studied by the public choice theory (p.222 in EE). Citizens tend to probe the boundaries of the constitution. Pressure groups want to extort rents from the state, and sometimes can convince the parliament. Furthermore, communitarians argue, that behind the Rawlsian veil of ignorance the individuals lose their will (p.230-231 in EE). Thus a constitution can never be established. On the other hand, Mahieu objects to the culture idea of communitarianism. For, the group morals are not naturally just or rational (p.236 in EE). The constitutional convention of Rawls and Binmore is precisely introduced in order to escape the subjective dictate by interest groups (p.239 in EE). As soon as the veil is removed, the convention is bound to fail, because then it consists of concrete, egoistic citizens.
In 2003 the Scientific Council for the Government policy (WRR) published the report Waarden, normen en de last van het gedrag41. The main part of this report is devoted to practical measures for reinforcing the social sense of norms, and therefore is of secondary importance for the present column. However, the morals are also analyzed, and this does matter. The report starts from the assumption, that pluriform values and norms are a hallmark of the modern society (p.11, 142, 194). Individuals connect in volatile social networks (197). The civil society remains a healthy breeding ground of pluriform ideas (142). The public morals are formed in practices of citizenship (265). One has to find the minimally necessary communal sense (p.23).
It is easier to obtain consensus about rules and behaviour than about the underlying morals (241). This is evidently precisely the idea of the model of the veil of ignorance. The society itself must create the awareness, which is needed for empathy in the constitutional convention. The citizens must be empowered in order to conserve the constitutional state. The pluriform society requires civilized behaviour in public debates and in public encounters (269). Education, media and integration contribute to the transfer of morals (25). Here the minor virtues can also be learned, such as respect for the truth, empathy and sympathy for others (167). This behaviour is transferred to others as a result of their observation and imitation of the examples (202). The report is sceptical about communitarianism, because conflicts between interest groups must remain possible (152).
Because of pluralism, it is difficult to formulate universal values. The report refers to the ideals of the Enlightenment: belief in the future, personal freedom (autonomy, individualism), reason, universality, justice and equality (12, 146, 244). Solidarity is also recommended on several pages (53, 155)42. It is difficult to prioritize the various values. Often this depends on the situation. The authors do believe, that the institutions must focus more on procedural justice than on distributive justice (259). This idea is also the basis of the theory of Rawls.
The constitution and the principles of the constitutional state guarantee room for diversity and pluriform behaviour, and also offer the possibility to control conflicts (p.36, 38, 148)43. The democratic constitutional state is a stable means for solving the inevitable conflicts of value (56). The constitutional state offers protection and guarantees, also against the majority (155). This is done by means of the constitution and the judge (155). The procedural elements are a value in themselves (156). These are called constitutional norms (p.36). The obliged consensus (in abstracto: the convention behind the veil of ignorance) conserves the values of democracy and the constitutional state and its open character (264). But in the daily interactions the confrontation is of course allowed (38, 65, 121, 171, 191, 220, 266). Next the conflict does need to be solved. Compromises also contribute to bonding (153)44.