
Figure 1: Caricature
Colijn searches majorities
(T. Bottema, 1934)
A previous column has analyzed how public goods can be supplied by private enterprises. There the market regulation was also discussed. The present column uses several of these insights in a model. The first model addresses the political phases of privatizations. The second model shows, how a private enterprise can be controled by means of subsidies. The third model discusses the regulation of a natural monopoly by means of its price structure.
The privatization of the services in the public sector is a policy choice, which originates from a political process. During the eighties of the last century a policy change has occurred, where a new appreciation has emerged for the role of private enterprises, and for free markets, also in the supply of public goods. Many of the changed insights have been included in the new institutional economics (in short NIE), and within it notably the public choice theory. A previous column has sketched a global overview of the present-day ideas. Again and again it is also possible to translate the complex policy processes in a mathematical model. It is true that such models do not increase the knowledge, but thanks to their abstract nature they yet are suited for expressing quite clearly the dominant factors and effects in the policy process.
This column describes three of these models, which incidentally are not at all similar in their contents. They give an impression of the scientific instruments, which are available at the moment for the theoretical policy analysis. The first model concerns the political management and control of social reforms. There is a huge scientific literature about political agenda's and voting procedures. It turns out that in this social choice current the game theory gives fruitful results. The second model shows, how the state can use its financial means in order to influence private enterprises. The third model describes a market regulation by means of price politics, where the general (public) interest and the interest of the private enterprise are reconciled.
The present paragraph mainly consults the book Political economy in macroeconomics (in short PEM)1. The theory notably focuses on the question, how the state can create sufficient support for realizing the privatizations. In this theory the utility of the privatizations is of secondary importance. On the other hand, the utility of the privatizations can not clearly be distinghuished from the approach. Often a privatization leads to groups of winners and losers. In the decision about privatization, the groups will compete for the acquisition of a democratic majority, which supports the interest of the personal group (rent seeking). When then the privatization is poorly handled, it can stagnate halfway due to the blockades, which are put up by the potential losers. In such situations the privatization only becomes a success, when an optimal path is set out2.

In this respect the privatization does not differ from other reforms. The decisions are made democratically, and then the voting procedure can be important for the final result. In particular, the state can determine the agenda, which is used during the path towards privatization. Consider the following example: three equally large groups must together decide about two privatizations (p.638-639 in PEM). In privatization 1 the utility of the groups 1, 2 and 3 equals (u1(1), u2(1), u3(1)) = (1, 1/3, -½). And in privatization 2 the utility for the groups 1, 2 en 3 equals (u1(2), u2(2), u3(2)) = (1, -½, 1/3). When the path proposes the simultaneous privatizations 1 and 2, then the utility is (u1(1+2), u2(1+2), u3(1+2)) = (2, -1/6, -1/6). The outcome for the groups 2 and 3 is negative, and therefore they block the path. The path fails, although the social utility is positive (5/3).
Now suppose, that the state gradually introduces the privatizations. The path is divided in two phases: the privatizations 1 and 2 occur in two successive periods, respectively period 1 and 2. Furthermore, suppose that the groups have a limited time horizon for their decisions, with a duration of 1 period. Then the privatization in period 1 will be supported by the groups 1 and 2, which both experience a positive utility. Next the privatization in the period 2 will be supported by the groups 1 and 3, for the same reason. Note that here the assumption of myopia is essential. For, in the case of an infinite horizon the groups 2 and 3 would see through the approach of the state, and together form a coalition in order to stop both privatizations.
A significant part of the theoretical literature is devoted to ways to overcome the resistance against the privatizations of state enterprises3. A problem of the privatization is, that the sales value of the enterprise is not well known. Sometimes the enterprise will be sold to the direction or to the personnel. But it is also possible to issue shares, and sell them to the public. Or the state enterprise is sold to a single private enterprise. When there is social resistance against the privatization, then it can help to give the concerned citizens vouchers, which represent a share in the ownership of the enterprise. Next the citizens can freely trade their vouchers. The present column will not discuss the policy of the sale of state enterprises any further.
State enterprises have a poor reputation with regard to effectiveness. The book The economics of business enterprise (in short EBE, see footnotes) explains, that it is difficult to incite the direction to perform well. An interesting solution is to establish a mixed enterprise, where both the state and private groups own a package of shares. Thus the state keeps some influence, whereas the private shares make additional incentives possible, such as a performance reward in shares, and extra supervision by the private owners (p.459-460 in EBE). Of old, this approach is popular in Dutch politics, which favours corporatism4. Suppose that the private owners possess a fraction ε of the enterprise. Assume that in the initial situation ε = 0.49 holds, so that the state has just a majority interest.
In previous columns various reasons have been mentioned for keeping the control of the enterprise in the hands of the state. The state (or actually politics) wants to guarantee, that the product is generally accessible, reliable, solidary and durable. Furthermore, the state wants to maintain the employment and the democratic influence in production. Thanks to employment and public influence the politicians can bind the electorat to themselves. Since many consumers do not appreciate this specific employment and influence, the choice for state ownership does not necessarily serve the general interest. Suppose that in an efficient production the wage sum is W. The politics dictates an additional wage sum ΔW to the direction, on top of W, purely for the sake of employment and the increased personal popularity (rent seeking by politicians). This is possible, because it is the main shareholder.
Now suppose that the state chooses in favour of privatization of the enterprise. It sells 0.02 of all shares, so that the private owners obtain a majority interest of ε = 0.51. They naturally want to produce efficiently, with the wage sum W. The state prefers to prevent this by means of a subsidy S to the enterprise. Thus, after privatization the utility function of politics becomes (see p.657 in PEM):
(1) up = α × ΔW − β × (1 − ε) × ΔW − γ × ε × S
The three terms on the right-hand side of the equation have the following meaning. The first term represents the utility of politics due to the increased employment and popularity. The second term is discontent, because the additional expenditure ΔW leads to a lower entrepreneurial profit, and thus to less dividend for the state, Here, 1 − ε is the fraction of the total package of shares, owned by the state. The third term is the dissatisfaction, because the state must pay a subsidy. The dissatisfaction diminishes somewhat, with a factor ε, because a part of the subsidy returns to the state in the form of profit. Therefore the "nett" subsidy is ε×S. The constants α, β and γ are simply conversion-factors, which transform the money sums into the subjectively experienced utility.

The direction defends the interest of the private shareholders, and therefore maximizes the profit. The private owners obtain a fraction ε of the profit. Therefore the utility function of the direction is:
(2) ud = ε × (S − ΔW)
The direction and politics will begin to bargain in order to determine the size S of the subsidy. First, note that S > ΔW is required for an agreement. For, when ud threatens to become negative, then the direction will prefer S = ΔW = 0. This would imply a restructuring, where the superfluous personnel ΔW will be dismissed. The negotiation is described as an optimization problem:
(3) maximize for all possible S: up × ud
The model in the formula 3 implies, that politics and the direction have an equal bargaining power. The optimum of the problem is called the Nash solution. It is (p.658 in PEM):5
(4) S = (α − β × (1 − ε) + γ × ε) × ΔW / (2 × γ × ε)
The formula 4 naturally leads to the question, whether this optimum is realizable in the negotiations. The demand S > ΔW in combination with the formula 4 makes clear, that an agreement must satisfy the inequality:
(5) α > β × (1 − ε) + γ × ε
A large α implies, that politics is really eager. This simplifies the bargaining process. Besides, the formula 5 allows to make conclusions for the case β<γ. Then in the right-hand member the factor (γ − β) × ε is positive. Suppose that the state decides to diminish its package of shares further. Then ε will rise, so that perhaps the formula 5 can no longer be satisfied6. An agreement will no longer be possible, so that subsequently the direction will reduce the number of jobs.
The privatization of a state enterprise is often accompanied by a restructuring of the concerned market. For, a private enterprise reacts to other incentives than the state, and notably aims at the maximization of the profit rate. Precisely for this reasons a century ago it became popular to bring the natural monopolies in state ownership. In such branches there are commonly large fixed costs, for instance because at the start a personal conduit network must be constructed (public utilities such as water, gas, electricity, cable TV, and transport by rail). A private monopoly would push up the product price at will. This hurts the general interest. The state can not really prevent this.
One would think, that in this situation a price policy is a solution. But the problem of private production is, that the state has even less access to the production information than in the case of state enterprises. In other words, the state must make high costs in order to be able to judge the private price policy. The measuring costs (information costs) are huge. However, during the seventies of the last century new insights emerged, which are less pessimistic about the control of private monopolies. Policy constructions were designed in order to regulate the monopoly market. The new ideas did not completely solve the measuring problem, but they did show, that the state yet can somewhat impose its will on private monopolies, even with limited and incomplete information. For instance, the Dutch electricity branch functions well after privatization7.
As an illustration of the new insights the present paragraph will describe a model of market regulation of the natural monopoly8. Suppose that the state wants to control the monopoly by imposing a price structure on the market, which consists of a fixed tariff T and a piece price p. The price policy must reconcile the private interest of the enterprise with the general interest. Now the model analyzes the information problem, albeit for a simple and not very realistic situation. For, the state knows the fixed costs CF, but not the piece costs c. The state does know, that the piece costs cL occur with a probability π and cH with a probability 1 − π (where one has cL < cH). It is obvious that the piece price p and the fixed tariff T will depend on c, and therefore they can assume two values, namely the combinations (TL, pL) and (TH, pH).
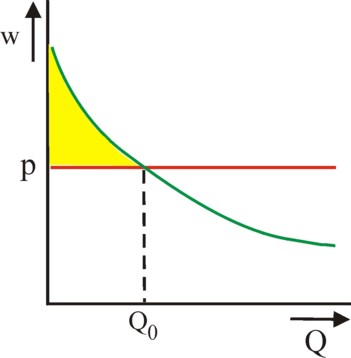
The state translates the general interest in a target function u. The choice for the form of u is subjective (political). A popular choice is to maximize the so-called consumer surplus S (in the German language Rente). Let w(q) be the piece value according to an average consumer. This represents the demand curve V on the market, and is falling due the the decreasing marginal utility of a product unit (∂w/∂q <0). The consumer will buy precisely so many pieces qo, that w equals the product price p. Therefore the consumer actually acquires a surplus with a size of9
(6) S = ∫0qo (w − p) dq
In the figure 3 the consumer surplus is represented by the yellow area. Since qo depends on p, this definition shows, that S depends on p. However, the maximization of S alone does not suffice, because the general interest also requires, that T is not extremely high. Thus it seems logical, that the state prefers the target function10
(7) u = π × (S(pL) − TL) + (1 − π) × (S(pH) − TH)
The profit of the private produces is given by the difference of the sales and the costs
(8) φ = p(c) × q + T(c) − (c × q + CF)
It is obvious that the enterprise will only produce, as long as φ≥0 holds. This is called the participation condition. The enterprise always has a reservation-profit of 0. It has already been remarked, that here the measuring problem of the state is, that c can not be observed. Therefore the enterprise can increase its profit by proclaiming a false c. In the framework of the present model, the enterprise states that it has costs cL, even when they are actually cH, as long as one has φ(pL, TL) > φ(pH, TH). And it proclaims cH, when the inequality is the reverse. In this situation the state is forced to design a self-enforcing contract11. Conditions of encouragement are added to the contract, namely
(9a) (pL − cL) × q(pL) + TL ≥ (pH − cL) × q(pH) + TH for the case of true costs cL, and
(9b) (pH − cH) × q(pH) + TH ≥ (pL − cH) × q(pL) + TL for the case of true costs cH
It is clear from the formula 8, that the formula 9a equals φ − CF, for the case that the costs are cL. In the left-hand side the enterprise proclaims true costs cL, and in the right-hand side it proclaims false costs cH. Thanks to this condition the enterprise is incited to tell the truth. The formula 9b applies to true costs cH, and also guarantees that the enterprise will prefer the truth. The optimization problem of the state is thus the optimization of the target function u in the formula 7, by an appropriate choice of (TL, pL) and (TH, pH), with as accompanying conditions the formulas 8 and 9a-b.
In principle the formula 8 has two accompanying conditions, namely with cL and cH. However, when the accompanying condition holds for cH, then it turns out that the condition for cL is automatically satisfied12. Therefore the profit condition in the formula 8 merely expresses a limitation for the case with cH. Furthermore, note that it is true that the set 9a-b is necessary, but not both at the same time. However, for the moment it can not be determined, which of the two (9a or 9b) can be left out13. The thus formulated optimization task is called a Lagrangian problem. The optimal solution for a Lagrangian problem with inequalities as accompanying conditions is found by applying the so-called Kuhn-Tucker theorem. All these preceding statements can be summarized in a Lagrangian L of the form
(10) L = u(TL, pL, TH, pH) + λ × [pH × q(pH) + TH − (cH × q(pH) + CF)] + μ × [(pL − cL) × q(pL) + TL − ((pH − cL) × q(pH) + TH)] + ν × [(pH − cH) × q(pH) + TH − ((pL − cH) × q(pL) + TL)]
The parameters λ, μ and ν in the formula 10 are called the multipliers of Lagrange, and they must not be negative in this situation. According to the Kuhn-Tucker theorem the derivatives of L with regard to TL, pL, TH and pH must all equal zero. When these 4 differential equations are written out, then it turns out that the optimum is14
(11a) TL = (cH − cL) × q(pH) + CF
(11b) pL = cL
(11c) TH = π × (cH − cL) × q(pH) / (π − 1) + CF
(11d) pH = cH + π × (cH − cL) / (1 − π)
Apparently the self-enforcing contract requires, that TL > TH and pL < pH hold. When the formulas 11a-b-c-d are inserted in the formula 8, then one finds the profits φL = (cH − cL) × q(pH) and φH = 0. The encouragement conditions guarantee, that the private monopoly always reveals her true costs to the state. Lying does not lead to a higher profit. On the other hand, apparently this contract can not prevent, that in the situation with cL the monopoly succeeds in making a profit. The reason for this profit, which is called the information rent, is as follows. Since the state aims to realize a large consumer surplus, also for cL, it wants to keep pL relatively low. The monopoly must be compensated for this, namely by allowing a high fixed tariff TL (with a value above CF). On the other hand, in the situation with cH the piece price is above the piece costs. Since TH < CF, it nevertheless turns out that in this situation the monopoly just does not receive a rent.
In reality the situation of the model will naturally never occur. It is too simple for that. The model merely serves as an illustration, that the state or its supervising agency can often moderate the profit motive of the private enterprise. Even in the case of incomplete information, rules of thumb for the operation and a healthy mind can be sufficient to impose an effective regulation. The model shows, that this even succeeds in the extremely unfavourable case of a natural monopoly.