
Figure 1: poster NVV
For a long time it was believed that a hierarchy is very suited for executing policies. However, the principal-agent model has created doubts about this belief. The present column presents an extensive explanation of this model, which has led to a revaluation of market operations, also in the public sector. Behavioural economics suggests several improvements. Finally, the mathematical model is described in detail, at least for the case of the unobservable effort of the agent.
Suppose that each individual is in principle completely free to dispose of himself. Then the question arises, why people nevertheless submit to an external authority. The sociologist J.S. Coleman attempts to give an answer in his book Foundations of social theory1. The remainder of this paragraph is mainly based on his findings. Coleman presents the submission to authority as a mutual exchange. This exchange resembles the exchange on the commercial market, but no price can be attached to the submission. Therefore Coleman calls this a social exchange. The submission to an authority equals the waiving of serveral rights, that are in principle an individual property. They are a part of the original means and richess of that individual. The individual will only waive these means, when he or she gets something in return.
The individual who submits is called the agent. The individual who acquires authority is called the principal. Coleman considers the exchange both from the standpoint of the agent and the principal. In the simplest case, somebody will become an agent, simply because a reward is offered as a compensation. That compensation is required, because the intrinsic motivation of the agent for the activities, that must be done, is insufficient. Coleman calls this situation a disjoint authority, because the interests of the agent and the principal do not naturally coincide. In many respects their interests are even conflicting, sometimes to such an extent, that they cause a latent social conflict, such as the marxist class struggle (see p.81). But in any case the exchange more or less guarantees the existence of the agent.

Next Coleman states, that the principal benefits from the exchange, because the authority gives him access to the efforts and skills of the agent. This observation makes clear, that a second relation of authority is conceivable, besides the job. Namely, a groups of individuals can decide to submit to the authority of a very capable person. Then the group expects that this group representative better defends their interests than each group member could do for himself. Coleman calls this a unilateral exchange, because the group members do not get anything in return for waiving their rights, except the hope for a better furthering of interests. It is remarkable that in this case the group members are still the principal, because they retain the ultimate right to dismiss their representative. The representative is an agent.
The best known example of the unilateral exchange is the election of a democratic parliament. Then it is true that the people remain the final sovereign, but it delegates its rule to the professional politicians. Coleman calls this situation a conjoint authority. Moreover, this example illustrates the feedback in the social system. For, the politicians appoint an administration, which subsequently hires citizens in order to execute its policy. Therefore the citizens, who first place the politicians in the position of a principal, become the agents of the politicians. Indeed, according to Coleman the functioning of the social system must be explained from the individual behaviour at the micro-level (in this case the elections and the applications)2.
The use of authority commonly affects the interests of some individuals. Therefore authority must always rely on some form of power. In politics the power begins, when citizens identify with their leaders, and it ends with the social legislation and regulation (sanctions). Coleman stresses the importance of dedication or love (see p.76, as well as p.157 and further), which is also dominantly present in the social model of the Dutch economist Frijters. It originates from the personal psychology. However, yet power is commonly based on the social contract, which citizens conclude rationally as a self-commitment. Hereafter only two exit options remain: the administration can be dismissed by the voters, or the individual can emigrate. Power is a phenomenon at the macro level, because it expresses the measure, in which an interest can assert itself in the social system (p.133).
The principal-agent model is invented in order to study the effectiveness of authority. For, the interests of the agent and the principal commonly do not coincide completely. Then the principal faces the problem to optimally motivate the agent. Here the principal is hindered by two factors. Firstly, the future is uncertain, as far as the developments are beyond his authority. That makes the results of his management somewhat unpredictable. And secondly, the agent disposes of information, that remains hidden for the principal. The information is distributed asymmetrically. That gives an expert power to the agent, which he can use for his own benefit. Economists just started to reflect on this matter during the seventies, when it became clear that the economic planning by the state does not yield the expected positive results.
At the time it became clear, that the state can not be considered as a neutral body in the hands of the sovereign people3. And that has serious consequences for the soundness of the various political doctrines. Notably a more critical attitude has formed with regard to the many state interventions. In many cases, on reflection the operation of markets is yet preferred. First, the political rule can degenerate into an autocracy, which develops her policy according to her own interests. Second, the administrative bodies, that must execute the political policy, can also further their own interests. Science has replaced the traditional view of the administrative servitude and ethics by a model, where also the officials act as egoists. The producer in the state sector has the same urges as the producer on the private markets4.

Already around 1960 the so-called Public choice school develops a theory, that stresses the opportunism of the officials. Politicians and officials try to structure the economic system in such a way, that they can extract a maximal rent for themselves. That undermines the targets, that have been dictated to these two executive layers by the people as the sovereign principal5. It is obvious that before there had also been doubts about the good intentions of the state, but they have really become concrete during the last half of the century. Cusin and D. Benamouzig in their book Économie et sociologie even perceive a crisis of legitimacy of the state6. Therefore state-oriented ideologies, such as the social-democracy and corporatism, lose credibility7. Henceforth, the state is preferably again placed at some distance from the economy, that is to say, economically he becomes less active.
Radically-left circles have the tendency to call the public choice theory neoliberal, which is meant to be denigrating. However, loyal readers remember that the former marxists W. Brus and K. Laski also apply the principal-agent model, namely in order to analyze the failing of the Leninist planning8. These authors state, that in a Leninist system all directors of enterprises are state servants, so that in the principal-agent problem they have the role of subordinates. They can always shift their entrepreneurial risks towards the state, and that is a moral hazard. According to the minimax principle the enterprises try to reduce the planned output, and to increase the allocation of production factors. That makes the production costs uncontrollable. Thus the Leninist planning is even a textbook case of the principal-agent problem.
In the west the planning was commonly indicative, although half a century ago the social-democracy wanted to exert yet more state coercion9. Nowadays Frijters and others even state, that the private markets are among the staunchest defenders of democracy10. According as this idea becomes common, it is applied more often in democratic processes. The execution of the political policy is also modernized, and this evolution is still in progress. On p.366 in Économie et sociologie this is called new public management. When possible, the private sector is brought in for executing the policy. On the global markets the enterprises are so large, that they can make enormous investments, for instance in constructing infrastructure and subsequently exploiting it. The hierarchy is replaced by contracts. The state does continue to cover the risks, that can not be borne by the citizens or enterprises (p.370)11.
It will be clear that during the last decades a preference has grown for supplying public services by means of the private markets. For, on a free market the supplier must compete with other suppliers in order to gain the favour of consumers and customers. Then those suppliers, that try to appropriate surplus value at the cost of the consumer, are simply expelled from the market. Thus the operation of markets has the effect, that the public services become more efficient, cheaper and qualitatively better. This does not at all imply, that in the commercial sector the principal-agent problem is absent. However, it remains within bounds due to the discipline of the market.
It is interesting, that the principal-agent model is not just a qualitative argument. It has initiated the development of the so-called contract theories. In such theories truly quantitative calculations are performed for finding the most efficient manner of controlling the agent. In principle this is obviously a gigantic research area. However, the attention is focussed on two problems, which have just been mentioned. Firstly, the principal sometimes disposes of more knowledge about the effectiveness of the activities than the agent. This is also a form of asymmetric information. The principal can use his preponderance in knowledge for manipulating the agent. On the other hand, the agent knows better than the principal the required effort for executing the activities. In that case the agent will raise his own income by exaggerating the efforts.
Both types of manipulation have been studied in detail. However, the present column is limited to the second problem, of the bartering agent.
Although the principal-agent model gives a description of all kinds of complicated group behaviour, it simply applies the image of man as a rational, egoistic homo economicus. Therefore the contract theories mainly analyze the material incitations, the so-called income motive. However, since several decades happiness economics and behavioural economics have shown, that in many cases the individuals act irrationally. Therefore especially behavioural economics is critical towards the principal-agent model, at least in its standard form. The present paragraph succinctly explains this. It must immediately be noted, that the foundations of the principal-agent model are not questioned. But refinements and nuances are added.
The American economist N. Wilkinson gives in An introduction to behavioral economics an interesting example of the situation in the principal-agent model12. It concerns an enterprise, that wants to incite its agent to make a maximal sales effort. Suppose that the agent makes an effort e, with values between 1 and 10. He experiences this effort as a burden. Assume in the footsteps of Sam de Wolff, that his displeasure is quadratic in e:
(1) c(e) = ¼ × (e − 1)²
In the formula 1, the displeasure is represented by a money sum c. The agent receives a wage w of the enterprise, and therefore must generate at least e=1. The (money-)utility of the agent is u = w − c. The enterprise receives for each generated unit of e a sum pe = 10.
Both the entrepreneur (principal) and the salesman (agent) try to maximize their utility. For the enterprise that goal is commonly simplified by assuming profit maximization. When in the economy all information would be completely available, then the enterprise would reward its salesman according to at most his marginal product. It can not pay more to a worker than his productive value. In this case the marginal product is constant, namely pe = 10. The marginal costs for the salesman are ∂c/∂e = ½×(e − 1), so rising with e. Even at the maximal effort e=10, ∂c/∂e is merely 4.5. Apparently both the enterprise and the salesman benefit from yielding the maximal effort. Then the enterprise receives 100 as the outcome of sales, and the salesman has a displeasure of 81/4, so approximately 20. The wage is determined by bargaining, and must lie between 81/4 and 100, since the utility u is not negative.
However, the situation changes, as soon as the enterprise can not verify the effort e. For, then the salesman is tempted to cash his wage of minimally 81/4, and make an effort of for instance merely e=1. Then he does not experience displeasure, whereas on the other hand the enterprise would suffer a loss. The English expression for this opportunism is shirking. It would seem, that the enterprise can estimate e by means of its sales. However, the principal-agent model assumes that the economy is dynamic. The market processes create fluctuations in both the price pe and the sales, even when the sales effort e does not change. Therefore the sales is not a reliable measure for e. So the enterprise must try to motivate the agent to make an optimal effort. Motivation can be realized by means of supervision and coercion, or by means of performance rewards.
For the case with supervision and coercion, Wilkinson assumes that this causes costs K. Especially when a large effort e is required, the supervision will be complicated. Thus K(e) is a rising function, for instance K(e) = 17/12 × (e − 1)². Thus for the case of coercion the profit π of the enterprise is given by
(2) π = 10×e − w − K
The maximization of the profit requires that ∂π/∂e = 0 holds. From this, it can immediately be calculated, that the maximal profit is realized for ec=4. The contract of the salesman obliges him to make this effort ec. Then, according to the formula 1 his displeasure is c=9/4. The entrepreneur will offer the wage w=c, because then the displeasure is exactly compensated (u=0).
A common manner to enforce the effort ec is sanctioning with a fine F, when the goal is not attained13. When the performance is less than ec, the wage of the salesman is reduced with the fine F. The fine must ensure, that shirking is not rewarded. In the worst case the salesman would choose e=1, resulting in c=0. That equates his utility to u=w. The fine must make this utility negative, meaning that u = (w − F) <0. That can be done for instance with F=2.5. Thus the contract is completed. However, it is clear that the asymmetric information has a devastating influence on the welfare of both the enterprise and the salesman. Whereas with full information the profit can be maximally roughly 80, here it is merely 40 − 9/4 − 51/4 = 25. This obviously also limits the potential wage offers.
Now consider the alternative form of motivation. For the situation with a performance reward Wilkinson assumes, that the enterprise promises an extra bonus b to the salesman. The utility of the salesman becomes u = w + b − c, and the enterprise obtains a profit
(3) π = 10×e − w − b
The enterprise hopes that the salesman will appreciate the bonus, and will show his gratitude by making a maximal effort. This is the principle of reciprocity. In a previous column w+b is called the efficiency wage, because the contract becomes self-enforcing. However, this does not fit with the common economic image of man. For, the homo economicus is not grateful, and will still shirk. Moreover, this way of motivating fails, because according to the contract the bonus is paid only after the completion of the performance. Now the salesman believes, that the entrepreneur will not fulfil his promise. For, he is also a homo economicus, which is not grateful. Thus the salesman will still prefer e=1. The entrepreneur realizes this, and offers w=0 and b=0. The final result is u=0, and π=10. This is even worse than the situation with coercion.
Wilkinson presents this argument in order to illustrate that the standard economic model gives unrealistic results. For, in practice the industries do use efficiency wages. Wilkinson also cites a laboratory experiment, where it turns out that the concerned persons have a clear preference for offering contracts with a performance reward, instead of contracts with coercion. Then both the entrepreneur and the salesman attain a higher welfare. The causes are the feelings of reciprocity, good working morals, and a dislike of inequality. The homo economicus in the standard model is simply unrealistic.
The American economist E. Cartwright comes in Behavioral economics to similar conclusions as Wilkinson14. Behavioural economics shows, that in principle people dislike inequality. It is experienced as an injustice. However, Cartwright stresses that the intentions or aims, that motivate the individual actions, are also important. It turns out that individuals are more positive about inequality, when it is inevitable or normal. So there is little aversion against an enterprise, that is forced to reduce the wages, or to raise its product prices. Now it is not simple to convince people that a measure is inevitable. Therefore entrepreneurs tend to be reserved with regard to lowering wages or raising their prices. Cartwright uses this to explain the well-known rigidity of the wage- and price-level15.
Conversely, also Cartright states, that the payment of bonuses stimulates the performances of the workers (agents). Paying wages with a structural excess above the wages of comparable enterprises is also an incitation to perform. Cartwright cites various laboratory experiments, which confirm this. Unfortunately, in both situations the phenomenon of preference drift occurs, when the agents get used to the bonus or the higher wage. Then they can only be motivated once more by again raising the bonus or the wage. Nevertheless, this form of motivating is often used.
Such qualitative arguments about the movitation of agents are in itself known for many years. Behavioural economics is interesting, because it tries to develop quantitative models of motivation. Namely, these can be used in an attempt to concretely calculate the effect of performance contracts. Thus Cartwright refers to the reciprocity model van Rabin, which has already been described in a previous column, based on the book of Wilkinson16. The utility formula from that column is repeated here, in a slightly modified form
(4) u(SA, SB, S'A) = XA(SA, SB) + α × f(SA, SB) × g(SB, S'A)
The formula 4 describes an interaction between two individuals A and B. Each individual I (with I=A or B) applies a strategy SI, and thus realizes a material outcome XI. The strategy S'A is the strategy, which according to A is expected by the individual B. The function u is the utility, which the individual A acquires due to the interaction. The function f is the altruism- or kindness-function of A. The function g is the altruism- or kindness-function of B, that is expected by A. The functions are positive for altruistic individuals. The constant α expresses the inclination of the individual A to prefer reciprocity. A homo economicus lacks this inclination, and therefore has α=0. However, a true human being enjoys reciprocity (f), and even more when she is returned (g). Conversely, a scorned altruism (f>0, g<0) causes feelings of displeasure and aversion.
The formula 4 is merely empirical, and not based on profound theories. It is quite clear, the A tries to model the intentions of B by means of the functions f and g. Now Cartwright applies the formula 4 to the situation of an entrepreneur B and his salesman A. The salesman must decide, whether he will raise his level of effort with a quantity Δe. In the state L (low) he fails to do so. In the state H (high) he makes the extra effort, and thus generates an extra product yield of ΔR. However, that effort costs him an extra disutility of Δc. It is logical, that A expects a bonus for his extra effort Δe. Cartwright asks what defines a reasonable bonus. The entrepreneur B obtains an extra yield of 0 or ΔR, depending on the decision of A. It makes some sense to suggest, that A is just, when he produces the average ΔR/2 of these two extremes. For, moderation is commendable.
In that way A concludes that he is kind, when he chooses the situation H with the effort Δe. For, then B obtains an extra yield ΔR, and that is ΔR/2 more than what is just. Apparently the altruism function could be represented by f = -ΔR/2 in the situation L, and f = ΔR/2 in the situation H. In the situation H, A must obviously get a bonus, because he makes the extra effort Δe. It is just that the entrepreneur shares his extra yield ΔR with A, and gives him ΔR/2. Any bonus larger than ΔR/2 is kind of B. Apparently the kindness of B is measured by b − ΔR/2. In other words, the altruism function of B could be represented by g = b − ΔR/2.
Now the mentioned findings can be inserted in the formula 4. One finds
(5a) u = b − α × ΔR/2 × (b − ΔR/2) in the situation L, and
(5b) u = b − Δc + α × ΔR/2 × (b − ΔR/2) in the situation H
The set 5a-b is fascinating. For instance, it is clear that the choice for the situation L is frustrating for A, when he receives a generous bonus in return. Yet a kind bonus b>ΔR/2 can not guarantee, that A will always prefer the situation H. For, A has the disutility Δc, that must be compensated. The formula 5 shows, that his compensation is realized only, when one has
(6) b > ΔR/2 + Δc / (α×ΔR)
Precisely the disutility Δc brings about, that ΔR/2 is yet not a just bonus. In the situation H the entrepreneur B can pay at most a bonus of b=ΔR, and preferably less. Due to the formula 6, the requirement b<ΔR implies, that Δc < ½ × α × (ΔR)² must hold. In other words, as long as the disutility of A is not too large, B will be willing to pay a bonus b, which motivates the salesman A to choose the situation H. Here the inclination of reciprocity α of A is also essential, a fact that passes unnoticed in the standard economic model, due to its image of man, the homo economicus.
Now that the principal-agent model has been modified with several nuances from behavioural economics, next the general model can be described, as it is applied in the standard economical theory. It ignores the irrational behaviour, such as reciprocity or an aversion of inequality. The model does take into account the human inclination to be averse to risks. This implies concretely, that individuals prefer a guaranteed sum of money over an uncertain expectation of a slightly larger sum. This property is actually the backbone of the model. The present paragraph is based on the explanation in the book Microeconomic theory, where regular comparisons are made with the somewhat different discussion in the book Labor economics17. This comparison is mainly relegated to the footnotes.
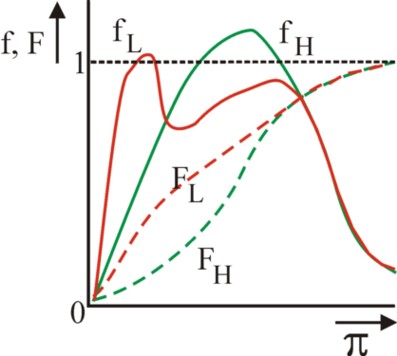
Meanwhile the reader knows, that asymmetric information such as an unobservable and non-verifiable effort leads to a moral hazard. The effort e of the agent becomes unobservable for the principal, when he can not exert a complete supervision18. It has been explained previously, that then the principal must provide the labour-contract with incitations to make a maximal effort. In the studied situation the principal is again an enterprise, whereas the agent is a salesman. This type of models is dynamic, because the yield of the enterprise depends on market fluctuations. In Microeconomic theory this is modelled by assuming that the profit π occurs according to a density function f(π|e). That is to say, for a given effort e the profit π can be expected with a probability density f 19. The possible values of the profit lie in interval [πmin, πmax].
Thus the chance that the profit is less than π is given by the distribution function
(7) F(π|e) = ∫πminπ f(χ|e) dχ
The figure 3 sketches the density- and distribution-function for two efforts eL and eH. It has just been said, that such models introduce a risk in the profit π. This type of models commonly assumes, that the principal is risk-neutral. He is so rich, that the various risks in his portfolio or investment-package roughly compensate. As a formula this is expressed by ψ(E[π]) = E[ψ(π)], where ψ is the utility function of the principal. The function E(x) measures the expected value of x, and is defined as
(8) E[π] = ∫πminπmax χ × f(χ|e) dχ
In a previous column about risky incomes it is shown that for a risk-neutral individual the money utility ψ(π) is proportional to the money sum π. Therefore the profit maximization is also the utility maximization. Incidentally, the present definition of the profit will make the somewhat unusual assumption, that it still contains the wage w of the agent. In Microeconomic theory the additional assumption is made, that the effort of the agent can take on merely two values, namely eL and eH, with eL<eH (Labor economics does not use this simplification).
The utility function of the salesman is20
(9) u(e, w) = v(w) − c(e)
This utility function has a more general form than previously in this column. The utility of the wage w is measured by the utility function v(w), and now c(e) is also a true utility function (and not the money value of utility, like before). The agent also takes a risk, because in principle his wage w(π) depends on the profit. He is not necessarily risk-neutral, because for him the wage is his only source of income. His portfolio is not diverse. Henceforth your columnist assumes, that the agent is risk-averse. In that case v must satisfy ∂v/∂w > 0 and ∂²v/∂w² < 0, that is to say, v has a concave form. Furthermore, suppose that besides the offered contract the agent disposes of an alternative, with a reservation-utility level U. Then the contract must satisfy the participation condition E[u(e, w)] ≥ U. It is commonly assumed that the agent will even accept the contract, when E[u] equals U.
The case with an observable effort
First, consider the hypothetical case, that the effort would be observable. Then apparently the redaction of the optimal contract by the principal can be represented by an attempt at maximizing
(10a) maximize for all e and w: E[π − w(π)]
(10b) under the participation condition E[v] − c(e) ≥ U
Note that in the formula 10b use is made of the formula 9 and of E[c] = c. It turns out to be convenient to first choose the optimal w(π) for a yet to be determined e. Then the maximization of the formula 10a changes into the minimization of E[w}. This type of problems can be solved with the method of Lagrange, resulting in21
(11) ∂v/∂w = 1/λ
In the formula 11, λ is a constant. Since for risk-aversion the derivative ∂v/∂w is a falling function of w (due to ∂(∂v/∂w)/∂w <0), just one value of w can solve the formula 11 22. Apparently w(e) is independent of the arbitrary value of the profit π(e). The principal fully insures the agent against the fluctuations of the profit, as it were. The principal does not want to pay too much to the agent, and in the condition 10b takes the lower boundary. Let v-1 be the inverse function of v, then for the principal the optimal wage is w(e) = v-1(c(e) + U). Furthermore, now E[w]=w holds. Finally, the principal must choose between the two situations with efforts eL and eH. In short, the optimization problem 10a-b of the principal is simplified into
(12) choose the largest of E[π(eL)] − v-1(c(eL) + U) and E[π(eH)] − v-1(c(eH) + U)
After this detour the argument returns to the case with the unobservable effort. Contrary to the set 10a-b, now the principal can no longer directly dictate e. He can merely minimize the wage w(π). The set 10a-b does inform him about the effort eo, that is optimal for him. Then he can design the contract in such a way, that it incites his agent to make this desired effort eo. This can be guaranteed by adding the so-called incentive constraint to the set 10a-b. It states:23
(13) eo must yield the maximum of E[v(w)] − c(e)
Suppose again that the principal can choose between eL and eH. When he accepts eo = eL, then he can act in the same manner as with an observable effort. He simply offers the wage w(eL) = v-1(c(eL) + U). For, then the participation condition is satisfied, so that the agent will accept the contract. And the principal will naturally prefer eL.

An even more interesting case is obtained, when the principal tries to seduce his agent to do eH. The incentive constraint in the formula 13 shows that one must have: E[v(w(eL))] − c(eL) ≤ E[v(w(eH))] − c(eH). When here the identity holds, then apparently the assumption is that the agent yet prefers eH. The Kuhn-Tucker theorem states that the studied optimization problem yields the relation25
(14) 1/(∂v/∂w) = λ + μ ×(1 − f(π|eL) / f(π|eH))
The similarity wit the formula 11 is clear. It can simply be shown that λ and μ are both positive26. The principal can use the formula 14 for calculating the wage function w(π), that incites the agent to choose eH.
Since f(π|eL) / f(π|eH) can assume both values as a function of π, apparently ∂v/∂w can behave rather capriciously as a function of π. But it has been shown previously that ∂v/∂w is a falling function of w. The conclusion must be, that w(π) can behave capriciously as a function of π. The contract can in some intervals of π offer a lower wage, when the profit rises. See for instance the figure 4, which is copied from p.486 in Microeconomic theory. The cause is obviously, that f(π|e) models the capriciousness of the market. The market can push up the profit, even when the agent makes little effort, and conversely. This is an important finding of the whole previous argument.
A second finding also deserves mentioning. Namely, the participation condition implies E[v|eH] = c(eH) + U. Furthermore, a previous column shows, that risk aversion of the agent leads to E[v(w)] < v(E[w]). Now, v is a strictly rising function, so that the same holds for v-1. This has the consequence, that E[w] > v-1(E[v(w)]) holds. In short, it turns out that E[w|eH] > v-1(c(eH) + U) holds. And the right-hand side of the inequality precisely equals w(eH) for the case of an observable effort.
Apparently, in the situation with an unobservable effort eH the expected wage of the agent is higher than in the situation with an observable effort eH. In the situation with effort eH the wage rise is needed in order to insure the agent against the risk. His experienced utility is equal for observable and unobservable efforts, namely U. But these extra costs for the situation eH reduce the income of the principal. It has just been concluded, that the situation with eL does not have this problem. Thus it is conceivable, that sometimes the principal actually would prefer the effort eH, but that due to the costs of the risk insurance finally the effort eL is still cheaper for him. Apparently the unobservable effort leads to a loss of welfare for the principal, and thus for the society as a whole. This is the most important conclusion of the principal-agent model with unobservable effort27.