Figure 1: Marginal utility (Gossen, van Praag)
Since about a century the economic theory is dominated by the paradigm of the marginal utility, which has been discovered first by H.H. Gossen, in 1854. A disadvantage of such a dominant position of a paradigm is, that she is gradually beaten down into a dogma. Each textbook contains the same phrases, and a reasonable discussion is hardly possible any more. This column presents two original thinkers about the marginal utility, namely the Leninist economist K.K. Val'tukh (with thanks to the second-hand bookshop Hofbuchhandlung in the German Löwenberg), and the Dutch economist B.M.S. van Praag.
The real economy must aim to maximize the welfare, given the available production factors. The economic science wants to support her in this endeavour. This generally accepted fact is perhaps best formulated in the fundamental economic law of Leninism1
The ultimate policy target is the growing satisfaction of the increasing material and cultural needs of the people, by means of a continuous development and improvement of the social production
Often the remark is added, that these needs arise from the unfolding of the human personality and of the social relations.
The welfare is measured by means of the quantity of useful goods and services, which are made available to the population. The individual man (or the separate household) tries within his budget to buy the combination of goods and services, which yields the maximal utility. In other words, the individual maximizes his utility2. Therefore economics has always, and certainly within the last century, tried to identify the shape of the utility functions of individuals. A knowledge of the utility functions is indispensable, both in the analysis of the state policy and in the operation of free markets.
This column wants to give some insight in the behaviour of utility functions. In a previous column the approach has already been described, which was used by Jacob van der Wijk for the determination of the important marginal utility of money. This concerns the marginal utility, which stems in a natural manner from the social conditions. Recently the economist Bernard van Praag has also determined the marginal utility for the individual (casu quo the separate household). His findings form the core of the present column.
Van Praag finds results, which confirm the suspicion of Van der Wijk, that the marginal utility of money is to a large extent determined by the society. That is to say, the marginal utility is a social phenomenon, and fixed neither at the purely individual level nor in a natural and universal manner. Van Praag develops a vision about the marginal utility, which has a striking similarity with the ideas of the economists in the former Leninist states. Therefore in this column many citations will be found from a work3 of K.K. Val'tukh (in the German language Waltuch), at the time a leading Leninist economist with regard to the theory of utility. Little attention will be paid to the conventional vision about the marginal utility. She can be found in any introductory textbook.
Before starting the thorough analysis of the theory it must be remarked, that the human needs are actually not satisfied by products (in casu goods and services). In reality the individual desires properties of products. For instance a person loves the taste of sweet, but not necessarily cane sugar, beet sugar or sorbitol. Or someone needs light, so a light-bulb, but not necessarily an economical bulb. Perhaps even a candle will suffice. Therefore Van Praag concludes, that the need focuses on a quality aspect, that can be satisfied by various products4. Val'tukh also decouples the need from a concrete product5. Incidentally in the present column the difference between the aspect and the product is not important.
The paradigm of the marginal utility starts with the supposition, that n goods and services are supplied on the market(s). An individual (or household, which in the present context amounts to the same thing) disposes of a certain budget or income, which can be spent on the acquisition of products. It may decide to buy for instance quantities xj of each product j. When the total combination of quantities x1, ... , xn of products is represented by a vector x, then the individual utility function attaches the value u(x) to the utility of the chosen combination. Gossen has used this notion of things as the starting point for the development of his theory.
His first law pertains to just one product. It states:
The intensity of a need decreases when it is satisfied more and more, and can even become negative past the point of saturation.
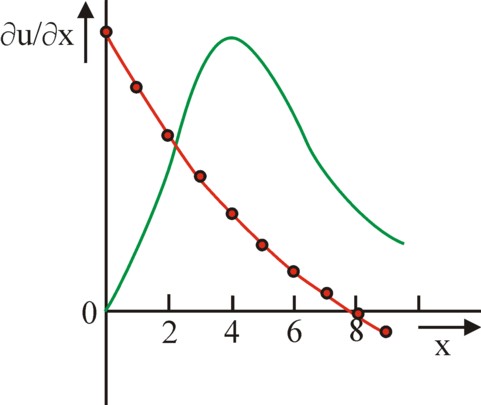
The law is presented in a graphical manner in the figure 1, for an arbitrary case. The black dots represent the added utility Δu, that the individual derives from the last acquired unit of product. The variable x on the horizontal axis measures the amount of product, which he possesses in total at that moment. The added utility Δu per unit of product is also called the marginal utility. When the addition is presented as a continuous process (red curve), then the marginal utility corresponds to the mathematical expression ∂u/∂x.

Note that the first law of Gossen uses a measurable utility. This is called cardinal utility. The individual is able to estimate that on average two units of the product provide less utility than one unit. Note furthermore, that the total utility can be calculated by means of a summation of all added utilities Δu(x) - or, what amounts to the same thing, to integrate the function ∂u/∂x. From the saturation point onwards an extra unit of the product is no longer useful. It becomes a burden, a displeasure, which is annoying.
Indeed the first law appeals to the common sense. Yet today other curves are used for the presentation of utility. The green curve in the figure 1 is the general shape of the marginal utility in the model of Bernard van Praag6. The curve suggests, that a very small quantity of the product is actually rather useless. Van Praag defends this behaviour by referring to the daily necessaries of life. It is impossible to survive on just one potato. A second difference of the green curve in comparison with the red curve of Gossen is observed for large quantities x. In the green curve of Van Praag the need for the product is never completely saturated. The (marginal) utility is never negative.
An alternative explanation of the shape of the green curve is, that in general the utility of a product is estimated as a part of a total package of products. In other words, the marginal utility of a product j is not ∂u(xj)/∂xj, but ∂u(x1, ... , xj, ... , xn)/∂xj. In practice some products tend to complement (supplement) each other. For instance, a light bulb is only useful, when electricity is available. Therefore the utility of a product depends on the living conditions and on the welfare of the concerned individual. The marginal utility ∂u/∂xj of the product j peaks there, where the quantity xj has the right proportions with respect to its other property.
Van Praag interprets his function of the marginal utility as a density function of a probability distribution. The he preference distribution of the individual can be used to estimate the average quantity μj of the product j, which he wants to own, as well as her variation σj². It is typical for density functions, that the surface beneath the green curve equals 1. In other words, the value of the total utility can never exceed 1. It is convenient to see the utility function as a distribution function, because thus use can be made of statistical laws.
The second law of Gossen expresses, that usually the individual wants to expend his budget or income on various products. The law states:
The total utility is maximal, when the added utility due to the expenditure of the last monetary unit on the product j equals precisely the added utility due to the expenditure on any other product k.
This law supposes, that the prices pj of all products are known, and constant. It is obvious, that here the utility function must depend on all quantities of products. She evaluates the vector x.
The second law can be formulated as a mathematical requirement for the maximal utility:
(1) ∂u/∂xj / pj = ∂u/∂xk / pk = λ
The parameter λ is a constant, which is called the marginal utility of the expenditure7. This expression is obvious. For xj×pj and xk×pk are the (perhaps marginal) money sums, which have been spent on respectively the products j and k.
The second law of Gossen allows to elaborate on the meaning of the marginal utility. For the sake of convenience the case is studied with just two products, numbered 1 and 2. Suppose that for a certain package of goods (x10, x20) the marginal utility of the expenditure on product 1 is larger than the marginal utility of the expenditure on 2. In that situation the utility is not optimal. Now in the common paradigm of the marginal utility the individual will decrease x20 somewhat in favour of x10. For the paradigm makes the hypothesis, that the marginal utility of a product rises strongly, according as less of it is available. Therefore the quantities x10 and x20can always be changed in such a manner, that finally the formula 1 is satisfied.
When the marginal utility assumes the shape according to Gossen (figure 1), then in the same situation with two products sometimes the requirement of the formula 1 can not be satisfied. An example can illustrate this. Suppose that the utility function is separable, and thus has the form u(x1, x2) = u1(x1) + u2(x2). Suppose that one has ∂u1(x1)/∂x1 = 3 − 0.5×x1 and ∂u2(x2)/∂x2 = 6 − 1.5×x2. So both marginal utilities fall in a linear manner, and not as a curve (such as in the figure 1). Furthermore let the prices be p1=1 and p2=3 (in units of money).
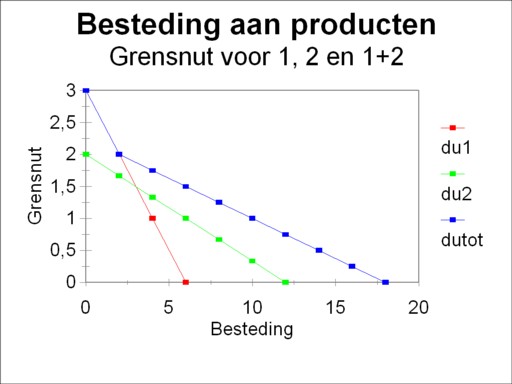
In this example the marginal utility of the expenditure on the product 1 is larger than the one for the product 2, as long as the total expenditure is less than 2 monetary units8. This individual will not buy a single unit of product 2, as long as his budget is below 2. In this budget range the product 2 is absent in his package of goods, as it were. As soon as his budget equals 2, the marginal utility of the expenditure has become equal to 2 for both products. At that moment the individual owns 2 units of product 1, and 0 of product 2.
Now when his budget continues to rise, the individual will acquire both products. And since the marginal utility of the expenditure on the product 1 falls 3× as fast as the one for the product 2, he will buy them in accordance with the ratio 1:3. His expenditures end at the moment, when he has 18 monetary units available for purchases. For at that moment the marginal utility of the expenditure becomes negative. In the mean time he has acquired 6 units of the product 1, and 4 units of the product 2. The figure 2 shows for both products their curves of the marginal utility of the expenditure, as well as the marginal utility of the total expenditure.
The loyal reader will undoubtedly recognize in this example the arguments, which Sam de Wolff has developed for his labour theory of value with two products. Indeed De Wolff obtains his theory of the marginal utility (lust intensity) directly from Gossen. In his book Het economisch getij he does not cite the later work of Jevons, Menger and von Böhm-Bawerk. Incidentally, your columnist is not familiar with the original publication of Gossen, and therefore can not separate the findings of Gossen and De Wolff himself.
In the present example the low budgets do not satisfy the requirement in the formula 1, because the marginal utility of the product 2 can not be raised sufficiently. Even for a quantity of 0 units of product 2 its marginal utility just equals 6. Apparently the shape of the marginal utility does matter. And the common shape, such as is presented in the introductory textbooks, is by no means self-evident9.
After the argument in the preceding paragraph the reader will perhaps not be surprised, that Van Praag proposes to value a package of goods with quantities (x1, x2) with a quantity of money equal to10
(2) y = C × x1α1 × x2α2
In the formula 2 C, α1 and α2 are constants. For the sake of convenience the argument is limited to two products, but it can be extended simply to the general case with n products. The logic of the formula 1 stems from the constants αj. They satisfy
(3) αj = ∂y/∂xj / (y/xj)
That is to say, when the quantity xj changes with a certain percentage, then the accessory budget y will change with a corresponding percentage. Here the parameter αj plays the role of the price elasticity. This implies that a changing monetary sum y will affect the quantities x1 and x2
(4) ln(y) = ln(C) + α1 × ln(x1) + α2 × ln(x2)
In a previous column about the work of Jacob van der Wijk it has been argued that the logarithm of a monetary sum can be interpreted as its utility. This seems logical, because people are inclined to judge large sums on the basis of Value-ratios and not on the absolute value-differences. Here this argument is applied to the quantities xj. Van Praag states also that ln(xj) is the relevant quantity, although he does not identify her with the utility. He weighs ln(xj) with the unknown utility distribution for every quantity xj of the product j, and integrates over all those xj values11. He calls this calculated value the centre of gravity of the utility distribution. In other words, the weighed average μj and the variance σj² of the quantity ln(xj) characterize the utility function of xj, in agreement with the preceding paragraphs.
Now when the so-called Central Limit Theorem is applied, which is well-known in statistics12, then one finds that the utility of the monetary sum y has a log-normal distribution with an average μy = Σj=12 αj × μj, and a variance σy² = Σj=12 αj² × σj². This is an interesting find, especially so since Van der Wijk has drawn the same conclusion! It is obvious that the present context is different. Van Praag employs the normal distribution of ln(y), and thus the log-normal distribution of y, for the utility, which the individual attaches to a monetary sum y, which is related to a package of goods x. The values of the average μy and the variance σy² are a direct consequence of the preferences of the individual with regard to the separate products in the package of goods.
In this way Van Praag applies the normal distribution to the marginal utilities of a given individual, which allows to calculate by means of integration the total utility of the variable y for that individual. The integration concerns y. On the other hand Van der Wijk applies the normal distribution to the fraction of individuals, which in the society dispose of a certain quantity of monetary utility. In this case the distribution function does not equal the utility itself. The integration concerns the utility. However, the cumulative utility distributions do have the same functional form in both theories!13
One of the most fascinating books, which your columnist has read in recent years, is Happiness quantified by Bernard van Praag and Ada Ferrer-i-Carbonell14. In the book many empirical studies of Van Praag and his colleagues during the past forty years are explained in detail. It concerns utility studies on many interesting policy areas, ranging from the income, health, housing, environment up to politics and the climate. Here the expression utility is applied in the sense of satisfaction and the experienced welfare. The authors even discuss the option to estimate the total well-being due to all those partial areas.
Perhaps it may come as a surprise, that Van Praag is able to measure satisfaction. For the problem of the individual utility is precisely, that it can not be observed. The utility is merely expressed in an indirect and veiled manner, through the effective demand of the individuals on the various markets. Therefore in almost all common introductory textbooks about economics it is stated, that theories must not be based on a cardinal utility. It would be best to limit the analysis to ordinal utility.
However in the preceding paragraphs it has been shown, that the cardinal utility is in fact indispensable for understanding the human behaviour and world. And people do have the feeling, that they try to estimate the utility by themselves in all kinds of situations. Now Van Praag has had the excellent idea to ask individuals simply and plainly about the utility, that they attach to all kinds of events! Incidentally, this idea is not truly brilliant, for questions about satisfaction are common in the research of related sciences such as the sociology and psychology. Only the economists appear to be shy of doing such a thing, or even averse.
In this paragraph merely some results of Van Praag with regard to the income will be discussed. The other themes will have to wait for future columns. The starting point of the empirical income studies is, that the incomes have a log-normal distribution with an average μ and a variance σ², such as has been assumed in the preceding paragraph. Van Praag uses mainly the data from the German socio-economic panel (GSOEP) survey of 1997. This collection contains the answers of almost 5000 German households on questionnaires. In particular he analyzes the answers of the households on two questions.
In the formula 5 g is the family size. The parameter ε is a statistical variable, which takes into account the individual preferences of the household. For the utility distribution of y is still different for each household. Van Praag finds for the probability distribution of ε a variance of 0.22. He does not elaborate on the units, which belong the the data of the GSOEP collection (undoubtedly DM).
The income evaluation question (IEQ): Given your personal situation, which monetary sum would you call a very low income? And a low income? An insufficient income? A satisfactory income? A good income? A very good income?
So the IEQ supplies 6 answers ηk for each household, which yields evidently more information than the FSQ. Van Praag assumes for these answers, that ln(ηk) (k=1, ..., 6) has a normal distribution N(μ, σ²). Thus it is possible to estimate the parameters μj and σj² of households j.
After analyzing all these IEQ answers in the GSOEP data Van Praag concludes, that a good description can be given with the model16
(6) μj = 0.527 × ln(yj) + 0.121 × ln(gj) + 3.61
He finds for the variance σj² a universal value of 0.21. In this empirical manner the log-normal distribution of the separate households has been determined! Who says that this is impossible? Van Praag calls this utility distribution the "short-term" welfare function of the household j. It is obvious that in this case the term with the family size gj is positive, because the respondents take it into account in their answers. For the answers of the IEQ are purely hypothetical.
According to the formula 5 the households are more satisfied, according as they have a higher income y. Yet here a caveat is justified. For in the formula 6 the average value μj of the welfare distribution for the household j turns out to depend on the own income yj. Apparently when the income of households rises, then the welfare distribution shifts to the right. In other words, when one obtains a higher income, then the preferences for an income are raised upwards. A higher income does not automatically mean, that the household is more satisfied than a household with a lower income. Van Praag calls this phenomenen the preference drift. The loyal reader may remember, that also Van der Wijk has introduced such a shift for the subsistence minimum in his model.
Unfortunately this drift of utility feelings attracts relatively little attention in the western economic literature, and that is certainly true for the introductory textbooks. The vision of the Leninist economist Val'tukh is clarifying in this respect, because she does acknowledge the central role of the dynamics in the utility function17. Val'tukh stresses in his book Entwicklungs-proportionen und Befriedigung der Bedürfnisse the historic origin of needs18. According to him the needs are the living conditions of the time, which are seen by the households as absolute necessities. The households make their demands on the basis of the living standard, which in their period is judged to be socially acceptable. In this regard they will in the first instance compare themselves with the group or class of the population, to which they belong.
An example may clarify this. Consider an individual from the lower social classes. He has merely a limited amount of needs, because the price of many products simply surpasses by far his income. The expensive product will not even appear in his utility function. When suddenly the wealth of this individual rises substantially, then he will still not desire those expensive products. It is more likely that he will try to saturate his already existing needs. But even this endeavour is difficult, because he has never reflected on this opportunity, and therefore is forced to adjust his preferences. A raise in welfare requires, that the preferences and utility functions are updated and developed further.
The time of learning, which is desribed here, pertains to the individual, but naturally also to his class as a whole (for instance: the emancipation of the working class), and to the society in her entirety. Val'tukh points out, that thus beneath the typical individual and subjective preferences a historical and socially determined progress is in full swing. When the science can predict these developments - and this is evidently possible to a certain extent -, then the economic growth can be directed and steered in a purposeful manner. For instance a glance at the famous pyramid of Maslow shows, that the higher mental needs will grow. The supply of services becomes an increasingly important part of the economy. This development occurs in time, but also in space, namely as soon as welfare spreads to the backward areas.
The satisfaction of the existing needs does not only approach her saturation point, but she also changes the structure of the needs. When new needs are formed (in the sense of a property or a quality aspect), then the old needs wil vanish. The utility function u(x) herself shows, that the needs are always connected. Val'tukh pleads for a certain amount of planning, so that at least the economic laws and tendencies are taken into account. A part of the needs has an objective character. In this manner the production structure can be adjusted to the changing structure of needs. The arbitrary personal deviations and peculiarities of the households, the subjective parts of the needs, can be studied by means of statistical methods.
Finally it must be noted, that the important explanation by Val'tukh is not utterly surprising. Val'tukh argues in the tradition of the German Historical School, which stresses the influence of the historical and cultural factors on the economy. This is translated analytically in the attempt to distinguish between successive social phases. In the method struggle between the Historical School, with as its main spokesman G. Schmoller, and the Austrian School, with K. Menger as its propagandist, the first has got the worst of it19. Especially in the modern western states the victory was so convincing, that the paradigm of the Historical School has sunk into oblivion. That is not justified. It is true that their approach has been continued in an adapted form by the Institutionalists (among others, Veblen and Galbraith). The idea of the successive historical phases has been adopted by the social-democratic ideology, which on that ground believes that the planning of the society is feasible. On the other hand, the liberals accept only one phase: the natural or liberal one.