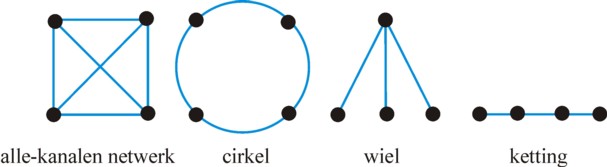
Figure 1: Several structures for a network of four
Group power plays an important role in economic systems. The present column presents three models of the abuse of power. First, the power distribution in networks is analyzed. It turns out that in bilateral exchange processes the power is determined by the position in the network. Next, the theory of rent seeking behaviour by interest groups is addressed. The goal is to redistribute the incomes. Finally, the theory of the tournament as a source of rewards is studied. The tournament can increase the motivation of risk-neutral workers, such as management.
Since its foundation, the Gazette has given a central place to power factors within the economy. Your columnist has always doubted, that human actions would be coordinated mainly by the invisible forces of the markets, such as is stated by the neoclassical paradigm in its traditional form. Social power is always exerted by and within groups. At the end of the nineteenth century, the marxist theory of power has made a lasting impression. However, it was always controversial, and nowadays is generally rejected1. Since the seventies of the last century the analysis of group power has become more popular, also among economists. The new findings are often presented under the name new institutional economics or new political economics.
The group uses her power in order to further het own material and immaterial interests. Power is used for exerting influence on others, in such a manner that they adapt their behaviour in the desired direction. For instance, power can be mobilized for spreading a certain religion among the people. The group mentally benefits from this, because each conversion is an affirmation of the personal identity. However, economic theories of power mainly place the material interests in the centre. Then the power aims to increase the welfare of the personal group. The present column describes several of the most popular theories of power.
The distribution of power naturally depends on the social relations between the various actors. The Dutch economist P. Frijters has proposed a taxonomy, which distinguishes between (loose) networks, reciprocal circles and hierarchies. This taxonomy is related to the categories, which have been proposed by institutionalists such as O. Williamson. At the micro level the bilateral or dyadic transactions between actors j and k in a network can be studied. An important approach is the so-called general Nask solution of the negotiation between j and k. The starting point is that thanks to the transaction the pair j and k can mutually share an income π2. Define xjk as the resulting income of j in this transaction with k. This is the reverse for xkj. The rational solution of the exchange is given by
(1) maxx(jk), x(kj) xjkbj × xkjbk
under the condition xjk + xkj = π
In the system 1 bj is the total bargaining power of j, and bk is the same for k. The solution of this problem is xjk = π × bj / (bj+bk), and evidently xkj = π − xjk. The value of bj depends on the type of the transaction. It is logical that bj will increase with the number of possible contacts nj of j with other actors, where also the total number of actors in the network is relevant (j, k ≤ n). Furthermore, the number of mutual connections or ties m in the network influences bj, because not all pairs of actors necessarily have a contact. In practice it turns out that it is convenient to combine n and m in the parameter w = (n+m) / (1 + n+m). The parameter w expresses, that in small networks j does not have much choice. And finally, the number aj of transactions of j is important, because during a time interval (period) j can conclude various transactions with his nj contacts3. Thus one has bj = bj(nj, w, aj).
In order to make bj more concrete, the position of each of the nj contacts in the network must be determined. This fills in the structure of the network. Suppose that the variable δjk indicates whether k has a contact with k, and in such a manner that δjk=1 represents a contact. Pairs without contacts, as well as δjj, are presented by the value 0 in the matrix Δ. This Δ can be used to derive the convenient matrix R, with elements ρjk = δjk / Σi=1n δik. Apparently, ρjk measures the importance of this contact for k in relation to all of his other contacts. Then the product ρjk×ρkj measures the combined weight of the contact for j and k together. When this product is large, then j can potentially control the pair relation. More generally, the network control of j is given by
(2) γj = Σk=1n ρjk × ρkj
For the sake of convenience, let Δ be symmetric, so that each contact is reciprocal. Then the network control of j obtains a simple form, namely γj = (Σk=1n ρjk) / nj 4. In other words, γj is the average of the importance of j for all other actors. Note that the actor j can determine his control γj without knowing the whole network. For a symmetrical Δ it suffices when he knows the importance ρjk of his own contacts. Thus one finally finds bj = bj(γj, w, aj), where nj is included in γj.

Usually networks with so-called negative ties are studied. A negative tie between a pair j and k exists, when k can close the same transaction with other actors i, when desired. In other words, k can replace (substitute) j by i. It is obvious, that k has more power thanks to the availability of alternatives such as i. In such a situation a large aj is unfavourable, because then j must spread his power over many transactions5. Now a conceivable form of bj is6
(3) bj = 1 / (aj × ln(1 / (w×γj)))
Since w×γj < 1 holds, the logarithm always is a positive number. This is even an important reason for the introduction of the parameter w. The formula originates from the mathematician and economist K.G. Binmore. The source of your columnist does not elaborate on this functional relation. It does remark, that the theory is applied often in laboratory experiments. Here it turns out that the formula gives a satisfactory empirical description.
It is perhaps clarifying to apply the preceding model to the four networks, which have been described in a previous column. For the sake of completeness, the four networks are presented again, in the figure 1. The networks all have n=4, but the number of contacts varies, namely respectively m=6, 4, 3 and 3. That is to say, in this order w is falling. Let Δ again be symmetrical, so that one has γj = (Σk=1n ρjk) / nj. The table 1 contains the matrices R for the four cases, as well as the network control γk. Besides bj is included in the table, under the assumption that aj=1. In each period each actor closes just one transaction. Due to the formula 2 the differences in γj are clearly increased in bj.
| all-channels network | circle | wheel | chain | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| j\k | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | |
| R | 1 | 0 | 1/3 | 1/3 | 1/3 | 0 | ½ | 0 | ½ | 0 | 1 | 1 | 1 | 0 | ½ | 0 | 0 |
| 2 | 1/3 | 0 | 1/3 | 1/3 | ½ | 0 | ½ | 0 | 1/3 | 0 | 0 | 0 | ½ | 0 | ½ | 0 | |
| 3 | 1/3 | 1/3 | 0 | 1/3 | 0 | ½ | 0 | ½ | 1/3 | 0 | 0 | 0 | 0 | ½ | 0 | ½ | |
| 4 | 1/3 | 1/3 | 1/3 | 0 | ½ | 0 | ½ | 0 | 1/3 | 0 | 0 | 0 | 0 | 0 | ½ | 0 | |
| γ | 1/3 | 1/3 | 1/3 | 1/3 | ½ | ½ | ½ | ½ | 1 | 1/3| 1/3 | 1/3 | ½ | ¾ | ¾ | ½ | | |
| b | 0.84 | 0.84 | 0.84 | 0.84 | 1.23 | 1.23 | 1.23 | 1.23 | 7.49 | 0.81 | 0.81 | 0.81 | 1.21 | 2.37 | 2.37 | 1.21 | |
In the all-channel network and in the circle the four actors have the same position, so that they all can exert an equal control. The consequence is that each pair of actors distributes the income π of their mutual transaction equally. Each gets π/2. This changes in the chain, because the actors 2 and 3 in the middle have more control than the actors 1 and 4 at both ends. In their transaction with 1 and 4, the actors 2 and 3 appropriate 66% of π. The wheel sketches a dramatic picture. The actor 1 is like a spider in its web, and can appropriate no less than 90& of π in his transactions with 2, 3 and 4. This is simply due to his favourable position in the network. For, although the figure 1 may suggest otherwise, the actor 1 does not have a social or hierarchical power. The functional equality of the actors follows from the assumption δjk=δkj.
Laboratory experiments have indeed shown, that the predicted distribution for the wheel in the figure 4 (so with n=4) agrees well with the empirical measurements7. However, for the chain a small but yet significant deviation is found. The chain is also studied for n=5, where the result does agree well. It turns out that the formula 3 gives good predictions for aj=2 and 3, at least for the chain (n=3) and the wheel (n=4). Yet another experiment has studied the wheel, where each spoke consisted of a chain of two actors (in addition to the actor 1 on the axis). According to the result, then the formule 3 overestimates the power of the central actor.
It is obvious that this model is amenable to criticism. It assumes, that all actors are about equally competent. In reality particular personal qualities can evidently lead to a better result. Furthermore, the model is not dynamic. Therefore it can not describe expanding networks8. A phenomenon such as power-distance reduction (MAR) is not considered, because the actors can not mobilize and expand their sources of power9. In spite of these defects your columnist is very impressed by the performance of the formula 3.
The absence of a hierarchical power is characteristic for experiments, because these commonly study reciprocal groups, where the test persons are brought together just once. Then rules, norms and rol patterns are absent. When a test person has a favourable position in the network (such as actor 1 in the wheel), then he simply represents a talented contact maker 10. For this reason the formula 3 is also probable for the behaviour on markets, at least in situations without dynamics and the like. Economic actors are often presented as mediators, who are inventive in designing new product. They are skilled in combining the production factors (labour, knowledge, capital, land)11. The best entrepreneurs structure their network in such a manner, that they maintain an optimal control. This gives them a competitive advantage over their competitors12.
Often the use of power in the economy takes on the form of rent seeking. Rent seeking is any behaviour, which aims to artificially increase the personal income. In other words, rent seeking leads a a transfer of income without any service in return. It is obvious that rent seeking does require an effort, for instance the lobby in favour of a certain political measure. But that effort does not add productive value, and therefore withdraws labour forces and means from the production. The effort undermines the welfare, and therefore is rejected by economists. A well-known example of rent seeking is the ambition of the enterprises to obtain a monopoly position. For, the enterprise can realize a rent (an extra profit), when it succeeds in eliminating the competition. Thus the income of the consumers is partly transferred to the enterprise, as a rent13.
The lobby will generally aim at politics and at the state bodies, because the administration of the state is responsible for the legislation. The administration has the formal power to grant concessions, to establish monopolies, and to protect the industries against competition. However, the industries are not the only seekers of rent. In principle any group can lobby for a rent, including workers, certain categories of households, politicians, and the public bodies themselves. This insight is fairly recent. At the start of the twentieth century, the state was still often depicted as a benevolent dictator, who by nature acts in the interest of the citizens14. This trust in the state interventions even was the basis for the ideology of socialism, and even more of Leninism. Their failure was perhaps a source of inspiration for theories of powera href="#L15">15.
Apparently the meaning of rent seeking is rather broad. For instance, even advertising is sometimes considered as a form of rent seeking16. In this view advertising is simply a lobby. The costs of the lobby can be a significant part of the rent. Sometimes several groups compete with each other for acquiring a rent, such as during the granting of a concession. The chance to gain the rent gives an incentive to make an effort, comparable to the first price in a tournament or lottery. It is even conceivable, that the groups together make more costs than the total rent brings in. Even the entrepreneurial profit could be interpreted as a rent, but that is not the habit. The normal entrepreneurial profit is generally interpreted as a reward for the productive effort of the entrepreneur.
The democracy is a political systen, which somewhat curbs rent seeking. For, the majority of the electorat demands that the political administration tries to further the general interest. As soon as politicians grant favours to particular groups of interest, or to themselves, then they run the risk of losing the following elections17. In the democracy there is always the option to organize a countervailing power, when the existing order is in danger of degenerating. The hurt citizens can unite in a pression- or interest-group. This view is propagated by the evolutionary institutionalism, which stresses the dynamics and innovation in the society. Nevertheless, the character of this dynamics is still energetically debated among economists.
The economist M. Olson has developed a group theory about the behaviour of interest groups18. An interest group engages in action in order to extort a rent from the state for her members. This creates a positive external effect, because all persons interested benefit from the rent, without exception. Therefore the persons interested are tempted not to engage in the action by themselves. This is called free riding (in the German language Trittbrettfahren). Their opportunism weakens the group power. It is known from sociology and from the social psychology, that small groups can have a strong cohesion, because the group members have a personal control over each other. One may consult the columns about economic networks and groups. Therefore they can limit the free riding within their group, and optimize their power.
On the other hand, in large groups there is anonymity, which makes them vulnerable to the problem of free riding. Therefore large groups are bad in organizing a countervailing power, as soon as a small group demands a rent for herself19. In principle the electorat is a countervailing power, but according to Olson it is informed poorly. He predicts that the state will become a plaything of the small interest groups. There is a growth of hurtful institutions, which petrifies the society and stifles innovation. It is remarkable that now Olson propagates, that the state acts as the supervisor of the interest groups. He presents the state as a benevolent dictator, and here ignores, that the state bodies themselves can be rent seekers.
The economist G.S. Becker has developed a model of power, which plays down the conclusions of Olson20. The model of Becker applies a micro-economic approach, where the outcome of individuals is studied. This is called methodological individualism. Suppose that there are two social groups, numbered 1 and 2. The group 1 lobbies for granting a subsidy σ to her members. This must be paid by the group 2, by means of a tax remittance τ. That is to say, one has σ = n×τ, where n is the relative size of the groups 1 and 2. Therefore the group 2 establishes her own interest organization, which lobbies against the measure. The effort of a lobby leads to a power γj, and costs cj, with j=1 or 2. Apparently one has γj=γj(cj), with evidently ∂γj/∂cj > 0. Moreover, the rent seeking reduces the social welfare by an amount of Δw = Δw(σ), with ∂Δw/∂σ > 0.
Suppose, that the lobby leads to a continuous change. So one does not have a tournament, with a winner and a loser21. Then the variable σ is a function of γ1 and γ2. Thus the outcomes for the members of the two lobby-organizations become
(4a) π1 = σ(γ1, γ2) − c1(γ1) − Δw(σ(γ1, γ2))
(4b) π2 = - (1/n) × σ(γ1, γ2) − c2(γ2) − Δw(σ(γ1, γ2))
Note that for both lobby-organizations πj depends on the lobby of the other party. The group j does not know the strategy of the opponent, and can not influence it. For, the lobby is aimed at the state. The optimization of πj requires ∂πj/∂γj = 0, where this equation must be formulated for each possible γk of the opponent. The result is
(5a) ∂σ/∂γ1 = ∂c1/∂γ1 + ∂Δw/∂γ1
(5b) ∂σ/∂γ2 = -n × ∂c2/∂γ2 − n × ∂Δw/∂γ2
The set 5a-b cab be used for calcultating the optima γo,1 and γo,2. For, the functions σ and Δw are known, and moreover each organization knows her own γj. The expressions γo,1(γ2) and γo,2(γ1) are called the best-reaction functions of respectively the organization 1 and 2. The reactions are called Cournot-Nash behaviour. The optimization implies that each lobby-organization can increase her power, until the increase of the outcome πj becomes less than the increase of the costs cj. Here the two organizations run up each other, because their power has an opposite effect on σ. In other words, one has ∂γ2/∂γ1 >0 and ∂γ1/∂γ2 >0. Finally this ends in an equilibrium γo,1(γo,2), namely the intersection of the two best-reaction curves.
A concrete example can clarify this22. Let σ = 10×γ1 − 5×γ2, and Δw = σ²/1000. That is to say, the welfare decreases in an exponential way, according as the subsidy (rent) increases, Therefore even the group 1 will not want to raise σ without limits. Moreover, Becker assumes, just like Olson, that the lobby for the subsidy is started by a relatively small group 1. The counter-movement 2 is larger, and therefore less cohesive. This has the consequence, that one has ∂γ1/∂c1 > ∂γ2/∂c2. Therefore assume that one has γ1 = √(c1) / 20, and γ2 = (c2)1/3 / 20. Letn=1, so that σ=τ. A calculation with the set 5a-b yields the best-reaction functions γo,1 = 1/3×γ2 + 100/3 and 3×γo,2² + γo,2 = 2×γ1 + 100. The intersection of these two curves is (35.8, 7.4). The figure 2 shows the two best-reaction curves.
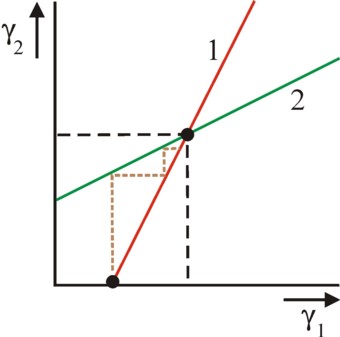
Apparently the lobby of the group 2 is useful. For, without the lobby of the group 2 (c2=0) the group 1 realizes a rent σ = 333 thanks to her effort with a size c1 = 55.6, and a profit π1 = 167. In this situation the group 2 makes a loss of π1 = -444. In the equilibrium the rent of the group q is merely σ = 321, despite the increased costs c1 = 64.1. The profit is decreased to π1 = 154. Now the group 2 must naturally make costs, namely c2 = 20.2. But thanks to the decrease of σ the group 2 yet keeps her loss constant at -444. For completeness, your columnist notes, that this example does illustrate the usefulness of the countervailing power, but also is constructed in a rather artificial manner23.
Becker interprets the result of his model in the following way. In society various interest groups compete with each other. The mutual competition prevents that a single group can enrich herself unjustly at the cost of the rest. Especially large groups will often defend the general interest, or at least take it into account. Moreover, the large groups can engage in transferring information to the voters. These groups use the public opinion to exert pressure on the politicians to reject unfair demands of small pressure organizations. This also curbs the welfare loss Δw. All in all, Becker is positive about the lobby organizations, because they also draw the attention to the existing injustices, and by means of their call for institutional innovation improve society. Note furthermore, that this positive judgement can not be derived from his formal model.
Furthermore, criticism on the view of Olson is warranted because of his neglect of neutral organizations24. Think about the scientific institutes, the independent media, and other independent inspectors. A wise state will educate its citizens well, so that they are capable of evaluating the lobby of the various interest groups. In such a society, lobby organizations give beneficial signals about the diversity of the existing needs. The loyal reader may remember, that according to the sociologists J.S. Coleman and R. Putnam the interest groups can even be identified as a social capital. Thanks to the social capital the economic transaction-costs are reduced.
Worth mentioning is the view of the mentioned Frijters on rent seeking25. His taxonomy makes an explicit distinction between small and large circles, precisely because of the difference in cohesion. He states that the class-theory can be interpreted as a theory of rent seeking, especially in the version of Olson. A striking hallmark is the emphasis on material interests. Frijters objects, that group processes are influenced by the cohesion and by the internal morals of the group. Besides, the theory of rent seeking pays little attention to the methods, that are used to exert power and influence. All in all, Frijters is positive about the lobby, and his views are congenial to those of Coleman and Putnam. By the way, note that Frijters is quite critical about the lobby of the banana industry in Australia.
Note that the theory of rent seeking is supported by the social psychology. People join a group or a circle in the expectation, that the membership yields material and psychological benefits26. The group has a common goal, and together gains power. The group reinforces the self-esteem. Furthermore, groups tend to polarize, which can result in the pursuit of high incomes. The members have a favourable opinion about their own group (ingroup favouritism, self-serving bias)27. The psychology states, that the competition for rare resources leads to conflicts between groups. This creates a hostile attitude, which is expressed in prejudices and discrimination. The group will become frustrated by the organized countervailing power. Therefore it is important, that institutions exist for solving the clashes between the groups in a peaceful manner28.
Your columnist can not refrain from speculating about the meaning of rent seeking for the trade union. For, she is an eminent example of the ambiguous character of the lobby. The trade union movement wants to redistribute the incomes. During the nineteenth century, the heydays of classical liberalism, the emerging trade union movement is the exponent of the justified needs, which live in the proletariat. According to marxism, the entrepreneurs appropriate an excessively large part of the produced surplus value. The socialist trade unions want to solve this radically by expropriating the property of the capitalists. The collective agreement monopolizes the formulation of the labour contract, but is nonetheless valued as a useful institution. The minimum wage and the protection against dismissal are legal forms of rent seeking, which are of old controversial.
During the sixties the trade union movement gains power thanks to the full employment. It demands high wages to such an extent, that the profitability of the industries is structurally affected. This is truly a weird period, because under the influence of the New Left the media and even parts of science give up their neutrality, certainly in the Netherlands. Perhaps Olson mainly refers to this spirit of the time in his model. Then the trade unions demand a (too) radical participation in management. The social trade union movement emerges, so that unions become quasi-political bodies. During this period the rent seeking had dogmatic and irrational traits. Nowadays the trade union movement struggles to prove its reason of existence - incidentally just like many other collective associations. Paid propagandists enter the enterprises as organizers.
The theory of the principal-agent shows, that workers can seek rent. This problem occurs for instance in shift work, where the labour productivities apj of the separate workers j can not be distinguished. That is to say, an individual reward, based on result, is not possible. Now the enterprise can decide to base the individual wage on a tournament-system29. Here the extra efforts ej are registered for each worker j, and that ej determines the individual wage. Since the effort does not have a direct relation with productivity, the wage height is rather arbitrary. In the tournament system the wage has the form of a "first price". Suppose that the workers are risk-neutral, such as in the case of managers, as far as they possess some personal capital. Their apj can actually not be measured, and the tournament appeals to their already competitive attitude.
The present model considers a tournament between two workers j=1 and 2. The standard wage is π, and the first price is a bonus or premium Δπ on top of that wage. Let ej be the truly supplied effort by j. It is accompanied by costs c(ej). Suppose that the enterprise can register ej only inaccurately, so that it measures a value ηj = ej + εj. The uncertainty εj in the registration is represented by the density function f(εj), which for the sake of convenience is assumed to be the uniform distribution (f=1), on the interval [-½, ½]. Let p(ej) be the probability, that j wins the premium Δπ with his effort. Thus the expected utility of j becomes
(6) Euj(ej, Δπ) = p(ej)×Δπ − c(ej)
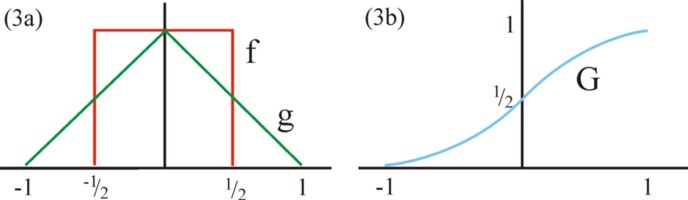
Suppose for the sake of convenience, that one has c(ej) = β×ej². The worker j maximizes his utility by means of Δπ × ∂p/∂ej = 2×β×ej. The theoretical challenge is to calculate ∂p/∂ej. The worker 1 wins the tournament, when η1>η2 holds. This is identical to e1 − e2 > ε1 − ε2 = Δε. Since Δε is at most 1, the winner is clear for the case |e1 − e2| > 1. When this does not hold, then a somewhat more complex argument is needed. Since the probability distributions f(εj) are known, the density function g(Δε) can also be determined with the help of statistical theory. It is an equilateral triangle on the interval [-1, 1], as is shown in the figure 3a 30. The corresponding cumulative distribution function G(Δε) is shown in the figure 3b. Note that the probability p satisfies p(η1>η2) = p(Δε < e1 − e2) = G(e1 − e2). Therefore one has ∂p/∂ej = g(e1 − e2). So in the optimization of Eu1(e1, Δπ) the two "legs" of the triangle in the figure 3 b must be distinguished
(6a) eo,1 = (1 − (eo,1 − e2)) × Δπ / (2×β) for eo,1 > e2
(6b) eo,1 = (1 + eo,1 − e2) × Δπ / (2×β) for eo,1 < e2
These are the situations of uncertainty, which lie in the area |e1 − e2| ≤ 1. The figure 3b shows, that the worker can increase his probability p by making a larger effort. He wil optimize Eu1 by equating eo,1 to (1 + e2) / (1 + 2×β/Δπ) and (1 − e2) / (-1 + 2×β/Δπ) for respectively the cases 6a and 6b. This is the best-reaction function for worker 1, and the one for worker 2 is naturally similar. See the figure 4. Suppose that initially ej=0 for both workers. The competition between the two workers mutually motivates them to outdo each others effort, in conformity with their best reaction, until this no longer pays. Again there is a Cournot equilibrium, which is located in the intersection of both best-reaction curves. In the equilibrium one has eo,1 = eo,2 = Δπ / (2×β), so that thanks to the tournament a total extra effort of Δπ/β is made.
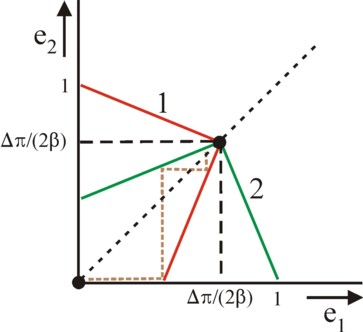
The tournament could be called a rat race31. The tournament stimulates both workers to make an extra effort. Since they end in the equilibrium eo,1 = eo,2, it would have been better to remain in the point (0, 0). However, this point is unstable, because the workers do not know each other's reactions. One could complain, that the tournament raises the work load. And the material incentive can lead to the suffocation of the intrinsic motivation (crowding out). On the other hand, the extra effort has a positive effect on the welfare. And this is beneficial for everybody. The culture of the enterprise must be such, that the personnel can act decently in the tournament32. For, the tournament is actually a struggle for power, where it pays to belittle and slander the effort of the other. The cooperation can become impossible, when cohesive group morals are not stimulated at the same time.
So it does not surprise, that the social psychology is ambiguous about competition between group members. The psychology acknowledges that incentives are needed in order to stimulate the workers to make an effort33. But they cause various side effects. Competition can seduce the workers into stretching their competences34. This can even lead to conflicts about group targets35. Prejudices and hostility can emerge within the group. The participants in the tournament can each form their own coalition within the enterprise36. This conflicts with the idea behind the enterprise, which is precisely established in order to further cooperation.
The formation of coalitions can be a conscious choice of the enterprise, such that it includes self-steering teams within its organization structure. In the former Leninist states the economy was permeated with a "socialist" idea of competition37. Then the competition is seen as a hallmark of the healthy personality, provided that it is embedded within humanist relations. The enterprises are encouraged to exceed the planned task. Working groups (collectives, brigades) are formed in the workshop38. The individual wage is supplemented with premiums and collective rewards, which are coupled to the performance of the working group39. The premiums are roughly 10% of the wage. Although the premiums are primarily coupled to productivity, they are also paid for innovations (Neuerer-Bewegung). The premiums are also meant to incite the weak groups (tournament effect).