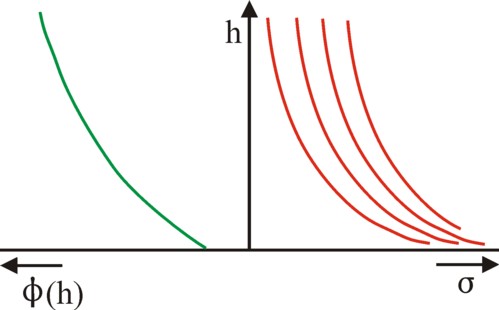
Figure 1: Left: utility functions (tilted)
Right: quasi-linear indifference curves
A large part of the twentieth century the economic debate was dominated by the controversy between the adherents of the liberal and planned economy. The question is how far the state should go in providing for the human needs and group interests. The present column first describes the view of the Leninist economicst Belousov (with thanks to the second-hand bookshop Helle Panke in Berlin). Next it is explained how the liberal theory of the Walrassian equilibrium models the supply of public goods in a Pareto optimal situation. This column builds on previous columns about the social utility function and about the marginal utility of money.
The theory of neoclassical micro-economics is built on the paradigm of the Austrian School, which considers a system of isolated households and firms. Although this paradigm yields many interesting insights, yet its description of reality is dissatisfactory. This column wants to draw the attention to the importance of the cohesion between all interest groups, that are active in society. This perspective is perhaps most cleary elaborated by the scientists in the former Leninist states in Eastern Europe. Besides, the more philosophical and sociological analysis of needs is scarce in the capitalist specialized literature. Therefore it is worth studying the Leninist views. An interesting one is given by the economist R.A. Belousov in his book Plan, Interessen und Äktivität der Werktätigen (an acquisition which originates from the second-hand bookshop Helle Panke in Berlin)1.
Belousov makes an interesting distinction between the needs and the interests. The needs are felt by the individual as something, that is wanting. The interests are a special form of needs:
Often the satisfaction of needs is not absolutely necessary for survival. She exceeds the material means for the physical well-being, and includes all kinds of intellectual achievements, which further the individual growth. The human development occurs within the society, and therefore it is a social process2. Thus many needs are transformed into group interests. The demand is collective, and this has consequences for the organization of the supply. A significant part of the satisfaction of needs must be executed without the use the markets, by means of public facilities. In the social perception the preference for a certain ideology develops. This can also be called a reason or rationality.
According to Belousov the needs have a hierarchical order. The needs of the community get the highest priority. Incidentally those needs coincide completely with the human well-being. They are summarized in the fundamental socialist law:
the ultimate policy target is the growing satisfaction of the increasing material and cultural needs of the people, by means of a continuous development and improvement of the social production.
This illustrates how the demand resulting from the needs, is confronted directly with the possibilities in the productive supply. It shows, that the needs and interests are the engine of the economic growth. The community can realize good socio-economic boundary conditions, but she can naturally never satisfy all personal needs.
The needs of the various collectives (enterprises, state organizations, social institutions) are subordinate to those of the community. In short, the state and its organizations introduce a certain order in the needs. Therefore the satisfaction of subordinate interests is bounded. The lowest level is formed by the satisfaction of individual needs. The hierarchy is reflected in the structure of the policy plan, which contains the instructions for the management.
The hierarchical ordering of needs is unavoidable. Some individual needs are harmful, and must be discouraged. That varies from the worn-out example of the smoking of tobacco, to dissolute behaviour and crime. In such cases it is the duty of the state and its organizations to point out the right direction. They have the legitimacy to weigh the various economic, political and ideological factors. The execution of the policy requires first of all, that the society is ordered by means of laws, rules and institutions. In addition the state influences behaviour by means of propaganda, advertising and guidance. The people must remember the consequences of their ideology. Often a soft approach suffices, because many individual needs are elastic and allow for substitution.
In addition to these instruments the state can efficiently influence the needs by the application of economic incitations. In this case the state uses the market mechanisms in order to execute its policy. Needs are addressed in order to realize other needs. Consider for instance the price policy, including the price of labour. The minimum wage incites the enterprises to raise the level of productivity. And wage incitations create some competition among workers and workers collectives. The height of the product prices determines the profitability of the enterprises. Etcetera.
Belousov points out that in the modern society many needs are mutually connected, A large material welfare can only be achieved, when certain needs are satisfied, with regard to knowledge, health, security, and challenging labour3. In other words, sometimes there can be a conflict of needs. Consider for instance the limitation of work stress, which will also slow down the productivity. In particular unemployment can be an effective instrument for raising the labour intensity. Here the society must set her own priorities.
The ideology is present in all aspects of human life. It is undeniable that she affects the economy. For instance: on the one hand the individuals prefer a diverse assortment of products, which allows them to choose in accordance with their preferences. Moreover, the differentiation of products provides a means to the producer to distinguish himself, and thus obtain a monopoly position. On the other hand the economic efficiency requires, that products are standardized. This is desirable in order to further substitution and maintenance, and to increase the scale of production. The dividing line between a versatile development and a short-sighted vanity is only possible on ideological grounds4.
Next to the sifting out of contra-productive needs the plan must also indicate the order of the future satisfaction of the legitimate needs and interest. For it has just been stated, that the availability of resources puts a limit on the production. According to Belousov the plan reconciles the conflicts of interest, because it is justified by scientific arguments, and is laid down in a democratic manner5. Yet on this point his arguments are somewhat poor.
For instance, in his discussion of the income distribution Belousov merely remarks, that everybody receives according to their labour performance. But there is no scientific measure for the utility, that is derived from an income by the various groups and collectives. The wage scales are determined simply in an administrative procedure. It is obvious that the planning agencies will favour certain groups within the population, which are beneficial for the political system, notably the leading elite in the army, the politics, the economy, the art and science. It is unclear why that process would lead to a just weighing of interests. This problem is especially annoying, since the Leninist centralism does not allow for ideological competition.
In the eighteenth century the economist Adam Smith developed the idea, that the economy by itself, guided by an "invisible hand" as it were, moves towards the optimal state of equilibrium6. In the nineteenth century the economist Léon Walras built on that idea his mathematical equilibrium model. The Austrian School (Carl Menger) and Stanley Jevons supplemented this model with theories about the ratio of exchange. In the beginning the model addressed indeed the barter economy, but later it was extended with a productive sphere. Now the equilibrium is called competitive, because it is assumed that the producers optimize their profits.
Finally, Vilfredo Pareto, the successor of Walras, proved that in the general Walrassian equilibrium the available means are used in an optimal manner. Within the reigning system of proprietary rights all resources are wisely allocated. The households (consumers, numbered as i=1, ..., N) optimize their individual utility ui, and the separate producers (as representants of the products, numbered as j=1, ..., M) optimize their profit πj. The resulting state is called Pareto optimal or Pareto efficient. An economic state is Pareto optimal, when no other alternative leads to a higher individual utility for some without diminishing the utility of others. Your columnist hopes to elaborate on this paradigm in a future column. That is no simple task. In short, as a provisional refresher for the initiated reader: in the general Walrassian market equilibrium the households and the producers are both price takers. The realization of Pareto efficiency is based on three pillars:
It is often overlooked, that in the context of the neoclassical paradigm the concept of optimality refers merely to a complete utilization of all possibilities within the reigning order. The starting point of the equilibrium model is an already existing distribution of wealth, and she can be very unjust. Even when very skewed property relations would in a compelling manner excite the social revolution, then still the ancien régime could be Pareto optimal. On the other hand, the state can change the property relations in a quiet manner (for instance by democratic means), and next realize the Pareto optimal situation7.
So the neoclassical paradigm can not indicate, when the optimum of the social welfare has been reachted. The reason of this deficit is, that the paradigm considers merely the satisfaction of an individual. It is not necessary and perhaps impossible (and this view has been stated first by Pareto) to attach a value to the utility (cardinal utility measurement). Only the order can be determined (ordinal measurement). Moreover, the strong statement is made that the utilities of two individuals can not be compared. A sandwich during a plentiful dinner can yield as much utility as (or more than) a sandwich for a hungry homeless person. A consequence of Pareto's statement is, that no social "cardinal" utility function would exist.
Yet it must be admitted that Pareto optimality in itself is a desirable state, An essential aspect of the view of Pareto and the Austrian School is, that the economy is determined completely by the isolated households and enterprises. The utility function of a household has the form ui(x1, ... , xM), in vector notation ui(x), and thus other households are totally absent in it. This approach stands in a stark contrast to the previous analysis by Belousov. It is clear that the paradigm of Pareto is a rigorous abstraction. Therefore the western economists have later tried to integrate collective effects in it.
Now the question is how in the fundamental model, where all economic actors act in a social vacuum, the social interactions can obtain their deserved place. It is strange that the Leninist economists have hardly paid attention to this scientific challenge, in spite of their excellent evaluation of the theoretical deficits8. All findings in the following paragraphs originate from western studies. They search for the individual utility function ui(x, h) of the household i, where h expresses the influence of the society as a collective. When h represents the interaction with another private actor, then she is called an externality. However, following Belousov this column focuses the attention on the influence of those public goods, which are produced and supplied by the state9. The market externalities are ignored and kept as a theme for a future column.
A public good has the special property, that it is available for all households. When one households disposes of the public good, then the other households have automatically tha same pleasure. Nobody can be excluded from its use. Once the public good has been supplied, than its use is inexhaustible. An example is infrastructure such as parks, monuments, roads and bridges. Security is another, for instance dikes, lighthouses, and the army. Culture and recreation are ofteh also a public good, for instance generally available knowledge and information, electromagnetic waves of radio and television broadcasting, or public nature reserves. In the planned economy even the enterprises are a public good, albeit with many restrictions. It is obvious that here the question is, who will pay for these goods, now that the individual appropriation is not necessary. It is tempting to be a free rider. This aspect is discussed in the following paragraph.
The description of such a complex economic system requires complicated mathematical methods and techniques. For didactical reasons it is common to make simplifying assumptions. One is the assumption of the partial equilibrium, a find of Alfred Marshall. That is to say, the model considers merely the trade in a single market, while all other markets remain unchanged. Thanks to the columns about the neoricardian model the loyal reader knows that this assumption is wrong. However, one may hope, that the corresponding error can be neglected. Then the prices on the other markets remain constant. For the sake of convenience they can even be aggregated, and represented by a composite product with quantity σ and price ps.
Thus the utility function contains two products: the public good with a quantity h and a price pg(h), and in addition the composite market product. The public good is sold on the partial market, with the state as its only producer and supplier. The state is a monopolist, and can dictate the price. States do not make profits, but they minimize their costs c(h). Therefore the price is given by pg(h) = c(h)/h 10. Suppose that the cost function c(h) is convex. In other words, she increases progressively with the quantity h. This is expressed in the formulas ∂c/∂h >0 and ∂²c/∂h² > 0.

Next it is assumed that the indidivual utility function of the household i can be separated in these two products. Thus the utility function gets the form ui = ψi(σi) + φi(h). This can be simplified further by chosing ψi(σi) = σi. Now the resulting utility function of the household i is11
(3) ui = σi + φi(h)
The functional relation in the formula 3 is called quasi-linear. The explicit choice for this function means, that the remainder of the present discussion uses cardinality! There are several additional requirements for the derivatives of φ, namely ∂φi/∂h >0 and ∂²φi/∂h² < 0. These requirements simply imply, that φi has a concave shape, as is illustrated graphically in the left-hand part of the figure 1. It is clearly visible, that the marginal utility ∂ui/∂h = ∂φi/∂h of the public good (the slope of the curve) is falling. In the right-hand side of the figure 1 several indifference curves (iso-utility curves, where the utility is a constant) are drawn in the (σi, h) plane. They have all similar shapes, apart from the shift along the σi axis.
At the start of the column it has been stated, that the households maximize their individual utility. Therefore in the partial market of the public good one finds the formula
(4a) max (σi + φi(h)) voor σi≥0 en h≥0
(4b) onder de voorwaarde dat ps×σi + τi×c(h) = wi
In the formula 4b τi is the fraction of the costs for the public good, which the household i remits to the state. The variable wi is the income of the household. It is commonly supposed that the household spends his entire income, so that the formula 4b is an equality and not the inequality ≤.
In the paragraph about Pareto optimality it has been discussed how for a product on the private market the marginal utility of the product, the product price, and the marginal utility of money λ are connected. In the formula 4a the assumption of the partial market implies, that the quantity of composite product σi is much larger than the utility of the single public good φi(h). Now it follows for the composite good that one has λ = 1/ps. For this reason the composite good is called the numéraire.
Now insertion of σi from the formula 4b in 4a leads to the requirement
(5) max (φi(h) − τi × c(h) / ps) voor h≥0
For the term wi/ps does not depend on h, and is therefore irrelevant for the maximization. The sum in the formula 5 results, under the assumption of a payment of Σ1=1N τi = 1 which covers the expenses, in
(6) max ((Σi=1N φi(h)) − c(h) / ps) voor h≥0
Therefore the Pareto optimal solution ho of formula 6 must satisfy
(7) Σi=1N ∂φi/∂h(ho) = ∂c/∂h(ho) / ps
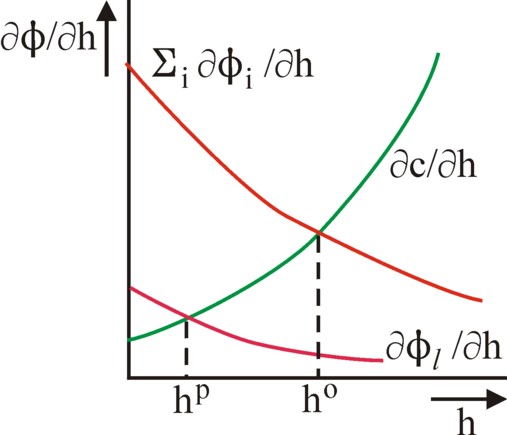
The formula 7 is the condition of optimality for public goods, which has been discovered by the famous economist Paul Samuelson. The sum of the marginal utilities of the public good for all households must equal the marginal costs for the production of the public good.
This identity can always be satisfied, because φi is concave and c is convex. The curves of the aggregated marginal utility and of the marginal costs are shown graphically in the figure 2. It is clear that the optimal supply ho is determined by the intersection of both curves. The figure 2 has a striking resemblance with the familiar demand- and supply-curves in the quantity-price picture. However, in such pictures the curve of the aggregated demand are constructed by a horizontal superposition of the separate demands of the households. For the households are price takers. On the other hand, in the figure 2 the summation for the aggregated utility implies, that there is a vertical superposition. Here the households are quantity takers.
It is desirable that each household i consumes its needed quantity hi of the public good in agreement with the formula 5. However, this urge will be minimal, when other households j<>i have already paid a certain amount of the public good. In principle i is willing to pay, but evidently not in a situation, where others already supply the goods for free. In that case the supply of the public good will exactly equal the amount, that its biggest lover (say household l) is willing to consume. To be precise, when a private enterprise (without the power to enforce payment) supplies the public good, then the quantityhp can be calculated from the condition
(8) ∂φl/∂h(hp) = ∂c/∂h(hp) / ps
In the figure 2 it is shown graphically, how the value hp is derived from the marginal utility of the household l, which is obviously smaller than the aggregated marginal utility. The sought value is found at the intersection of the marginal utility curve and the marginal costs curve. Those households, that are most willing, will finally pay for the quantity hp of the public good. In any case the household l as its biggest lover is obliged to pay in order to fill up the quantity until his own preferred level is reached. The others, who have not paid anything, enjoy the supply hp as free riders.
Yet it can not be concluded, that in this situation with a private supplier the needs are satisfied in an optimal way. The equilibrium is not Pareto optimal. For that requires a quantity ho. In the given situation there is apparently an insufficient amount of the public good. Some households, who are completely willing to pay for the public good, have evaded this obligation12. So an actor is needed with a coercive authority, in case the state, who squares the accounts with all households for the quantity of the public good, thta the truly want to have.
The state disposes of many tax instruments for collecting the money for the public good13. First of all he will ask the question what amount of the public good he will supply. When opinion polls are held among the households in order to determine the shape of their φi(h), then subsequently the state can calculate ho from the formula 7. Next a decision must be made with regard to the costs that each household must bear. In other words, the variables τi must be determined. There are three common tax principles:
The second and third principle clearly do not lead to an optimal equillbrium for the various households, because they do not pay in agreement with their needs. Then the quantity ho loses her self-evident nature. In this situation the quantity h of the public good could be determined well by organising for instance a referendum, an inquiry or an opinion poll. Then the analysis has a resemblance with the game theory, which studies how citizens manipulate polls and votes. Indeed for instance the election polls give reason to suspect, that people sometimes give dishonest answers. For your columnist the problems of such strategic voting behaviour are somewhat too cynical, at least for the moment.
The preceding argument makes clear, that the neoclassical paradigm of public goods contains useful elements for planned economies. The planning agency can naturally never determine the τi of all separate households. But it must be possible to divide the population in categories (workers, officials, rentiers, the aged, etcetera) with an approximately equal τivalue. Polls and measurements can be employed in order to determine the consumer normatives of such a category14. When these are combined with the formula 7, then also the optimal volume ho is known. And this is indeed exactly the method, which has been generally applied by the former Leninist states in Eastern Europe. It is satisfying to discover here the theoretical justification.