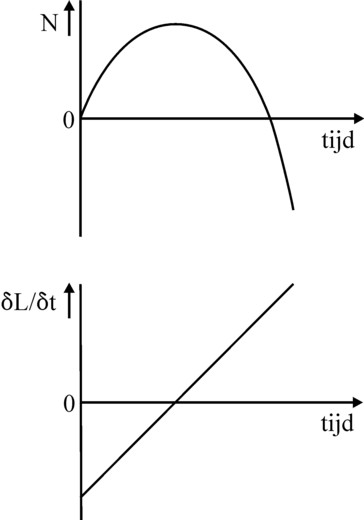
Figure 1: Utility N and marginal
disutility ∂L/∂t
Following H.H. Gossen and W.S. Jevons Sam de Wolff bases his theory of value on the disutility of labour. In this way he opposes the Austrian School, that denied the existence of a relation between the production costs and the value of the end products. In the Austrian view the value originates completely from the subjective preferences in the consumption. In the course of time this standpoint has become common in the economic science, albeit with some nuances. It is worth while to once more compare both standpoints, because in all his controversies De Wolff has always exhibited a sound intuitive sense.
The idea, that besides pleasure (utility) also pain (disutility) determines the human preferences, has been formulated ages ago. Jeremy Bentham (who lived from 1748 until 1842, and incidentally was a rather unsociable scientist) developed a philosophy that is founded on the largest happiness principle. Pain is bad. In 1854 this idea was picked up by Hermann H. Gossen, who has expanded her into an economic theory of the marginal utility. Unfortunately the spirit of the time was not yet ripe for the proper appreciation of the work of Gossen. More than fifteen years later, in 1871, both William S. Jevons and Carl Manger rediscover independently of each other again this concept. Now it does catch on. Incidentally only Jevons introduces the concept of disutility in his argument, and not Menger.
Sam de Wolff calls himself a marxist, so that he ought to reject the neoclassical value theory, that is based on the human subjectivity. Value is produced during the production, as an objective asset. Yet he has to a large extend shared in the euphoria about the marginalist analysis, which in his era had come on firm ground. His marxist position becomes apparent mainly in his persistent resistance against the Austrian School, which then had important supporters like C. Menger, E. von Böhm-Bawerk, and F. von Hayek. In his main economic work Het Economisch Getij De Wolff invokes the publications of Gossen and Jevons for his counter-attack, and he seems to cite in particular the text of Gossen (without clear references)1.

De Wolff could not resist the temptation to invent new names for the analytic concepts in the theory. Where Gossen writes about pleasure in life (Lebensgenuss)2 and Jevons about utility3, there De Wolff chooses the name lust. And where Gossen and Jevons use the word inconvenience (Beschwerde respectively disutility), and others use the word Leid, there De Wolff prefers the name onlust. But for the rest De Wolff seems to apply simply the examples of Gossen. See an earlier column about this theme, as well as its elaboration. In imitation of Gossen he even models the marginal lust and onlust (called intensities by De Wolff) by means of linear functions4.
Both Gossen, Jevons, and later also Alfred Marshall start from the hypothesis, that under favourable conditions the work can be a pleasant and spiritually enriching activity. Labour becomes an onlust only, when the working-day is too long, or too intense, or when the conditions are otherwise inhumane. The figure 1 shows the utility of labour (casu quo disutility) N = −L and the marginal disutility ∂L/∂t as a function of time, like Gossen imagined5. In the picture below the marginal utility changes into a disutility, as soon as the horizontal axis is crossed. From that point onwards the labour obtains a special meaning, because the phenomenon of the disutility has the consequence, that the people put a clear limit on the number of hours, that the are prepared to work.
In the columns just mentioned a Robinsonade (originating from Gossen) is used to show, that the worker determines his working hours on the basis of the amount of goods, which he can produce during that time. Those goods yield a certain pleasure, and by doing so compensate for the onlust of the labour. The consequence of this model is, that the value of the goods is related to the expended number of working hourse. The production costs determine (partly) the value of a product unit.
This is worth a moment of reflection: a worker does not stop working, because he prefers to do a more pleasant activity. His motive is not the temptation of leisure time. No, it is the subjective aversion against additional working hours, which incites him to stop. The German sociologist Frank Deppe states:6 "In general workers experience their labour as a heavy load, which is insignificant in content, and which is seen and perceived as a means for survival (one does not live to work, but one works to live!). The work itself is without any interest, and causes merely resignation". Apparently the quality is miserable. Incidentally also the reader may recognize this feeling, and sociological studies are not needed to obtain this insight.
Thus the onlust intensity of labour seems to be an excellent concept for studying the wage and the supply of labour. Your columnist has searched the world wide web, but without results. In particular one wonders about the role of the labour productivity (ap) in this argument. The behaviour in the figure 1 is derived for a constant ap. However, if the worker is not free to stop working, then he will undoubtedly resort to decreasing his ap. The future onlust can be controlled. But admittedly your columnist does not know an economic theory, which models this phenomenon.
The representatives of the Austrian School have vehemently attacked the idea of the disutility. According to Spencer especially Von Böhm-Bawerk and Von Hayek wanted to discredit the labour theory of value of Karl Marx, and therefore they refused to attach meaning to the production costs7. In the Austrian paradigm all product value is caused by the subjective needs and preferences of the consumers. In their view the quality of labour is unimportant. This eliminates the debate about the exploitation and alienation of labour, which is leading in the political economy of Marx.
In the Austrian perspective the consumption determines all values, and that pertains even to labour. For the worker chooses the number of working-hours according to his need for leisure time. On the one hand his total wage rises, when he works longer. Then he can buy more consumer products, and these yield an additional utility. The opportunity costs, that he must pay for the extra work, consist of the renouncement of the leisure time. In this way he again gives up some utility. The worker himself chooses the length of his working-day, in accordance with his consumptive preferences.
The new paradigm, which later was named the neoclassical theory, is a rupture with the past, when the classical theory still dominated. In the classical theory the product value is derived from the production costs, including the expenses for wages. In the new paradigm the wage costs are completely absent, with regard to the price formation of the commodities. All prices are formed in the exchange process on the basis of subjective needs, and they are related to the scarcity of the products. Then the wage costs are merely relevant for the supply on the labour market. The labour is simply a means for the worker in order to obtain an income, which satisfies his need for consumer goods. The disutility of labour as a determining factor is eliminated. Time is a scarce commodity. That pertains both to the labour time and the leisure time. Leisure time is presented as a good, which is instrinsically pleasant8.
Now the reader will understand, that according to your columnist the Austrian paradigm is an impoverishment with respect to the paradigm of Gossen, Jevons, and De Wolff. The element of labour is missing, the disutility (inconvenience), which in practice is so obvious. Of course the Austrian position can be attacked with intellectual arguments. For instance Alfred Marshall stated, that many unemployed workers endure their leisure time as if it is an inconvenience instead of a pleasure (utility). That is true, just like labour can sometimes be a pleasure. The fundamental criticism is evidently, that the Austrian paradigm makes an unrealistic assumption in order to determine the size of the supply on the labour market.
The question naturally rises: why has the Austrian paradigm after all become the common opinion in the modern economy? In the end Spencer identifies two reasons9:
Your columnist does not warm to the Austrian and neoclassical model of the labour market. However, it is useful to describe it, because this is seldom done properly in the introductory text books. The present description originates from the excellent text book Volkswirtschaftslehre by M. Heine and H. Herr11. It is remarkable, that the disutility (in the interpretation of this model) is equated simply to the relinquished pleasure of leisure time.
The model is founded on a number of assumptions. There is one type of labour, so that the diversity of professional qualifications is ignored. And the working-time can be divided at will, so that a labour contract can enforce any number of working-hours. The market is perfect. In other words, monopolies such as the organizations of employers and workers, are ignored. Another crucial assumption is that the system is a so-called one-good economy. The capital and the wage exist of a quantity of a single product, which is commonly chosen to be corn.
It has already been explained in the preceding paragraphs, that the households (the worker) has to solve an optimization problem in order to maximize his utility. This problem requires a simultaneous decision:
Thus the utility function of the households takes on the form
(1) N = N(tv, w)
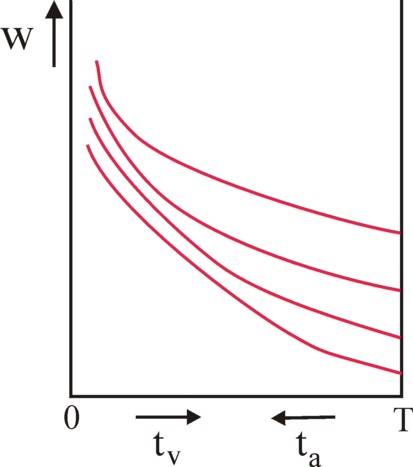
The utility function can be used to draw the indifference curves, which represent combinations (tv, w) with a constant utility value. The figure 2 displays four of those curves. The curves are valid for a limited time interval T, so that the range of tv values is bounded at the high end. The night's rest, meal-times, etcetera are excluded on the time scale, bacause these are not available as time. Then by definition the working-time is given by ta = T − tv. The coordinate axes of ta and tv have opposite directions. The slope of the indifference curves is given by
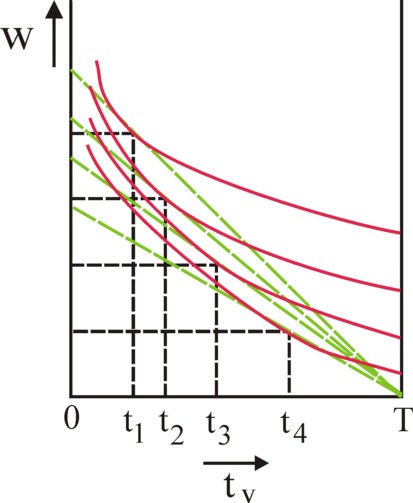
Figure 3: Budgets in the utility field
(2) dw/dtv = −(∂N/∂tv) / (∂N/∂w)
As is usual in this kind of analysis a budget restriction can be formulated:
(3) w = ωu × (T − tv)
In the formula 3 ωu represents the hourly wage, the wage level, expressed in a quantity of corn. Of course the term T − tv is simply ta. It is immediately apparent that the maximal possible wage wmax equals w(tv=0). The slope of the budget line is given by the wage level ωu. In the figure 3 the budget line is drawn for four values of the wage level.
It is known from the theory of the marginal utility, that the optimum of the household can be found by searching for the iso-utility curve, which just touches the budget line. The figure 3 shows these optima for the four displayed budget lines. Obviously the slopes of the iso-utility curve and of the budget line in the optimum are exactly equal. Then the formulas 2 and 3 lead to the relation13
(4) (∂N/∂tv) / ωu = ∂N/∂w
Finally the figure 3 allows to construct the supply curve A = A(ωu, N, T) of labour for the separate households. Then the optima of the households must be simply drawn in the cross of axes (ta, ωu). This is done in the figure 4. The social supply curve for labour from all households is obtained by adding for each value ωu the working-hours ta of all the separate households (workers). Then a curve is naturally found with a shape that is similar to the figure 4.
Your columnist has already complained about the absence of the disutility of labour in this argument. Moreover the explanation by Heine and Herr shows that the model is merely valid under certain limiting conditions. They draw attention to four points:
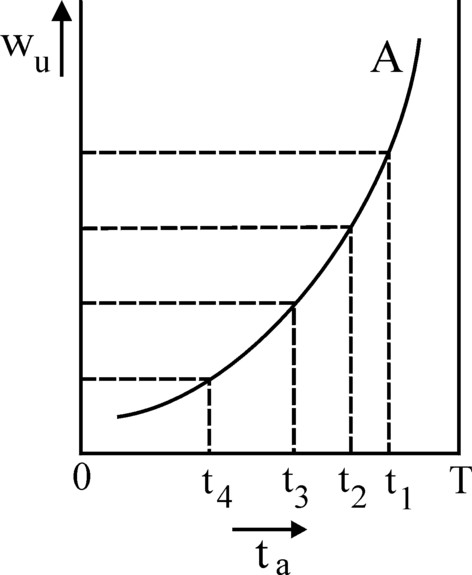
Figure 4: Supply ta = A(ωu, N, T)
The reader sees how Heine and Herr have a crushing criticism with regard to the neoclassical model of the labour market. This criticism almost pales the phenomenon of the disutility, which in principe is reconcilable with the neoclassical paradigm. It is naturally important to include in the neoclassical theory also the real costs of the production. But if Sam de Wolff would have known all this, he would perhaps indeed have omitted several chapters in Het economisch getij.
In several columns it is explained how Sam de Wolff uses a so-called Robinsonade in order to relate the lust intensity LIn of a product n and the onlust intensity OI of the labour. For the sake of convenience he assumes here that the labour generates the same OI(t) in the production of all products. Thus De Wolff concludes, that in the optimum of the Robinson person one has LIn = LIm = OI, for two products n and m. In the nineth chapter of Het Economisch Getij De Wolff now crowns it all, by applying his findings for the Robinsonade to the society as a whole15. For he considers a society of individuals n (say with n=1, ..., N), who each make a product n. This is a division of labour, where each person specializes in a single product. Then the relation of intensities at the optimum topt just mentioned simplifies into:
(5) LIn(n, topt) = OI(n, topt)
These intensities are not by definition equal to LIm(n), because n is not involved in the generation of the product m. It is obvious that each individual prefers to make the product, for which his labour productivity apn is the most competitive in comparison with the other individuals. However, De Wolff assumes that all individuals have the same apn. Then it is irrelevant who makes a certain product, and if desired two individuals are free to swap positions in the social production process16. Next all individuals start to exchange their products on the markets, hoping that the transaction enlarges their own lust (utility). It is generally known, that in such markets the second law of Gossen holds. For an individual k and two products n and m the law is17:
(6) LIn(k) / LIm(k) = pn / pm
In the formula 6 the quantities pn and pm are intepreted as the prices of the products n and m. In other words, the exchange proportion equals the ratio of the lust intensities. De Wolff combines the formulas 5 and 6 into
(7) OI(n) / LIm(n) = pn / pm
The formula 7 expresses that thanks to the option of exchange the optimal marginal disutility OI(n, topt) depends in part on the preferences for the other products m. The resemblance with the formula 4 is striking. Conversely the formula 7 has the peculiarity, that the price pn of the product n is related to the onlust intensity (the marginal onlust, or disutility) caused by its production. This reminds somewhat of the labour theory of value of Marx, where the price depends on the amount of expended labour time. The product price is determined by the workload, en not by the value of leisure time.
The formula 7 becomes even nicer, if the individual n is replaced by a representative (average) worker. For in that case all individuales have one single preference. This implies that one has LIm(n) = LIm(m). Besides the formula 5 states, that one has LIm(m) = OI(m). In combination these relations result in LIm(n) = OI(m). Substitution in the formula 7 results in18
(8) OI(n) / OI(m) = pn / pm
This formula 8 truly conforms to the marxist tradition. For now the exchange proportions are determined completely by the ratio of the marginal disutilities of labour. The prices are no longer determined by the needs of the consumers, but by the onlust of the workers. De Wolff revives Marx in a mannier, which is unique in the economic science, as far as your columnist can see.