Annotations concerning the LTV of de Wolff

First insertion on Heterodoxe Gazet Sam de Wolff: 11 may 2012

Labour time

At the beginning of the twentieth century Sam de Wolff developped his own version of the labour theory of value (LTV), which may be called interesting and original¹. However, De Wolff has not found the time, at least in his main work Het Economisch Getij, to elaborate on the consequences of his model. The present column has the aim to make a first start. The starting-point is the model, that has been formulated in two preceding columns. In the first column an economy of demand and supply is modelled in its simplest form. The second column extends this model to an economy with a variety of products. This is commented in the present column. It will be supplemented with a description of the opinion, that De Wolff gives on the various types of labour. De Wolff gives only a summary explanation of his opinion on these types of labour, so that it makes sense to annotate them in the present column. Therefore the column is less a description of the findings of de Wolff than an argument about the model of De Wolff.

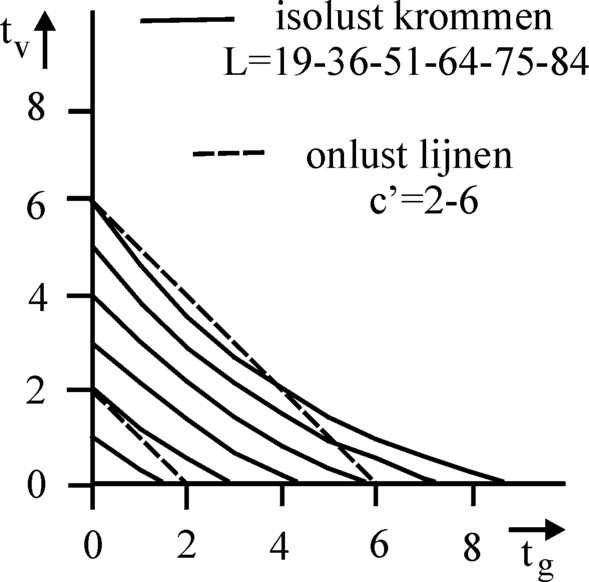
In the model of de Wolff the labour time t has several functions. Firstly, she determines the desire of the consumer for a certain product. The pleasure L of the consumer increases according as he obtains a larger quantity X of that product. The labour productivity ap relates the quantity X in a natural manner to the amount of labour time t_X, which is spent for its production². As a consequence the pleasure L for that product is a function of the labour time: L = L(t_X). Here the functional relation is not dynamic, but just a statement beforehand (ex ante): the consumer knows the pleasure L, which he experiences thanks to the quantity X, going with the time t_X. For the consumer the pleasure L and the related t are in the first instance static. This can be seen clearly from the fact, that the pleasure of the consumer is not affected by the time of acquisition of the products. Usually he will be contented, when he acquires his wage goods all at once at the end of his working day. In general his pleasure will not increase, when he for instance receives the fish before the corn. If these two products are offered on the market, then fixed iso-pleasure curves can be drawn in the (t_g, t_v) plane. The curves express a potential pleasure, which can be satisfied only by (the income of) performed labour.

Secondly, the labour time t determines the effort of labour, that the producer is willing to supply. The accomplishment of labour leads to a certain disutility, a displeasure O(t), which increases with the duration of the work. In case that the producer, also worker, disposes of self-knowledge, he will of course foresee his displeasure. But yet the labour time t confronts the producer with more dynamics than the consumer. In the production the labour time seems to advance, and so she is not static. In the eyes of the worker the last hour of labour is not equal to the first hour, for during the day the labour will become a heavier burden. The continuation of this column will show, that the succession of hours is especially relevant in situations with different types of labour. Moreover the labour is a succession of decisions: the worker must always decide, whether he wants to enlarge his purchasing power by working longer. A higher income promises a larger pleasure for the worker, in his role as consumer, but to him this increase seems to be realized by his labour. For during the labour the income is earned, or at least a claim on material goods.

Certainly an ideologist like Sam de Wolff must have developped his theory of labour value for a political purpose. He does not engage in this analysis out of purely scientific curiosity. It is obvious that he wants to use the displeasure of labour as an argument for the reduction of labour time, an for fair breaks, more holidays, and an early retirement³.

Displeasure

In the model of De Wolff the displeasure O is dependent on the labour time in a specific way⁴

(1)     O(t) = p₁×t + p₂×t² + p₃×t³ + ...

The formula 1 guarantees that the displeasure is zero as long as the worker remains idle. In a sense the formula deviates from the convention in the traditional labour theory of value. The traditional LTV assumes, that each working hour adds the same amount of value to the product, on which it is spent. So the value of the product increases in proportion to the spent labour time t. In the formula 1 the first working hour yields generally less displeasure than for instance the fifth working hour. For the exponent n of tⁿ pushes up the displeasure in an exponential way. This can also be seen by calculating the displeasure intensity OI(t), in other words the displeasure of the last produced amount of product⁵:

(2)     OI(t) = p₁ + 2×p₂×t + 3×p₃×t² + ...

The formula 2 shows that in general the displeasure due to the last produced unit of the good is larger than for its predecessor. It is obvious that the worker wants a larger hourly wage in compensation for his larger displeasure. Even if the hourly wage is averaged over the duration of the entire working day (8 hours), then it may still be expected that overtime will demand a higher reward. This suggests that overtime could push up the piece-wage of the good, and thus its price or value. In any case it is a fact, that in the subjective experience of the worker the later produced units have a higher price.

The economic production

In the Robinsonade the consumer and the producer are the same person. When the pleasure of the consumer and the displeasure of the producer are known, the person can calculate his optimal working time. This can be gone over in the first column, where the calculation is illustrated with an example. Note that in this simple case the requirement LI=LO is identical to the optimization of the difference L−O, so to ∂(L−O)/∂t = 0. Here the displeasure is a negative pleasure. It implies, that if desired the theory could replace the displeasure of labour by the pleasure of leisure time⁶. In the second column a more interesting case is studied, because she can be compared directly with the methods from the theory of marginal utility. Consider again the two pleasure functions in the example of that column. There a combined pleasure intensity LI(t) is constructed from the two pleasure functions. Now suppose that the displeasure of labour is given by

(3)     O(t) = ½×t²

Then the intensity of displeasure is given by OI(t) = t. The most economic (optimal) production is found by determining the intersection of the combined pleasure intensity LI(t) and the displeasure intensity OI(t) of formula 3. Following De Wolff one finds with these formulas, or from the figure, that the intersection occurs at t=9³/₅ working hours. This is the time, that the person is willing to work. A part of 4²/₅ hours is spent on the harvest of corn, and 5¹/₅ on fishing.

Figure 1: Iso-pleasure curves for corn and fish

However the shape of the combined pleasure intensity can be presented more clearly. Here the application of the methods from the familiar theory of marginal utility is helpful. Two pleasure can be simply added, because De Wolff uses a cardinal analysis of pleasure. The combined pleasure is

(4)     L(t_g, t_v) = L_g(t_g) + L_v(t_v) = 14×t_g - ½×t_g² + 20×t_v - t_v²

The figure 1 is a graphical display of the formula 4 in the (t_g, t_v) plane. The curves are so-called iso-pleasure curves, where the pleasure is equal, or to put it differently, the pleasure is constant. In the theory of marginal utility a similar figure is used for the determination of the optimal consumption with a given budget. Then the figure displays the so-called iso-utility curves (curves where the utility is constant), together with the budget line (the possible combinations of products, that can be bought with the given budget)⁷. In the model of De Wolff the analogy is the displeasure line. In this case the displeasure line represents the constant displeasure O(t)=c. Because of the formula 3 one finds ½×t² = c, and thus t=c' (with c' = √(2×c)). Note that a part t_g of the working time t is spent on the harvest of corn, and the other part t_v on fishery. It follows that t_g+t_v = c' must be true, or t_v = c' − t_g. This is a straight line in the (t_g, t_v) plane. If desired c or c' can be interpreted as the budget of displeasure, that is owned by the person.

The method, which is used in the theory of marginal utility for the calculations of the optimal consumption at a given budget, is adapted in the model of De Wolff in the following way. First the slope of the displeasure line is determined, so (dt_v/dt_g)_O. Here dt is an infinitisimal time step. Then the iso-pleasure curve is identified, which just touches the displeasure line. So there the slope (dt_v/dt_g)_I of the iso-pleasure curve is equal to the slope of the displeasure line. Only one such iso-pleasure curve exists, because iso-pleasure curves can not intersect each other. Then the point of tangency (t_g, t_v)_r is the desired optimal solution. The consequences of this method can readily be identified. Just now it has been shown, that the slope of the displeasure line equals -1. On an iso-pleasure curve one has dL(t_g, t_v) = 0. In other words, L does not change along the curve. Substitution of the formula 4 in dL=0 yields the expression (∂L_g/∂t_g) × dt_g + (∂L_v/∂t_v) × dt_v = 0. So LI_g × dt_g + LI_v × dt_v = 0. It follows from this, that the slope of the iso-pleasure curve (dt_v/dt_g)_I is equal to -LI_g/LI_v. In the point of tangency, that (as said) represents the optimal combination of products, this slope is equal to the slope of the displeasure line. So -LI_g/LI_v = -1, so that LI_g = LI_v. This is just the condition, that is used by De Wolff for the construction of his combined pleasure intensity. Thus it is proven, that indeed the method of De Wolff and the method of the theory of marginal utility yield the same allocation of the available labour over the two product branches. As said, the amount of labour, which the Robinson person makes available in total, depends also on his intensity of displeasure OI.

Various types of labour

De Wolff is seduced by his ambition to consider also the case, where each type of labour carries its own displeasure. Then the harvest of corn and the fishery each have their own function of displeasure, still in the form of the formula 1, but with different coefficients p₁, p₂, ... . Indeed the traditional labour theory of value acknowledges, that each type of labour requires its own particular effort, because it needs a specific knowledge and skill. Nevertheless it is commonly assumed, that the effect of the differences in labour are of minor importance. Therefore De Wolff could with a clear conscience have ended his model here.

Figure 2: Coupling two types of displeasure

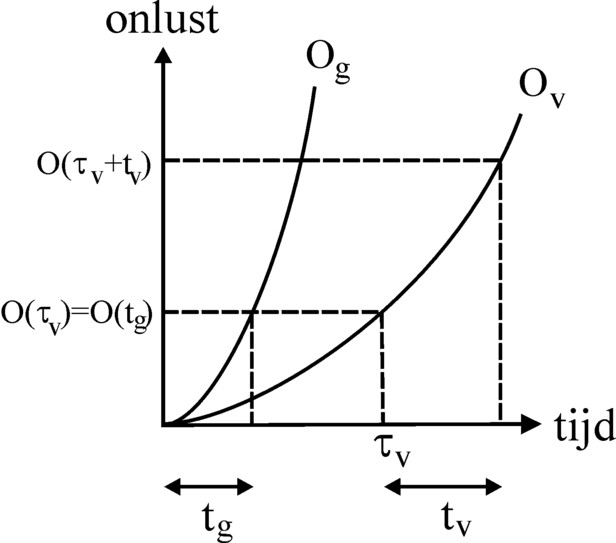
This new refinement confronts him with the question how the various displeasures O(t) should be added. In the formula 4 a cardinal addition is performed, because it is irrelevant for the pleasure of the Robinson person whether the corn is obtained first, or the fish. Unfortunately the cardinal addition does not hold for the displeasure. For when someone has fished for a number of hours, he will keep his fatigue during the succeeding harvest of corn. In his subjective perspective the harvest does not start at t_g=0, for he has a past of work, and thus there is a sequence. Therefore a complicated question arises: suppose the Robinson person wants to reach with his labour a certain point in the (t_g, t_v) plane, because he strives for the corresponding pleasure (see the figure 1). Then how should he divide his working day in order to experience a minimal displeasure? Which trajectory should he pass through in the (t_g, t_v) plane? Should he harvest first, or should he start with fishing? This is by no means a trivial question⁸.

De Wolff does not really dwell on these dilemmas. He simply assumes ("It is plausible") that the total displeasure is independent on the sequence, in which the production is carried out⁹. His method is as follows: suppose first there is a harvest of corn during a time t_g. The corresponding displeasure is O_g(t_g). Then the same person continues with fishing during a time t_v. His displeasure at the beginning of the fishing can be interpreted as a displeasure O_v(τ_v), where it seems as if he has already fished during a time τ_v. The time τ_v can be calculated from the equation O_g(t_g) = O_v(τ_v). At the end of his working day the displeasure of the person is equal to O_v(τ_v + t_v). The figure 2 shows graphically how the method of De Wolff works.

A similar argument can be used, when the person starts with fishing during a time t_v, followed by a time t_g of harvesting. In this case his displeasure at the end of the working day is equal to O_g(τ_g + t_g). Thus the method of De Wolff can be summarized in three formulas:

(5a)     O_v(τ_v) = O_g(t_g)
(5b)     O_g(τ_g) = O_v(t_v)
(5c)     O_v(τ_v + t_v) = O_g(τ_g + t_g)


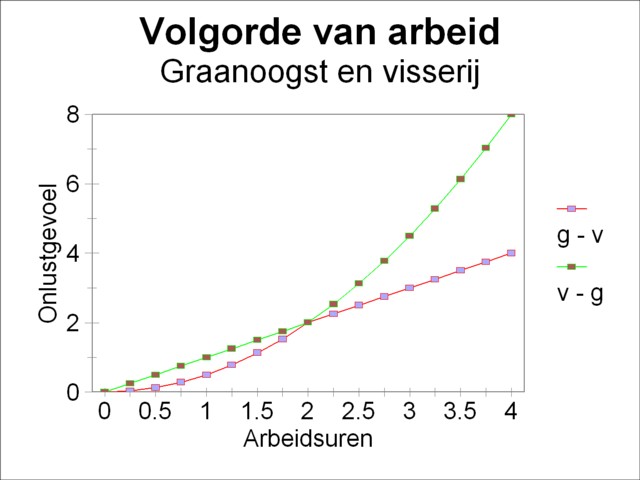
Figure 3: Displeasure of non interchangeable labour The three formulas 5a-b-c impose a considerable restriction on the possible forms of the displeasure functions of the formula 1. De Wolff proves that due to the requirements 5a-b-c the coefficients in the formula 1 have to satisfy¹⁰

(6)     (p_n)_v = (p_n)_g × ((p₁)_v / (p₁)_g)ⁿ   for n=1, 2, 3, ...

The formula 6 defines when the sequence for the performance of two types of labour can be exchanged without consequences. An example may clarify this. Suppose one has O_g(t_g) = ½×t_g² en O_v(t_v) = t_v. Here (p₂)_g=½ and all other (p_n)_g are equal to zero, (p₁)_v=1, and all other (p_n)_v are equal to zero. Evidently the coefficients in this example differ from the formula 6, so that in this situation the types of labour should not be interchangeable. In fact the formulas 5a-b show that τ_v = ½×t_g² and τ_g = √(2×t_v). Substitution in the left hand side of the formula 5c yields O_v(τ_v + t_v) = τ_v + t_v. However, substitution in the right hand side yields O_g(τ_g + t_g) = τ_v + t_v + 2×√(τ_v × t_v). Then the left and right hand side of the formula 5c are unequal. The figure 3 shows this also in a graphical way (with t_g = t_v = 2 working hours). Dependent on the sequence of labour the displeasure in this figure is equal to 4 or 8. Indeed the system of displeasure O_g(t_g) = ½×t_g² and O_v(t_v) = t_v does not permit an exchange. So according to De Wolff such systems of displeasure are not plausible.

Now De Wolff again tries to find the most economic production. If your columnist understands him well, he uses the following argument. On the one hand the Robinson person experiences at the end of the working day a displeasure O_v(τ_v + t_v). At that moment the displeasure intensity for fishing is equal to OI_v(τ_v + t_v). There is a balance, when this displeasure intensity is just balanced by the pleasure intensity for the quantity of fish, that is obtained during the day. For if the pleasure intensity would be greater, then the person would continue to fish. That is to say,

(7a)     OI_v(τ_v + t_v) = LI_v(t_v)

Using the same argument De Wolff finds for the corn the requirement

(7b)     OI_g(τ_g + t_g) = LI_g(t_g)

De Wolff words it like this: "Here the rule holds, that the intensity balances (columnist: those are (LI − OI)_g and (LI − OI)_v) are zero for each good, or the ratios of intensities (columnist: those are (LI / OI)_g en (LI / OI)_v) are equal to 1"¹¹. This marks the most economic production. So although the ratios of intensities are all identical, and due to the formula 5c also the displeasures, this does not hold for the pleasure intensities. In general LI_g(t_g) will differ from LI_v(t_v).

De Wolff illustrates his method with an example. He puts O_g(t_g) = ½×t_g² and O_v(t_v) = 2×t_v². It can simply be seen, that these displeasures obey the formulas 5a-b-c. It follows that τ_g = 2×t_v and τ_v = ½×t_g. De Wolff uses for the pleasure again the formula 4. Using the formulas 7a-b one finds after some simple calculations, that the economic production must obey t_g = 5½ working hours and t_v = 1½ working hours. Apparently in this situation the Robinson person chooses a total working day with a duration of 7 working hours¹².

Previous columns on this portal have shown, that De Wolff is not afraid to present bold assumptions as a truism, and to defend them spiritedly. Nevertheless your columnist is by no means convinced that the assumptions 5a-b-c and 7a-b of De Wolff are really plausible. But if they are accepted, then they provide for a complete LTV model for the calculation of the optimal production in an economic system with two branches. Your columnist would certainly for the previous text welcome suggestions for improvements, additions and other remarks.

1. Some time ago, after writing this column, your columnist discovered on internet the paper Gossens Theorie der Zeitallokation im Lichte neuerer Theorien (2000) by Daniel Dohrn, from the university of Munich. Here Dohrn interprets the theory of Hermann Heinrich Gossen, and presents a formalism, which is almost identical to the model of De Wolff. Although your columnist has not read the original book of Gossen, the paper of Dohrn is an indication, that De Wolff is actually inspired by Gossen. (back)
2. After writing this column, your columnist acquired the thesis Over marxistische economie in Nederland (1993, Thesis Publishers Amsterdam) by F. Kalshoven. In chapter 4 he discusses the work of Sam de Wolff. Kalshoven states that the neoclassical text of De Wolff is first published in 1925, in the magazine De Socialistische Gids. On p.179 of his thesis Kalshoven prefers to interpret the tranformation from quantities to time as a production function X = f(t). But for the rest Kalshoven does not analyse this part of the model of De Wolff. Kalshoven discusses mainly the exchange model of goods, which is also presented in De Socialistische Gids of 1925, and which is reprinted in chapter 9 of Het economisch getij. Perhaps this deserves a separate column, since here De Wolff completes his LTV. He derives a variant of the Second Law of Gossen, where the prices of goods are related to the displeasure of the individuals. (back)
3. If the model of De Wolff is applied in this way, then is should be remembered, that often the worker can influence his displeasure. Notably he can decide to reduce the labour intensity during the day (at least, if he is not totally integrated in the production process, such as with an assembly line). His labour productivity ap will decrease. In other words, during the day the worker redefines the type of work in his branch. This should be taken into account, for instance in the indifference curves. They are only valid, as long as the ap is stable. (back)
4. This expression can be found on p.445, in the appendix of Het Economisch Getij. (back)
5. For convenience it is assumed that the unit is very small. Then OI(t) is simply the derivative of O(t), so OI(t) = ∂O/∂t. (back)
6. Your columnist is not a labour economist. But the excellent textbook Volkswirtschafstlehre (2003, Oldenbourg Wissenschafstverlag GmbH), by M. Heine and H. Herr, treats on p.121 and further the leisure time as a utility good. Then the decision about the amount of working time becomes a part of the consumer theory. At the same time in this way the succession of periods of working time disappears from the model. No conclusions can be made concerning the form, that the leisure time should have: longer breaks, a shorter working week, more holidays, or an early retirement. Your columnist has the impression that the concept of the intensity of displeasure originates from Jevons (marginal disutility of labour). The concept of the pleasure intensity (marginal utility) of the leisure time seems to originate from the Austrian School. (back)
7. The theory of the consumer utility can be read over in the book Volkswirtschafstlehre just mentionned, in the Dutch book Micro-economie (1996, Stenfert Kroese), by F.J. Dietz, W.J.M. Heijman, and E.P. Kroese, or any other decent book about general economics. (back)
8. Perhaps the phenomenon clarified by comparing two very different types of labour. Suppose for instance that the Robinson person wants to both carry sacks of corn and repare watches on a daily basis. If he starts with the displacement of sacks, he might afterwards miss the steady hand of the watchmaker. If he starts with the reparation of watches, he might afterwards be too exhausted to displace sacks of corn during several hours. (back)
9. On p.445 in the annex of his work het Economisch Getij he writes (in translation): "Now we introduce the assumption (incidentally very plausible) of interchangeable succeeding types of labour. In other words, it is irrelevant whether the first x working hours are in the former branch, and subsequently y hours in the latter branch, or first y hours in the latter and then x hours in the former". (back)
10. De Wolff argues as follows: consider working days, where the harvest takes t_g hours and the fishing takes t_v hours, with t_g and t_v chosen in such a way that O_v(t_v) = O_g(t_g). That is to say, for this t_g and t_v the formulas 5a and 5b coincide. Then it follows from the formula 5c that O_v(2×t_v) = O_g(2×t_g), and more generally O_v(k×t_v) = O_g(k×t_g), with k=1, 2, 3, ... . Substitution of the formula 1 in the formula 5c yields k × ((p₁)_g×t_g − (p₁)_v×t_v) + k² × ((p₂)_g×(t_g)² − (p₂)_v×(t_v)²) + ... = 0 for k = 1, 2, 3, ... . This is only possible, when in this formula all coefficients of the power kⁿ are equal to zero. Thus (p_n)_g×(t_g)ⁿ − (p_n)_v×(t_v)ⁿ = 0 for all n. When in this formula the expression (p₁)_g×t_g = (p₁)_v×t_v is used to divide out the times, then on obtains the formula 6. (back)
11. See p.331 of Het Economisch Getij. (back)
12. On p.331-332 of Het Economisch Getij De Wolff considers the case of rational production with t_g = 5 working-hours and t_v = 1 workig-hour. There he concludes, that the intensity-surplus can not be identical for all articles. As far as your columnist can see, his calculation is wrong. He states that the intensity-surplus (LI − LO)_v equals 18. But that must be 16, because LO_v = 4. (back)