Fundamentals of welfare economics

First insertion on Heterodox Gazette Sam de Wolff: 2 august 2018

The present column describes several essential concepts and models of welfare economics. First the compensated demand curve, the consumer surplus, the rent of entrepreneurs, and the dead-weight loss are explained. Next, measures of social inequality are discussed. They are convenient in order to include the aversion against inequality in the social welfare function. The economist Binmore shows, that the latter inclusion can also be realized by combining the pure utilitarianism and the maximin principle of Rawls.

The individual demand curve

The consumer behaviour of the individual k is commonly determined by two factors: his preferences and his income y_k. Preferences can be modelled as a utility function u_k. The individual makes his choices from the assortment of products, which is available on the markets. Suppose that the market offers N differing consumer goods, with a market price p_n for product n. When saving is ignored, then the consumption of k is limited by the so-called budget line

(1)     y_k = Σ_n=1^N   p_n × q_n

Here q_n is the quantity of the product n, which is consumed by the individual k. Actually p_n and q_n are vectors with N elements each, so that for the sake of convenience the formula 1 can be represented by the inner product(p·q). The vector q transforms the income y_k in a basket of commodities. Common sense says, that q depends on p. For, expensive products are less desirable. The function q_n,k(p) is called the individual demand curve of the product n, in agreement with the preference of k. The form of the demand curve can be derived analytically. Namely, the individual k naturally tries to optimize the utility of his basket of commodities, within the limits of his income. The optimal composition is given by q_k^*. Incidentally, for the present discussion it is more clarifying to interpret the utility as the welfare of k. The consequence is, that q_k^* is determined by the utility function u_k(q) of k. For the sake of convenience the index k will be omitted in the notation.

Figure 1: (a) indifference curves and budget lines
    (b) normal demandcurve ψ, belonging to figure a

For the sake of clarity the analysis of the demand curve is commonly presented in two dimensions. In this way the problem can be shown as a graph. Thus the figure 1a presents the utility field u(q₁, q₂) of an economy with two products (N=2). Each red curve is an indifference curve of constant utility, with a rising welfare in the order u_a, u_b, and u_c. Now suppose that the product price p₁ of the product 1 is reduced in steps, with p_1,a > p_1,b > p_1,c. The price p₂ remains constant. This is actually a deflation, because the spending power per unit of money rises. Since the individual income y has a nominal value, in this situation the individual welfare increases. This phenomenon is shown in the figure 1a. The green lines are the budget lines for the same y, but at three different prices p₁. According as p₁ falls, the optimum q^* shifts: the individual gives up units of product 2 in order to acquire more units of product 1.

The process of optimization can be called a utility maximization problem, or an expenditure-minimization problem¹. Apparently two mechanisms are relevant. On the one hand there is substitution of the product 2 in favour of the product 1. The Gazette has paid attention many times to the substitution of production factors, and the same process occurs here for decisions about consumption. On the other hand, the individual can buy more of both products, because his real spending power has increased. Thanks to the extra spending power with a size of q₁ × Δp₁ the individual welfare obviously increases, from u_a to u_b and u_c. This second phenomenon is called the income effect. Within this frame, a convenient concept is the expenditure function, which is defined as e(p, u) = y(q^*). Although y remains constant, both p and u change.

The figure 1a is especially interesting, because for each value of p₁ the corresponding optimal q₁^* can be read. The resulting curve is shown in the figure 1b. This is called the normal demand curve ψ₁(p₁,y), or also the demand curve of Walras or Marshall². Note that in graphs the demand curve is often confusingly presented with q^* along the horizontal axis and p along the vertical one! This ignores the causality. Since ψ_n can be determined for all n products, it is actually a vector ψ. The function ψ plays an important role in the study of market processes, However, it is not suited for describing the development of welfare. For, in changes of p₁ the individual utility u varies in a complex manner.

Figure 2: (a) indifference curve and budget lines
    (b) compensated demandcurve φ, belonging to figure a

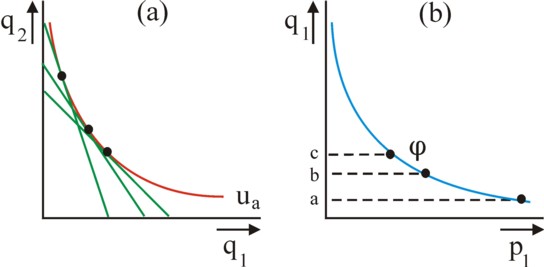
Therefore economists have invented an alternative demand curve, which has little practical relevance, but which is indispensable in welfare theory. Consider for this the figure 2a, which shows the indifference curve u_a. It has just become apparent, that the income y in combination with the product price p_1,a leads to the optimal consumption q_a^* on the curve u=u_a. This budget line is drawn in the figure 2a. Also all other points on the curve represent an optimum q^*, with the same utility u_a, but at another price p. As an illustration two are drawn, for p_1,b and p_1,c, with unchanged p₂. The three green lines are again budget lines, where however only q_a^* still has e(p,u) = y. For, the falling p₁ increases the spending power, so that the utility u_a only remains constant for a falling income e(p,u_a). The points on u=u_a define the compensated demand curve q₁^* = φ₁(p,u). This function is also called the demand curve of Hicks³.

The income y no longer appears in φ, because it naturally adapts to p₁ and u_a. For instance, the income falls between q_a^* and q_b^* with e(p_a,u_a) − e(p_b,u_a) ⁴. This is an abstraction, because actually the households and companies always have a budget limitation. The income effect is eliminated artificially from the theory. Therefore the price p can not be attributed here to the market process. In the compensated demand curve the individual does not optimize his basket of commodities, but expresses with p_n his personal appreciation for the product n. Then p_n is called the marginal evaluation, or the willingness to pay⁵. A simple use is made of the second law of Gossen, which states that the unit price matches the marginal utility. In formula: ∂u/∂q_n = λ×p_n, where the so-called marginal utility of the expenditure λ is a constant for all products n.

In other words, the acquisition of the product n is indifferent. The price and the individual (marginal) utility are balanced. An outsider can only measure the compensated demand curve φ by asking the individual about it. The function φ can be constructed from the utility field, with the same method, which has been applied in the figure 1 for the demand function ψ. Then the compensated demand curve in its common form is found. The result is shown in the figure 2b. Note that φ₁(p₁,u_a) falls in a less steep manner than ψ₁(p₁,y) ⁶. Now suppose, that the product n is offered for a unit price of π_n. Then the individual continues to buy units of the product, as long as π_n ≤ p_n holds. In other words, he obtains the units q_n = φ_n(π_n,u) at a lower price than his own valuation or willingness to pay. This yields him an extra utility or welfare, which is called the individual consumer surplus .

The total social surplus

The consumer surplus

The consumer surplus furthers the individual welfare, but the present column mainly addresses the social welfare. Then the social consumer surplus CS must be calculated. For this the social demand must be determined, by means of φ, because only this demand function indeed assumes a concrete utility value. Suppose that the society consists of K individuals. Introduce again the index k for the individual. Then the social demand function is calculated as

(2)     Φ_n(p,W) = Σ_k=1^K   φ_n,k(p,u_k)

Figure 3: Demand and supply:
    (a) consumer surplus and producer-rent
    (b) idem, with tax, with a dead-weight loss

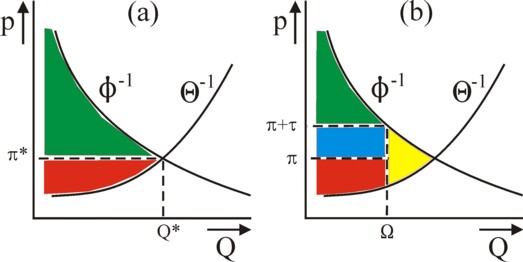
In the formula 2, W is the social welfare, which is a function W(u) of the utility vector u_k. The function Φ_n is equal to the social demand Q_n. The individual demand curves q_n,k are piled up, as it were. Incidentally, sometimes it is convenient to assume a representative individual, so that all individual demand curves are identical. Thanks to the function Φ_n(p,W) it can be analyzed to what extent the policy of the state reduces the welfare W. First, consider the common market situation. It is shown in the figure 3a, where in accordance with the common convention the product price is registered along the vertical axis. So in fact this cruve is p_n = Φ_n^-1(Q_n), where Φ^-1 is the inverse of the demand function. The welfare W is constant on Φ_n.

Next consider the producers. Call the function Q_n = Θ_n(p_n) their total supply-curve. The marginal production costs c_n are obviously a limiting factor for the size of the supply. The c_n are determined by the available equipment (the stock of capital goods), which is bounded. When the available production capacity is overloaded, then c_n(Q_n) will rise excessively. Then it is also necessary to work overtime, etcetera⁷. It is often assumed, that one has p_n=c_n, because thanks to competition on the markets the profits would be negligible. Then the function Θ_n rises for an increasing p_n, because the production costs can increase just like p_n. In other words, the social profit is constant on the curve Θ_n. In the figure 3a the inverse function Θ_n^-1 is shown. The demand and supply are identical at the equilibrium price π_n^*. In the equilibrium Q_n^* the markets clear.

Now the total consumer surplus CS can be read from the figure 3a. It is represented by the green area. It can be calculated as

(3)     CS(Q_n^*) = ∫₀^Q*  (Φ_n^-1(Q) − π_n^*) dQ_n

The private markets create the consumer surplus, which contributes to the welfare W. This completes the welfare analysis for the consumptive sphere⁸.

The total surplus

Next consider the situation of the producers. They have costs c_n = Θ_n^-1(Q), and these are below the product price π_n^*. Since the producers can demand π_n^* on the market, they apparently receive a producer rent PR. The rent is represented by the red area in the figure 3a. It can be calculated by means of an integration, just like the CS in the formula 3. The PR also contributes to the social welfare W ⁹. Thanks to the private market there is a total social surplus MS, which is the sum of the CS and PR. In other words, the MS is the total of the green and red area in the figure 3a. It can be calculated as

(4)     MS(Q_n^*) = ∫₀^Q*  (Φ_n^-1(Q) − Θ_n^-1(Q)) dQ_n

The effect of state intervention on welfare

The state is indispensable, because a regime must be created, which allows the private markets to prosper. But regimes also coerce, and therefore they lead to discontent and reduce welfare. A state intervention forces the individuals to change their behaviour, and this change often undermines the efficiency. A familiar example is the levying of taxes. They are indispensable, because the state must be paid, but they lead to much annoyance. Thanks to the theory of the social surplus the loss of welfare due to taxes can be depicted. Suppose that the state imposes a consumer tax τ_n on the acquisition of the product n (VAT, excise, import tariff). This raises the unit price to π_n+τ_n. The demand function Φ_n(p_n) shows, that then the consumed quantity decreases to Ω_n. This is shown graphically in the figure 3b.

Thanks to the tax the state receives a sum τ_n×Ω_n. See the blue area in the figure 3b. These benefits are at the cost of the consumers, who must give up a part of their consumer surplus CS for this. The tax does not affect the incomes π_n of the producers¹⁰. Thus it seems, as though the tax is socially neutral for the welfare W. However, both the CS and PR diminish, because due to the state intervention a quantity Q_n^* − Ω_n of the product n can no longer be sold. The incentive to consume has changed. This lost social welfare is called the dead-weight loss (DWL)¹¹. It corresponds to the yellow area in the figure 3b. It can be calculated with the formula¹²

(5)     DWL(τ_n) = ∫_Ω^Q*  (Φ_n^-1(Q) − Θ_n^-1(Q)) dQ_n

So it is important to compare the possible advantages of state interventions with the accompanying lost welfare. In this case the problem is fiscal. Similar problems occur in the income tax, because these actually lower the incomes¹³. Therefore the incentives to work or to save are attenuated. In principle taxes can be imposed without disturbing the economic behaviour of the individuals, namely when τ is a remittance of money, which is equal for all individuals. This is called a lump-sum, or a poll tax. This is to say, it is independent of economic behaviour, such as consuming or producing. However, the equal lump-sum for everybody can not be reconciled with feelings of justice and fairness. For, such a tax would increase the relative differences in income. The secondary distribution would become more unequal¹⁴.

Inequality in the social welfare function

Just now the social welfare function (in short SWF) has been introduced in the argument. A recent column has already discussed the first principles of this SWF. According to the spiritual fathers of this concept, A. Bergson and P.A. Samuelson, the SWF is simply the utility function of the central planning agency. The SWF can represent targets, but also norms and values. Often the SWF is moelled as a general utilitarian function, of the form

(6)     W(u) = Σ_k=1^K  g_k(u_k)

In the formula 6, there is a society of K members. The variable u_k is the yield of the member k (k=1, ..., K). Strictly speaking this yield is the individual utility of the welfare of k. However, the reader is warned, that some models also interpret u_k as purely material benefits. The function g_k is the weight, which is attributed to the interest of k by the central planning agency. It has yet to be defined more accurately, but in any case it satisfies ∂g_k/∂u_k > 0. This condition is self-evident. It guarantees, that the principle of collective growth of income has been satisfied. This is to say, when each individual k receives an additional constant yield Δu, then the social welfare W must increase. Besides, it guarantees that the principle of monotony has been satisfied. This is to say, when an individual k receives more yield Δu_k, whereas the other yields remain unchanged, then W must also rise¹⁵.

Moreover, the function W of the formula 6 satisfies the principle of strict independence within the society. This is to say, when in a subgroup of society one has W(u_s) > W(v_s) (where the two different utility vectors of the subgroup s are compared: u_s≠v_s), then this order remains unchanged, even when elsewhere in the society the yields change¹⁶. Thanks to the weight g_k, the SWF can model for instance a policy for target groups. However, for the sake of convenience it is often assumed, that g_k = g holds. Then the principle of anonimity is valid, so that no individual k is priviliged. All are mutually exchangeable. In other words, a permutation of the members k does not change the value of W ¹⁷.

Measures of social inequality

The social inequality is also important, besides the welfare W. Previously it has been argued in the Gazette, that the choice of the measure μ_I of inequality is subjective. Then it has already been suggested, that this measure can be coupled to the SWF. The argument is as follows. Suppose that there is indeed anonimity. Then the representative yield ω can be defined by means of the equation g(ω) = W/K. Therefore ω can be calculated from g^-1(W/K), where g^-1 is the inverse function of g. Define also the average yield as ν = Σ_k=1^K  u_k/K. Now there are two plausible measures of inequality¹⁸

(7a)     μ_Ia = g(ν) − g(ω)
(7b)     μ_Ib = 1 − ω/ν

These measures of inequality differ, because μ_Ia depends on the total yield K×ν. On the other hand, μ_Ib is based on the ratio of ν and ω, so that the scaling effect of an increasing yield is absent. It is desirable, that the measure of inequality is normalized¹⁹. This is to say, one must have μ_I=0, when u_k=ν holds for all k. Moreover one has μ_I(α×u) = μ_I(u) for an arbitrary scalar α. So this invariance for scaling does not hold for μ_Ia ²⁰. And finally μ_I remains unchanged, when the society expands with copies of itself. In other words, each individual k can be interpreted as a group with n members.

The measures μ_Ia and μ_Ib are especially important for the case ∂²g/∂u_k² < 0. Such a function g is called concave²¹. Then the utility of an extra yield Δu_k decreases, at least for the society, according as u_k is larger. Under this condition SWF W(u) expresses an aversion against inequality²². Thus the desire for levelling is included in the model. This step uses the psychological insight, that unfair inequalities indeed cause discontent with the harmed people. When the SWF attaches a value to the inequality, then it can be represented by W = W(ν, μ_I, K) ²³. So this function takes into account inequality and K×ν, the total unweighed ("material") yield. Now the form of g(u_k) is important. Note already now, that the pure utilitarian weight g(u_k) = u_k does not satisfy inequality aversion. This type of W remains unchanged after a redistribution from the poor to the rich.

The theory of measures μ_I provides for the insights, which allow to find an appropriate g(u_k). For this define two extra principles²⁴. The principle of the transfers states: when yield is transferred from an individual to a richer individual, then the measure μ_I must indicate, that the distribution of yields has become less equal. Such a transfer does not change the average ν, but it does decrease the representative yield ω. Therefore for instance the value of the measure μ_Ib will increase, because ω/ν decreases. Moreover, introduce a second principle of independence. Namely, in a subgroup s of the society the measure μ_i(u_s) must always establish the same order among the various utility distributions u_s, irrespective of the yields in the rest of the society. Now the four principles of inequality (anonimity, irrelevance of scale, transfers and independence) lead to a unique function of equality²⁵:

(8)     f(u, θ) = Σ_k=1^K  u_k^θ

In the derivation of the formula 8 a constant total yield K×ν is assumed. The scalar θ is a parameter, which must not be θ=0 or 1 ²⁶. The function f has the property, that it assumes the extreme value (K×ν^θ) for complete equality u_k=ν for all k. Apparently it is not normalized. When θ<1 holds, then other utility distributions are valued higher. Now complete inequality is the minimum of f.

Furthermore the choice of θ determines the specific sensitivity of the function f. For instance, when θ→-∞ holds, then the value of f is determined completely by the smallest u_k. More generally, for low values of θ, f attaches the largest weight to the lowest yields u_k in the evaluation of inequality. Conversely, for high values of θ (much larger than 1) the evaluation of inequality mainly weighs the largest yields u_k. The influence of θ is naturally a problem, because thus there exists an infinite number of measures μ_I of inequality. The choice of a certain measure is in essence subjective. Everybody could select the measure, which pleases him or her the most. Some will mainly value the utility of the poorest, whereas others attach more weight to the inequality in the middle class. In other words, the choice of θ determines which subgroup is analyzed. With such a flexible measure it is evidently impossible to engage in science!

Synthesis of measure and welfare function

The function f is actually used in the derivation of a measure μ_I of inequality. However, a clever find is to base the SWF itself on this function f of equality. A logical choice is g(u_k) = β×u_k^θ, where β is a scalar. Then the SWF equals β×f! The principle of monotony requires, that β depends on θ. In the literature one finds β=θ or β=1/θ ²⁷. When W must express an aversion against inequality, then it must be concave. The choice g(u_k) = β×u_k^θ implies θ<1. Then the welfare indeed increases as a result of levelling. Moreover, this emphasizes the position of the poor. In the extreme case θ→-∞, W even represents the maximin principle of Rawls. Apparently θ characterizes the aversion against inequality. Furthermore, note that the social welfare rises with α^θ, when the yields grow with a factor α. The grow clearly satisfies the principle of the collective growth of income.

Choose the utility scaling β=θ. The SWF can also be characterized by calculating the elasticity ε_uk of its marginal utility ∂W/∂u_k ²⁸. It is given by

(9)     ε_uk = ∂²W/∂u_k² / (∂W/∂u_k / u_k)

This elasticity will usually depend on u_k. But for the selected W it turns out that one has ∂W/∂u_k = ∂g/∂u_k = θ×g / u_k, and ∂²W/∂u_k² = ∂²g/∂u_k² = θ×(θ-1) × g/u_k². Apparently the elasticity of the marginal utility ∂W/∂u_k has the constant value ε_uk = θ-1. It is negative for θ<1. As a result of an increase of the utility (or the yield in the terms of the present column) u_k with 1% the marginal utility of W (the growth of the social welfare) decreases by (θ-1)%, irrespective of the value of u_k. Functions with this property have a constant elasticity of substitution, and therefore are called CES functions.

A complication of the selected g function is, that for θ<0 the SWF is negative. Then a complete levelling u_k=ν leads to the smallest possible negative value of W, for the concerned total yield. It is more clarifying to use a positive SWF. A good choice is the representative yield ω, which is found after a one-to-one transformation of W ²⁹. One has g(ω) = θ×ω^θ = W/K, and from this it follows

(10)     ω = (Σ_k=1^K  u_k^θ / K)^1/θ

Note that for complete equality u_k=ν holds for all k, so that in this point ω assumes the value ν. As long as θ>0, ω is positive for all u≠0. When θ<0, then one has ω=0 as soon as any u_k=0. Then the aversion against inequality does not accept, that any individual is without yield³⁰. Furthermore it is interesting to analyze the welfare or the representative yield for various utility distributions, when the total yield is given. Especially the case with K=3 can be shown in a graphical manner³¹. For, then the distribution u has three dimensions and this can be drawn. Assume for the sake of convenience, that K×ν=1 holds. The budget plane of the society has the form u₁ + u₂ + u₃ = 1. This is shown in red in the figure 4a. There is a complete equality along the "ray" through the origin with direction vector (1, 1, 1). It intersects the budget plane in u_k = ν = ¹/₃.

Figure 4: (a) budget plane;
    (b) indifference curves for θ=0.9,   (c) for θ=-1,   and (d) for θ=-10

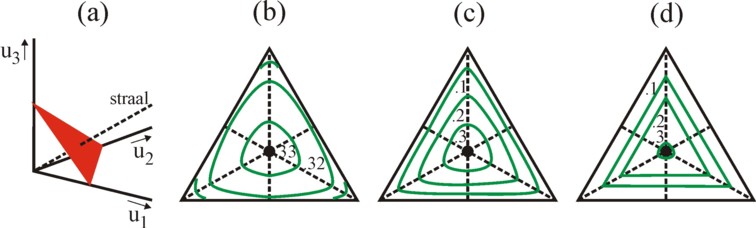
Since the yields are not negative, the budget plane remains restricted to the positive quadrant. Here the budget plane has the form of a triangle with equal sides. In this plane the indifference curves of the representative yield ω are drawn. The figures 4b, c and d show the indifference curves for respectively θ=0.9, θ=-1, and θ=-10 ³². In the figure 4b (θ=0.9) there is hardly aversion against inequality. Here ω varies between 0.295 (in the corner points) and 0.333. In the figures 4c-d θ is negative. At the edges of the triangle one always has at least one u_k=0, so that there ω=0 holds. The positive indifference curves also have a triangular shape, albeit with rounded corner points. In the figure 4d, ω falls relatively rapidly, according as the distance to the ray of equality increases. Here the indifference curves are mainly determined by the value of the lowest u_k. Therefore they are parallel to the edges of the triangle.

Although the figures 4b-c-d present the situation for the total yield 1, they also give an impression of the exchange between equality and the total welfare. Consider for instance in the figure 4c (θ=-1) the indifference curve ω=0.18. On the curve the smallest u_k has a value around ¹/₁₂ (0.0833), so that both other individuals share the rest with a size of ¹¹/₁₂ (0.917). The same representative yield can also be obtained in a completely equal society (situated on the ray) with ν = ω = 0.18. Here the total yield is merely 0.54, but the poorest individual more than doubles his yield. Apparently the total yield in the society of the figure 4c (with θ=-1) can be halved without punishment, as long as the yields are completely levelled! The reader may decide for himself whether this outcome is realistic³³.

Finally the measure of inequality must again be considered. The economist A.B. Atkinson has combined the formulas 7b and 10 in the derivation of his own measure μ_A. He defines η = 1-θ. Then his measure is

(11)     μ_A = 1 − (Σ_k=1^K ( u_k/ν)^1-η / K)^1/(1-η)

The reader may see, that this measure of Atkinson is based on an elegant theory. Its foundation is a series of well defined principles. The profound analysis is impressive. This is an advantage in comparison with empirical competitors, such as the coefficient G of Gini. Unfortunately μ_A suffers from the same indefiniteness of the parameter θ (and therefore of η). Moreover, although the theory is indeed elegant, its principles are quite controversial (although certainly reasonable). Policy analists know, that they must not get blinded by the intellectual excellence of models. This all probably explains, why in empirical studies the traditional intuitive measures such as G or the ratio of quantiles are still common, and not μ_A ³⁴.

Interpersonal comparison according to Binmore

The formula 10 for the social welfare uses an interpersonal comparison, where thanks to the parameter θ the importance of the lower yields weighs more heavily in the choice of policy. The economist K. Binmore presents in his book Playing fair (in short PF) another approach for targeted policies³⁵. He states that the social welfare function is given by (p.48, 294 in PF)³⁶

(12)     W(u) = Σ_k=1^K  α_k × u_k

The parameters α_k are constants. The welfare function W in the formula 12 is purely utilitarian. There clearly is no anonimity. Binmore assumes, that each individual k measures his yield u_k by means of his own utility scale, and calls the unit an util (p.54 in PF). The utils of different individuals k are not automatically equal. Now politics must determine the weights, which are attached to the interests of different individuals k. This is done by means of the ratio α_m/α_n, which values an util of m in utils of n. In other words, α_m/α_n is a conversion factor or exchange rate of utils. The exchange rate expresses, that an interpersonal comparison is made between the interests of m and n ³⁷.

The Gazette has regularly concluded, that economists have reservations with respect to analyzing interpersonal differences. For, such an analysis requires morals, so that the theory is no longer value-free. However, Binmore makes plausible, that the interpersonal comparison is a common social phenomenon. Namely, life in a group requires, that the individual behaviour must be mutually coordinated. Since the group must be durable and balanced, the members try to avoid conflicts (p.57, 289 in PF). Therefore they are inclined to take into account the ideas and well-being of the others (p.56, 288). They use their capability to show empathy. Empathy furthers cooperation, and therefore Binmore assumes, that it offers an evolutionary advantage (p.58, 297). The capability to show empathy is genetically favoured.

Thanks to empathy it becomes possible to formulate shared preferences (p.290). Social institutions form, as well as collective morals³⁸. Morals are transferred by means of imitation and education (p.65). In the long run the morals naturally adapt to the social changes. The system follows a path of subsequent social equilibria (path dependency). But in the short term the collective morals are fixed. Thus Binmore believes, that a social consensus emerges with regard to the values of the exchange rates α_m/α_n. This consensus is indispensable for chosing the optimal social order from all conceivable options. This is illustrated in the figure 5.

Figure 5: set of utility-
    possibilities and welfare-
    functions of Harsanyi and Rawls

For the sake of convenience the figure 5 is limited to the 2-dimensional case. The red curve defines the area (u₁, u₂) of possible utility vectors. The outer border of the area is Pareto optimal. The social optimum must be selected somewhere on the Pareto border. Commonly the point is chosen, where the welfare line W(u) of the formula 12 touches the set of possible utility vectors. The figure 5 shows the welfare line in green. Binmore attributes this welfare line W_H to the economist Harsanyi. However, this W is neutral with respect to inequality. Therefore the citizens will also demand, that the maximin principle of the philosopher Rawls is satisfied.

This principle usually has a different optimum than pure utilitarianism. Namely, suppose that the minimal allowable yield of the individuals k=1 and 2 is given by ξ = (ξ₁, ξ₂) (p.48). This point defines the origin of the utility scale, and is shown in the figure 5. Since also here the utils of the individuals differ, and must be converted, the welfare function W_R according to Rawls equals

(13)     W(u) = minimim van (α₁ × (u₁ − ξ₁), α₂ × (u₂ − ξ₂))

Next the maximum of this minimal welfare W_R must be selected. In other words, none of these two values must be less than the other. So the maximum must lie on the line α₁ × (u₁−ξ₁) = α₂ × (u₂−ξ₂). This line is shown in blue in the figure 5. Now the find of Binmore is, that thanks to the empathy of the citizens the values α₁ and α₂ are chosen in such a way, that the optima of W_H and W_R exactly coincide on the Pareto border, in the point σ (p.88)³⁹. Thus Binmore presents an alternative way to model the aversion against inequality. He assumes, that the citizens together distinguish between apparent social groups and their interests. On the other hand, the approach with the parameter θ of inequality assumes, that low yields naturally obtain more weight. Then the mechanism of empathy, which leads to shared preferences, remains invisible⁴⁰.

1. Many remarks from the now following argument are copied from chapter 3 in the famous reference work Microeconomic theory (1995, Oxford University Press) by A. Mas-Colell, M.D. Whinston and J.R. Green. The explanation there is more precise and complete than the explanation in the present column, and is highly recommended to the attention of the reader. However, this much detail is superfluous for the moment. (back)
2. See p.51 and further in Microeconomic theory, or p.49 in Économie et finances publiques (2017, Economica) by L. Weber, M. Zarin-Nejadan, and A. Schönenberger (or many other books). (back)
3. See p.62 and further in Microeconomic theory. It is worth noting, that the name giver of the Gazette, Sam de Wolff, bases his model on a Robinsonade, where the market is completely absent. Therefore his labour theory of value uses a compensated demand curve. There is no income, but merely a lust for consumption, and disutility due to labour. (back)
4. Your columnist also came up with the following argument. One has y = (p·q). Then the first-order approximation is dy = p₁×dq₁ + p₂×dq₂ + q₁×dp₁ (p₂ is constant). On the curve u=u_a the second law of Gossen is valid, namely ∂u/∂q_n = λ×p_n with n=1 or 2. The parameter λ is constant for all products n, and is called the marginal utility of expenditure. Insertion leads to dy = du/λ + q₁×dp₁ = q₁×dp₁. This latter equality holds due to du=0 for a constant u_a. A decreasing p₁ implies a negative dp₁ and therefore a negative dy. Stiglitz shows on p.524 in Economics of the public sector (2000, W.W. Norton & Company, Inc.), that the state can use this price-effect for increasing the tax yield. To be concrete: a lump-sum (poll-tax) can yield more than a consumer tax, without extra taxing the welfare of the consumer!
   By the way, according to p.81 in Microeconomic theory, e(p,u) is itself a utility function. Namely, assume that p is constant. Then e measures the real spending power, and e and u are mutually uniquely coupled. (back)
5. See respectively p.46-47 in Économie et finances publiques, as well as p.105 in Economics of the public sector. In the first reference this is also called a monetary equivalent of utility. (back)
6. According to p.71 in Microeconomic theory the equation of Slutsky holds: ∂φ_n/∂p_m = ∂ψ_n/∂p_m + q_m × ∂ψ_n/∂y, with n≠m. Both ∂φ_n/∂p_m and ∂ψ_n/∂p_m are negative, and ∂ψ_n/∂y is positive. This latter term represents the income effect. So the slope of φ_n is less steep than the slope of ψ_n. Although the function φ itself can not be observed directly, the Slutsky equation shows, that at least its derivative can be calculated from the observable ψ. On p.108 in Economics of the public sector it is stated, that for the common consumer goods ψ and φ are almost equal, because the product price is much less than the income. Here your columnist has his doubts. First, the freely available income is less than the available (secondary) income, because many expenditures are inevitable (rent, various insurances, public utilities). Besides, according to behavioural economics, individuals are inclined to spread their total income over a series of separate categories ("money boxes"). And rebates, such as bundling ("two for the price of one"), have the effect, that the extra income is spent completely on the discounted product.
   On p.68 it is yet stated, that the compensated demand and the expenditure function are related φ_n = ∂e/∂p_n.
   Since here p_n is related to ∂u/∂q_n, the figure 2b actually represents the first law of Gossen, which predicts a falling marginal utility. (back)
7. Until now, the Gazette has paid little attention to the costs of the social production. Some words are devoted to it in the column about planned prices. The column about employment describes the costs at the level of the enterprise. The column about the AS-AD model shows, that the total supply curve p(Y) rises for an increasing use of the production capacity. The Gazette has naturally also discussed a large number of models of social growth, but these are intended for the long run, when the stock K of capital goods can be increased simply. Such models have been developed precisely for planning the stock K. (back)
8. It is a rather complex argument, notably due to the introduction of the compensated demand curve. The theory requires a sound insight in the utility concept. Therefore it took a long time, before the consumer surplus has been introduced on the Gazette, in the column about privatization. Seven years ago, when your columnist published the experimental reader Vooruitgang der economische wetenschap, he still believed that the idea of the consumer surplus was not logical (in a footnote of paragraph 7.2). This qualification is caused by the fact, that at the time your columnist had the wrong belief, that the normal demand curve must be used. Even now he can barely imagine a balanced market, which has been stripped of income effects. The confusion is also caused by the deficient explanation in introductory textbooks. Some examples: Volkswirtschaftslehre (2003, R. Oldenburg Verlag) by M. Heine and H. Herr does not mention the compensated demand and the surplus. On p.451-453 van Handboek economie (1978, Het Spectrum B.V.) by P.A. Samuelson and p.73-74 of Grundzüge der Volkswirtschaftslehre (2011, Pearson Studium) by P. Bofinger the surplus does receive attention, but not the compensated demand. On p.69-71 in Microéconomie (1991, Presses Universitaires de France) by F. Etner and p.78-79 and 100 of Inleiding tot de economische wetenschap (1969, N.V. Uitgeversmaatschappij v/h G. Delwel) by G.Th.J. Delfgaauw both the surplus and the compensated demand are explained. Incidentally, Delfgaauw writes about a premium instead of a surplus. The book Microeconomie (1996, Stenfert Kroese) by F.J. Dietz, W.J.M. Heijman and E.P.Kroese merely mentions welfare economics in passing. Yet it excels, with an explanation of the income effect on p.185, of the willingness to pay on p.620, and of the consumer surplus on p.622. (back)
9. See p.529 and further in Economics of the public sector, or p.50 and further in Économie et finances publiques. Chapter 3 in De prijs van gelijkheid (2015, Prometheus - Bert Bakker) by B. Jacobs discusses the same theme, but with an application on the labour market. Then the enterprises are the demand side. (back)
10. On p.52 in De prijs van gelijkheid Jacobs remarks, that a clever state will also demand a part of the producer rent RP. For, at a production volume of Ω_n the marginal production costs c_n are less than π_n. So the state can tax the producers with (π_n − c_n(Ω_n)) × Ω_n. (back)
11. This is also called the triangle of Harberger, the inventor of the DWL. Another expression is the excess burden. On p.54 in Économie et finances publiques the DWL is called a perte sèche. On p.214 in Öffentliche Finanzen in der Demokratie (2011, Verlag Franz Vahlen GmbH) by C.B. Blankart this is called an Überschussbelastung. Here the surplus is called a Rente. This book mentions the income effect only in passing in a footnote, on p.214, although this is yet essential for understanding the DWL! (back)
12. On p.84 in Microeconomic theory the calculation of the DWL by means of an integration over p_n is (actually rightly so) preferred. This is an exception in the current literature, which prefers the method of the formula 5. For the sake of convenience assume, that the marginal costs c_n are constant, and equal to π_n. Then the producers will generate any desired quantity Q_n. For this they do not receive a producer rent. In the figure 3a, Θ_n^-1 is now a horizontal line at p_n=π_n. The result is DWL(τ_n) = ∫_π^π+τ  Φ_n(p) dp_n − τ_n×Ω_n = ∫_π^π+τ  (∂e/∂p_n) dp_n − τ_n×Ω_n = e(π_n + τ_n, W) − e(π_n, W) − τ_n×Ω_n. The term e(π_n, W) − e(π_n + τ_n, W) is called the equivalent variation (p.84). This formula explicitely shows, that the DWL is measured in units of money. On p.81 it is indeed stated, that e(p, W) is a money metric. Actually, the found form of DWL is logical. For, the welfare W only is conserved, as long as the loss DWL and the raised taxes are compensated by an extra income. The authors of Microeconomic theory merely mention the consumer surplus CS in passing. On p.89 they also calculate CS by means of an integration over p_n. (back)
13. This theme is central in the interesting Dutch book De prijs van gelijkheid. Jacobs mainly analyzes the income tax as an instrument for the redistribution of incomes. Your columnist will definitely return to this politically controversial theme. (back)
14. It is strange, that welfare economics advocates such a controversial instrument as the poll-tax. For, the marginal utility of income is larger for poorer people. Your columnist wonders, whether this outcome is caused by eliminating the income effect from the model. (back)
15. See for these two principles p.103 in Economic inequality and income distribution (1998, Cambridge University Press) by D.G. Champernowne and F.A. Cowell. Your columnist has the impression, that the principle of monotony is identical to the Pareto criterion. See p.825 in Microeconomic theory. (back)
16. See p.103 in Economic inequality and income distribution. Unfortunately Champernowne and Cowell do not reproduced the argument, which is the foundation of the derivation of the formula 6. (back)
17. This is called the symmetry property. See p.826 in Microeconomic theory. See furthermore p.94 in Economic inequality and income distribution. (back)
18. See p.106 in Economic inequality and income distribution. (back)
19. See p.99 in Economic inequality and income distribution. (back)
20. On p.106 in Economic inequality and income distribution the scaling effect in μ_Ia is acknowledged. Yet this measure is accepted. Perhaps the reason is, that although variations of the total yield influence the value of μ_Ia(u), they do not affect its ordening of various distributions of u corresponding to their inequality. In other words, when one has μ_Ia(u) > μ_Ia(v) for two utility distributions u and v, then one also has μ_Ia(α×u) > μ_Ia(α×v) for any scalar α. On p.97 the principle of irrelevance of scaling is also mentioned separately, besides the desirable normalization. (back)
21. See p.826 in Microeconomic theory, and p.104 in Economic inequality and income distribution. (back)
22. On p.826 in Microeconomic theory the form of g(u_k) is compared with the form of the utility function U of a risk averse individual. Then the analysis focuses on the expected material yield y = E(x). The expectation y weighs the various possible outcomes x_n with their probability of occurrence. The expected yield y is the analogon of u_k, and the utility function U is the analogon of g. In other words, for risk aversion one has U(y) > E(U(x)). Here U(y) plays the role of g(ν), and the certainty equivalence E(U(x)) plays the role of g(ω). On p.82-83 in Economic inequality and income distribution a similar argument is found. (back)
23. See p.89 in Economic inequality and income distribution. In the used SWF the mentioned problem with the interpretation of u_k occurs. Namely, according to the assumption the SWF prefers a levelled distribution of u_k. However, in a democracy the SWF is determined by the electorat, at least broadly outlined. Therefore one would think, that levelling has already been included in u_k itself. This is to say, an individual k with a large yield u_k would experience a discontent by himself. But this discontent would again reduce his u_k. (back)
24. See p.94-95 in Economic inequality and income distribution for the principle of transfers, and p.97 for the second principle of independence. (back)
25. See p.98 in Economic inequality and income distribution. (back)
26. According to p.98 in Economic inequality and income distribution, then other functions must be used, namely f(u, 0) = Π_k=1^K  u_k and f(u, 1) = Π_k=1^K  u_k^uk. The requirement of a constant total yield is necessary, because f itself is clearly not invariant under scaling. However suppose, that scaling is done with α×u. Then according to the formule 8, f changes into α^θ×f. In other words, this scaling upwards changes the value of f, but not the order of the various utility distributions u. (back)
27. According to the principle of monotony the marginal utility of W must be positive. Now one has ∂W/∂u_k = ∂g/∂u_k = α×θ × u_k^θ-1. Therefore α×θ must be positive. On p.829 in Microeconomic theory the choice α=θ is made. The report Distributionally Weighted Cost-Benefit Analysis by the Centraal Planbureau prefers α=1/θ. In none of these sources the choice is explained. (back)
28. This approach is presented on p.828-829 in Microeconomic theory. (back)
29. This suggestion is done on p.829 in Microeconomic theory. If your columnist calculates correctly, then ω is not a CES function. The elasticity ε_uk of the marginal utility ∂ω/∂u_k equals (u_k^θ / Σ_k=1^K  u_k^θ) − 1. This elasticity clearly does vary with u_k. (back)
30. Let u_m=0. Then one has ω = u_m × (Σ_k=1^K  (u_k/u_m)^θ / K)^1/θ = u_m × (1/K + Σ_k=1,k≠m^K  (u_m/u_k)^-θ / K)^1/θ. Note, that now -θ is positive. Therefore ω=0. (back)
31. See chapter 5 in Economic inequality and income distribution. (back)
32. The curves are calculated with the formula 10. The curves are symmetrical in the perpendicular lines from the three points of the triangle. Since the perpendiculars split the triangle in six smaller triangles, the indifference curves must only be calculated in one of the small triangles (for instance the one with u₁ > u₂ > u₃). (back)
33. Levelling reduces the higher wages, and therefore makes work less attractive. This causes a dead-weight loss DWL. However, at θ=-1 the aversion against inequality is large to such a degree, that the DWL probably is irrelevant. (back)
34. Perhaps once it will become possible to measure the parameter θ empirically by means of large-scale opinion polls among the population. It is interesting to analyze the properties of the Gini coefficient. The coefficient is calculated from G = 1 + 1/K − 2 × (K² × ν)^-1 × Σ_k=1^K (K − k + 1) × u_k for u₁ ≤ u₂ ≤ ... ≤ u_N. See p.142 in Economics of the welfare state (2004, Oxford University Press) by N. Barr. The weighing factor K-k+1 is largest for the lower yields u_k, and decreases in a linear manner for the heigher yields. Note that the weighing factor is determined by the order of all yields u_k, but not by their size. This is a rather crude way to express the aversion against inequality. The value of G corresponds to the size of the area above the Lorenz curve. However, quite different curves can lead to the same area, and therefore to the same G. It is worth mentioning, that according to p.113 in Economic inequality and income distribution G does not satisfy the (second) principle of independence, for measures μ_I of inequality. Your columnist has spent an afternoon in trying to underpin this statement with a numerical example. However, he did not succeed, at least as long as the average yield ν is kept constant. (back)
35. See Playing fair (1994, The MIT Press) by K. Binmore. (back)
36. Perhaps this formula looks abstract. However, it is for instance also presented on p.129 in the book Planning and design of engineering systems (1989, Unwin Hyman Ltd) by G.C. Dandy and R.F. Warner, which is a practical handbook for engineers. Consider the realization of works of infrastructure. Your columnist read this book 21 years ago, when he still was a candidate for a career in water management. (back)
37. On p.832 en 834 in Microeconomic theory it is stated, that the function W(u) represents a social preference. On p.836-837 it is shown, that a welfare function with the form of the formula 12 corresponds to a preference, which is invariant for a change of the origin ξ_k of the individual utility functions u_k. Your columnist believes that this is intuitively clear, because the change of the individual origin ξ_k merely adds a constant to the formula 12. Binmore concludes on p.48 in Playing fair, that the maximin principle of Rawls is not invariant under changes of the origin ξ. On p.837 in Microeconomic theory it is remarked, that an interpersonal comparison becomes impossible, as soon as the preference corresponding to W is also invariant under changes of the parameters α_k. In this case just a single individual k could have an α_k≠0. In other words, W(u) = α_k×u_k, so that k is actually a dictator. Only his interests count. This is a complex matter, which your columnist does not yet understand completely (page 837 is really very far away from page 1). (back)
38. On p.283 in Playing fair Binmore states, that the professional domain of rational ethics would be unthinkable without the interpersonal comparison. (back)
39. On p.88 in Playing fair Binmore calls the selection by means of W_R the proportional solution. He uses the graphical image of a social council, which convenes in order to establish the social contract. The contract regulates the empathical preferences. The council bargains, so that the optimal point σ on the Pareto boundary also must be the solution to the Nash problem. Your columnist plans to shortly devote a separate column to the bargaining problem of Nash. In the Nash problem the point ξ in the figure 5 is the status quo (p.84). The status quo defines the yields of the individuals, in case that their negotiation fails. The coincidence of the solutions of utilitarianism, the maximin principle and the Nash solution forms the core of the model of Binmore - when your columnist understands him well. Binmore elaborates on various related details to such an extent, that this core is somewhat obscured. It is intuitively indeed logical, that the interpersonal comparison α_m/α_n depends on the absolute minima ξ_m and ξ_n, and on the total welfare W_H. The set of possible yields is determined by the national wealth, by the technology, and by possible state interventions. (back)
40. The indifference curves according to the formula 10 could be shown in the figure 5, with K=2. For instance, suppose that θ=-1 holds. Consider an indifference curve, for instance ω=1. Then it dictates the relation u₂ = u₁ / (2×u₂−1). This curve is convex in the area bounded by u₁>¹/₂ en u₂>¹/₂. (back)