Optimization of the growth

First insertion on Heterodox Gazette Sam de Wolff: 26 february 2014

In many columns it has been explained how the Leninist planning agency chooses the optimal growth path, usually by means of intertwined matrices. The western economists commonly prefer to calculate the growth path by means of dynamic one-sector models. The present column describes an optimization model of the Dutch economist Jan Tinbergen, from his book Mathematical models of economic growth. The model is based on a utility function. Tinbergen concludes that such models can not determine the optimal growth, because as yet there is a lack of realistic utility functions.

So far, on this portal the necessity and the possibility of the macro-economic planning are regularly returning themes. The core of planning is formed by the valuation of the present consumption with respect to the future consumption. A technical solution does not exist for this problem, because the solidarity between the generations is essential for this choice. Economics can merely indicate what will be the consequences of the various policy options for the distribution of the consumption across the generations. It tries to keep out the value judgements from its models. The ethics and the morals are external factors for economics, which must preferably be introduced in the models in an abstract and general manner¹.

On this portal the Leninist movement is represented by many texts of the East-German economist Eva Müller. She distinguishes between two types of dynamical models. First, there are the one-sector models, which are used to estimate the growth of the total product. Next, there are the many-sector models or intertwined balances, which can calculate the dynamic growth at the micro-level by means of linear programming.

Often Müller uses linear target functions in order to formulate the policy goals in a mathematical manner. This suggests unjustly, that the social needs can be represented by a sum of money. Müller is aware of this mistake, but she can not invent a better method. As an excuse the reader may consider, that in the early years of the Leninist planned economies the criteria were even more primitive². Other Leninist have proposed non-linear target functions, which taken into account the true preferences of the planning agency. An interesting example of this category is the model of Val'tukh. However, the numerical computations with such improved models are quite complex, and they have never become a common practice.

In the western approach of economics the application of macro-economic, social target functions has never become popular. It is simply too ambitious. The famous Dutch economist Jan Tinbergen gives in his book Mathematical models of economic growth an interesting illustration of the obstacles, which hinder the application of target functions³. The present column repeats his arguments, with occasional supplements and comments. Tinbergen uses a one-sector model, just like Müller, although the linear target function is replaced by a more realistic version.

The assumptions in the optimization model of Tinbergen

The target function of Tinbergen consists of the utility function of the central planning agency. It is obvious that Tinbergen assumes, that the central authority is legitimized by means of the democracy, so that the utility function represents at the same time the collective will of the people⁴. Just like the Russian economist Konstantin Val'tukh or the Czech economist Miroslav Toms, Tinbergen assumes, that the consumption C lies between a minimum value C_min and a saturation value C_max. The consumption is a function C(t) of the time t. Now suppose that the marginal utility of the consumption equals

(1)     ∂U / ∂C = u = ((C_max + C_min − C) / (C − C_min))^ν

Figure 1: Tinbergen Ecu

In the formula 1 ν is a model constant. The function u(C) is chosen in such a way, that she is infinite for C=C_min. For, at this level of consumption the subsistence minimum is reached. The point of saturation, which is defined by u=0, has C = C_max + C_min. Furthermore, note that calculations with the marginal utility imply, that the utility scale is cardinal. This choice can be justified, though she is traditionally disapproved. Tinbergen concludes from the consumptive behaviour of the North-American and French workers, that the constant ν is approximately equal to 0.6 ⁵.

Economists commonly mark down the future incomes by means of a discount factor, a certain percentage, with respect to the present. For, the present income can be used for saving, which yields interest as a future benefit. Tinbergen ignores this discount factor. The consequence is, that in a situation with a growing consumptive level C(t) the future generations can enjoy an ever increasing utility U(t). This may be just, or at least a submission to the course of life. The choice for a certain discount factor would be arbitrary⁶. Eva Müller often uses in her models a time horizon T, which amounts to an abrupt discount factor.

Furthermore, suppose that the size of the population remains constant. Then the number of workers remains constant as well, and therefore the factor labour disappears from the production function. The capital becomes the limiting factor for the production. In imitation of the Domar-Harrod model Tinbergen defines the constant

(2)     κ = K / Y

In the formula 2, Y(t) is the national income, and K(t) is the stock of capital. The constant κ is called the capital coefficient, or in the English literature the capital-to-output ratio.

The national income is expended on the consumption C and stored as savings S. Suppose that the economy develops in equilibrium, so that all savings are invested. That is to say, S = I. Furthermore, note that one has I = ∂K / ∂t. The combination of these two formulas with the formula 2 leads to

(3)     C + κ × ∂Y / ∂t = Y

The determination of the optimal consumption

The model of Tinbergen is interesting, because C(t) can be determined separately by means of the formula 1. Here Tinbergen invents an original argument, which illustrates his excellent economic insight. Namely, the planning agency aims to maximize the total utility of all generations. In formula this is

(4)     find in the presented model the C(τ) that maximizes: Ω = ∫₀^∞ U(C(τ)) dτ

In the formula 4 the symbol ∞ represents positive infinity, so that the interests of all generations are included. According to the formula 4 the planned consumption C(τ) (with τ in the interval [0, ∞]) must be distributed over time in such a manner, that any deviation from the plan would lead to a decreased total utility. Consider for instance the consumption C(t) of the generation at the time t, and split the integral of the formula 4 into two parts

(5)     Ω = ∫₀^t U(C(τ)) dτ + ∫_t^∞ U(C(τ)) dτ

The first integral measures the utility of the consumption for all generations before the generation t. The second integral measures the utility of the consumption for all generations after t. Since the total utility Ω is maximal in the optimal situation, the generation t can not realize a larger Ω with a small shift of the consumption. Thanks to this fact, C(t) can be calculated.

For instance, suppose that the generation t decides to give up one unit of consumption in order to realize extra savings. Then she can invest 1 unit extra, and this enlarges the stock K of capital for the following generations. The formula 2 shows, that thanks to the investment the national income Y of the generation t+1 has increased with an amount 1/κ. Although in the optimum the small shift of 1 consumptive unit does not change the total utility Ω of all generations together, of course the utility of each generation does change. The generation t loses 1 unit of consumption, and that costs a quantity u(C(t))×1 of utility.

When the generation t+1 completely consumes her extra income, then she gains a quantity u(C(t+1)) / κ of utility. Moreover, the extra unit of capital can also be used by all following generations, who thus also receive an additional income of 1/κ. Etcetera. Tinbergen concludes that the total gain of utility for the generations after t has a size of ∫_t^∞ u(C(τ)) dτ/κ. Due to the conservation of Ω the utility loss of the generation t and the utility gain of the following generations must compensate each other⁷:

(6)     u(C(t)) = - ∫_t^∞ u(C(τ)) dτ/κ

The remainder of the argument is simple. Differentiate the formula 6 on both sides with respect to t, and insert ∂u/∂t = (∂u/∂C) × dC/dt. The result is

(7)     κ × ∂u/∂C × dC/dt = - u

Next substitute u of the formula 1 in the formula 7. This leads to an equation for C(t), which has the solution:

(8)     C(t) = C_min + C_max / (1 + B × e^-t/(κ×ν))

In the formula 8, B is obviously an integration constant, which is fixed by the value of C(0). The consumption can never fall below C_min, which acts as a threshold, as it were. It is convenient to equate C_min in the mathemetical formulas to zero, so that henceforth C(t) represents the consumption above the subsistence level. In a similar way Y(t) is henceforth the income above the subsistence level.

The optimal national income

Now that the optimal consumption has been fixed by the formula 8, the corresponding optimal national income can be found by substituting this C(t) into the formula 3. One finds⁸

(9)     Y(t) = - (C_max / κ) × ∫ e^(t−τ)/κ / (1 + B × e^{- τ/(κ×ν)}) dτ

Solving the formula 9 is not simple. It can be done when it is assumed that ν=½, which is indeed a fair approximation of the empirical value of 0.6. With this simplification Tinbergen gets the result⁹

(10)     Y(t) = (C_max / √B) × e^t/κ × arctan(e^-t/κ × √B) + A

In the formula 10 A is an integration constant. Tinbergen wants to determine it by considering the situation t→∞. It is known from mathematics that lim_x→0 arctan(x) / x = 1. Then the formula 10 changes into Y(t→∞) = C_max + A. According to the formula 1 (still with C_min=0) one has u=0 for C=C_max, and therefore this C is the point of saturation of needs. Tinbergen supposes, that finally for t→∞ the national income Y will have grown to such an extent, that the point of saturarion has indeed been reached. In that situation there is no longer any need to save or invest. Therefore one has Y=C_max, with A=0. Now the optimal national income is completely fixed.

Evaluation of the optimization model

Figure 2: Growth of consumption and income
    C_min=1, C_max=4, κ=4, B=16

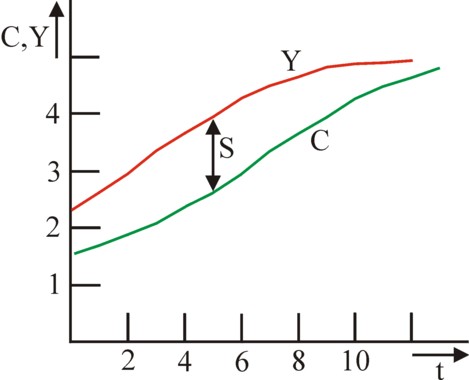
Tinbergen ends with an evaluation of his model. She turns out to be unsatisfactory. Thus Tinbergen concludes that the planning by means of target functions is of little use. His argument starts with the analysis of the relation between the consumption C and the national income Y. Suppose that ∂Y(t)/∂t is approximated by (Y(t) − Y(t-κ)) / κ. When this approximation is inserted into the formula 3, then it follows immediately that one has C(t) = Y(t-κ). That is to say, the consumption is identical to the national income, at the time κ before. The consumption C(t) and the national income Y(t) are shown in the figure 2. The savings S(t) form the vertical distance between these two curves. It is clear that for the optimal consumption the savings at the start must rise, and they must fall again for the distant future.

Interesting is also the exact calculation of the savings S(t). Define the savings quote as σ(t) = S(t) / Y(t). Introduce a temporary variable, namely θ(t) = e^-t/κ × √B (see also the footnotes). Introduce again the threshold C_min in the values C(t) and Y(t). For the sake of convenience define γ = C_max/C_min. Tinbergen derives by means of mathematics that one must have¹⁰

(11)     σ(t) = 1 − (1 + γ / (1 + θ²)) / (1 + γ × arctan(θ) / θ)

Tinbergen has computed numerically, for several values of γ, the maximal possible savings quote σ_max ¹¹. His results are shown in the table 1. The reader sees the problem, that apparently extremely high savings quotes can occur in the optimization model. This is actually caused by the Leninist law of the accelerated growth of the production of the means of production (equipment). That is to say, later generations enjoy an optimal consumption, when the first generations are willing to invest all their incomes.

In the western societies such high savings quotes are never realized. According to Tinbergen the average savings quote in the United States of America and in England is merely about 12% ¹². Apparently the people are simply not willing to make such sacrifices for their (distant) offspring. In the Leninist states, where the planning agency did try, it lead to riots, inspite of the repressive regimes. In other words, the present generation demands that in the formula 4 a discount factor is applied to the utility U(C(τ)).

That discount factor reduces the utility for the future periods, where the national income and the consumption will attain higher values. It is obvious that the discount factor also influences the formula 1. It can not be excluded, that the height of the discount factor can be estimated by asking the people about their preferences. In this way they can express their solidarity with the future generations, which can not yet defend its own interests. But Tinbergen does not want to elaborate on this possibility, and ends his discussion with the conclusion, that economics can not determine the optimal growth. His optimization model is elegant, but for the time being it is merely an academic finger-exercise.

1. Unfortunately the organization theory states that an executive agency will defend its own interests. Weber defines the expert as: someone who knows more and more about less and less, until finally he knows everything about nothing. Therefore the second law of McDonalds does not surprise: consultants are mystical beings who demand a number from an enterprise and subsequently give it back. The observation of Horngren is: among economists the real world is an unrealistic case. In emergency situations there is the first law of Schrank: if something does not work, then make it larger. An interesting application is the law of Matilda about the formation of sub-committees: if you leave the room, you will be in it. Fortunately, there is still hope, also for the laymen. Simply apply the key for success of Ely: create a need and satisfy it. (back)
2. Worth mentioning is the Leninist law of the accelerated (in the German language vorrangige) growth of the production of the means of production (equipment). The law can mainly be found in the older Leninist specialized literature, such as Ökonomische Gesetze im gesellschaftlichen System des Sozialismus (1969, Dietz Verlag) by G. Ebert, G. Koch, F. Matho and H. Milke. In paragraph 3.3 (p.274 and further) it is argued, that the economic growth requires a rapid accumulation of capital goods. The investments obtain a higher priority than the consumption. The authors justify their policy with a reference to several mathematical schemes of Karl Marx. It is obvious that Marx himself would have been shocked by this dogmatic version of his theory, nota bene half a century after its publication. From 1920 onward the Leninist planning agency has during many decades imposed this policy of saving on the people, without asking for permission. In Ökonomische Gesetze the authors finally acknowledge, that this imposed solidarity with future generations is rather unfair, and that, moreover, a saturation of capital occurs. In the Netherlands a similar policy has been implemented immediately after the Second World War, albeit legitimized by the democracy. (back)
3. See p.24 and further in Mathematical models of economic growth (1962, McGraw-Hill Book Company, Ltd.) by J. Tinbergen and H.C. Bos. (back)
4. In the second volume Vaste koers of his trilogy Achter de horizon Willem van Iependaal makes a worker ponder (p.127): That had already become apparent during the demonstration for universal suffrage in The Hague, where the guys of the sailor's union had also been present. The guys of the fleet at the parade for suffrage! There were evidently some rumours, although it did not yet crack. Organized navy people, who besides their gruel and pea-soup demanded the suffrage. The exactingness of the working class did not end! Reduced labour-hours, better education, equality for law, benefits during illness, child protection, arbitrage, invalidity insurance, etcetera. And now the common sailor of the fleet wanted to interfere in the navigation of the ship of state! And the guys on the bridge were already excellent ... (back)
5. See p.25 of Mathematical models of economic growth. Tinbergen uses in his estimation a study of the Swedish economist Ragnar Frisch. Furthermore, Tinbergen estimates that the American consumption is twice the French consumption. He finds as a side result that the French consumption lies 20% above the minimum of subsistence C_min. (back)
6. In the poem De nieuwe roep from the volume De twee vaderlanden A.J. Mussche describes the solidarity between the generations (p.7): Where in former times we shouted and laughed in the busy streets / now I must rapturously and appalled bow for each step of the secret; / in the fainting starry nights in spring / yearning voices rustle, complaining, / which make me shiver, crying with nostalgia, from the mild swoon of my youth. / Is life so much deeper than the youth and the day reveal, / the day of youth, which yet is a dazzling abyss of light around me; / must from the abyss of the nights still the mystery of the stars be clarified, / did I not know the people, my brothers in the former years, / that they now pass me like strangers, in their veil of smiles and tears? (back)
7. The common people are clearly not the target group of this book. Jan Tinbergen misses the social passion and conviction of Sam de Wolff, but as an expert he is a giant. Therefore, your columnist as an autodidact is mighty proud of the present column; who could have guessed this five years ago? He hopes that he truly understands the ideas of Tinbergen, and that they are presented here accurately. The formal mathematics is used again, because the economic comprehension is just emerging. Apparently Tinbergen argues as follows: since the generation t adds one extra unit of capital, all future generation dispose of an extra income of 1/κ. If they completely consume this income, then for each generation t+n the utility rises with u(C(t+n)) / κ (with n=1, ..., ∞). The utility of all those generations rises with Σ_n=1^∞ u(t+n) / κ. In this argument the time until the next generation is always Δt = 1 year. Therefore, the total utility can be rewritten as Σ_n=1^∞ u(t+n) × Δt / κ, and this is precisely the differential form of the integral in the main text, which had to be proven. Here Tinbergen adds, that each generation could evidently save a part of its extra income. In the optimal situation that will naturally not change the total utility Ω, but it does produce shifts between the generations. Your columnist interprets the remark of Tinbergen as follows: suppose that the generation t+n re-invests a small fraction δ of her extra inkomen 1/κ. The generation t+n keeps an extra consumption of (1 − δ) / κ. That yields for all generations after t+n an extra income of δ/κ². The extra utility per generation is u(C(t+n+m)) × δ/κ², with m=1, ..., ∞. A similar argument as before then shows, that one has u(C(t+n)) = - Σ_m=1^∞ u(C(t+n+m)) × Δt/κ. In other words, the formula 6 has indeed a universal validity, irrespective of the investment decisions of each generation. (back)
8. The differential equation for Y(t) is Y − κ × ∂Y/∂t = C(t). Tinbergen states, that one has Y − κ × ∂Y/∂t = - κ × e^t/κ × ∂(Y × e^-t/κ)/∂t. The conclusion is that C(t) = - κ × e^t/κ × ∂(Y × e^-t/κ)/∂t, where now for C(t) the formula 8 can be inserted (obviously again with C_min = 0). Then the integration over t yields the formula 9. (back)
9. For the sake of convenience, Tinbergen introduces the new variabele θ = e^-t/κ × √B. So dθ = - θ × dt / κ. Then the formula 9 changes into Y(t) = (C_max / √B) × e^t/κ × ∫ dθ / (1 + θ²). The integral is known from mathematics, and has the primitive arctan(θ). Next replace θ again by t-functions, so that finally the formula 10 is found. (back)
10. The argument is as follows. According to the formula 8 one has C(t) = C_min + C_max / (1 + θ²). According to the formula 10 one has Y(t) = C_min + C_max × arctan(θ) / θ. It folows that C/Y = (1 + γ / (1 + θ²)) / (1 + γ × arctan(θ) / θ). This leads directly to the formula 11. (back)
11. See p.30 in Mathematical models of economic growth. Incidentally, a ratio γ = C_max/C_min = 10 like in the table is large as well. Such an increase requires many years. A more modest level of ambition would lead to a smaller savings quote, but all right. (back)
12. See p.24 in Mathematical models of economic growth. (back)