
Figure 1: Production possibilities curve
(a) target functions; (b) extra limitations and target function
An essential question in economics concerns the measurement of the utility of a product. The present column describes two approaches, which both attempt to solve this problem. The first one refers to the use value and the target function in the Leninist paradigm. It stems from Miroslav Toms in his book Der Gebrauchswert und seine Messung. The second one refers to the subjective utility function of the neoclassical theory. It is developed by Bernard van Praag in his book Individual welfare functions and consumer behavior.
Since the end of the nineteenth century it has become clear, that the state and the administrations have their own indispensable task in maintaining the economic system. This requires a policy plan, which describes a coherent set of measures, in order to optimize the economic functioning. Loyal readers may remember from a previous column how the economic system can be summarized in a mathematical target function. In another column the objective social needs have been modelled in a mathematical utility function.
The twentieth century is characterized by a, in restrospect, extremely fascinating competition between the Leninist planned economies, the mixed European economies (a capitalist market in combination with a large public sector), and the North-American capitalism. In the Leninism the economic policy is completely fixed by the central administration1. It is assumed that this administration disposes of all relevant information, and she balances the various group interests in the fairest manner. Therefore the policy targets obtain an objective character.
On the other hand, in the North-American system the administration tries to keep a maximal distance with respect to the economy, with the exception of the military sector. Here the economic policy is formed on the private markets, by means of the effective demand. Thus the policy is simply the sum of the needs of the separate households. Apparently, in this case the policy has a subjective character. There is no central policy plan. It can even be said, that such a plan is impossible, because the state is not interested in the social needs, and therefore it does not dispose of the necessary knowledge and information. The European system is a mixture of the Leninist and North-American ones.
It has just been remarked that each of these three system has its own specific demands with regard to the scientific knowledge. Here the Leninism has a high level of ambition, because it attemps to know the objective needs. This ambition is formulated by the fundamental Leninist law: the ultimate policy goal is to satisfy the increasing material and cultural needs of the people better and better, by means of a continuing development and improvement of the social production2. The North-American ambition is formulated well by the economist Lionel Robbins, who defines the economic actions as the human behaviour, as far as it is controlled by the tension between subjective goals, on the one hand, and the relatively scarce and versatile means, on the other hand3.
Both definitions express, that the consumptive needs have to adjust to the limited productive capacity. The difference lies in the referral to the people and the subject (individual), and also in the term social. Those who like to know more about the neoclassical science of capitalism can choose from an enormous supply of economic textbooks. Since the Leninist got the worst of the ideological battle, their knowledge is not so accessible. For the colum, your columnist consults the Leninist book Der Gebrauchswert und seine Messung by Miroslav Toms4. Toms (1944-1988) is a Czech economist, who has tried to connect the theory of Marx and the modern theories.
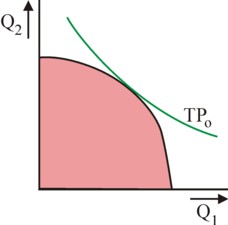
In the book Toms proposes to measure the utility of products, preferably in a quantitative manner. That is useful, because unfortunately a choice must be made regarding the satisfaction of social needs. In the two definitions of the economic actions the problem of the limited production capacity has already been mentioned. For, society disposes of merely an limited quantity of production factors. The quantities of labour and equipment are given. Suppose that i different goods or products exist, with i=1, ..., N, then the possible quantities Qi of products are limited. A choice must be made with regard to the allocation of the production factors to the productive sectors. The figure 1a graphically displays the productive bounds for the case of two possible products. The outer frontier of the possible area for production is called the production possibilities curve.

Suppose that the central planning agency has selected the height of the wage and the depreciation of the equipment. Then the total production costs Tk are fixed. A logical goal of the plan is to maximize the value of the total social product TP. Namely, that would maximize the produced surplus value MW = TP − TK. This requires first of all, to attach a corresponding weight or price pi to each separate product or good i. Next the total product value can be computed as
(1) TP = Σi=1N pi × Qi
The approach is illustrated in the figure 1a. In the case with two products all production possibilities lie in the (Q1, Q2) plane, and the combinations with the same value of TP form a straight line, with as its slope the quantity -p1/p2. The maximization of TP requires that the line is shifted to the right as far as possible. In the optimum the line TPo touches the production possibilities curve. That optimum clearly depends on the price system. Now in the planned economy the problem arises, that the planning agency itself is responsible for the price formation. Each price depends on the objective social utility of the concerned product. It is prescribed at the central level, and not in conformity with the market. It is questionable, whether in this situation the formula 1 can completely guarantee the utility.
For, according to the figure 1a the method leads to a preference for expensive products. That can be undesirable. The planning agency can try to solve this problem by imposing upper boundaries on the production of each good 1, that is to say, Qi ≤ Qimax. Here the reader recognizes the method of the linear programming5. Indeed in the figure 1b a different production optimum is found than in the figure 1a. This is indeed the method, which has commonly been used by the Leninist planning authorities.
Yet Toms proposes a different approach. He replaces the linear TP function of the formula 1 by the linear logarithmic function6
(2) Z = Σi=1N pi × ln(Qi)
In the formula 2 ln() is the natural logarithm. Note, that the formula can be rewritten in the perhaps more appealing form Z' = eZ. That leads to the result
(3) Z' = Πi=1N Qipi
In the formula 3 the mathematical Π symbol represents the multiplication of all N quantities behind it. The formulas 1 and 2 appear to differ notably with regard to the manner, in which for an equal value of the target function Z (or TP) the products 1 and 2 can be exchanged mutually (substituted). The formula 2 leads to the substitution ratio ΔQ2/ΔQ1 = -p1/p2. However, the formula 2 leads to
(4) ΔQ2 / ΔQ1 = -(p1 / p2) × (Q2 / Q1)
What is the effect of the formula 4? Suppose for instance, that the price p1 is much larger than p2. In that situation the formula 1 would command an increased production Q1 of the product 1. However, the formula 4 shows for the Z function of the formula 2, that the price effect is opposed by the term Q2/Q1 on the right-hand side. In other words, in the formula 4 the price ratio determines the relative substitution ΔQi/Qi, instead of the absolute substitution ΔQi. This relation expresses, that the individuals base their utility valuation on the relative differences, so on the ratios, and not on the absolute differences. The reader may recognize this psychological phenomenon from an previous column.
For the sake of completeness the figure 2 shows for the case of two products the indifference (iso-utility) curves for a function of the type Z or Z'. Now the Z curve is not linear, but she has a convex shape. The concave production possibilities curve is also shown. Thanks to the substitution ratio of the formula 4 the optimum consists of a rather well-balanced package of quantities of products.
The maximization of the target function aims to maximize the utility effect of the total social production. The preceding paragraph clearly shows that the price system is crucial for the determination of the productive structure. In Leninism the price formation is done by the planning agency. The prices are computed by means of scientific normatives. This suggests that the prices are objective. They are not the result of subjective market fluctuations. It is obvious that first a method must be developed for the calculation of the normatives. Toms makes some proposals for that end.
In imitation of Karl Marx, Toms uses the concept of the use value. This concept has some similarity with the utility concept of the modern economics, but it must not be equated with it. For, that utility is always attached to the individual or the household. It is subjective. However, the use value is attached to the material product properties or to the social needs. In the first case Toms calls it the individual use value, and in the second case the social use value.
The social use value is included in the social target function of the preceding paragraph. The planning agency fixes the product prices in such a way, that they are an accurate representation of the social demand. The social demand is limited by two extremes. First, there is a minimal demand or need Hmin, which indicates what in the given historical period is the minimum of existence with regard to the concerned product. Second, for each product there will be a quantity Hmax, which finally completely saturates the needs. The degree of saturation or the satisfaction level is defined as
(5) y = (Q − Hmin) / (Hmax − Hmin)
In the formula 5 Q is the supplied quantity of the product. In the situation with Q < Hmin the social use value equals infinity. For, the subsistence minimum is not reached. And in the situation with Q > Hmax the social use value is zero, because the social need is completely saturated. In this respect Toms refers to the model of Val'tukh, which in this manner calculates the total utility effect of the production7. The model of Val'tukh indeed derives the utility effect from the quantities, without using the product prices or other weights. However, due to practical problems this method has never been used on a large scale.
Apparently, the planning agency must attach a value or a degree of saturation to each product. But she can merely do this, when it is obvious which products are most satisfactory for the consumers and users. Precisely for this purpose the Leninism has invented the concept of the individual use value. This value is a normative, which is valued in a scientific manner. In modern economics a similar concept is absent, because this tries to expel norms and values and in general morals from its assumptions8.
The normative depends on the characteristic properties of the concerned product. Each characteristic property k (with k = 1, ..., M) is expressed by a mark ζk. The mark is an indicator of the product. That is to say, each product can be represented by a vector ζ of the corresponding properties. It is obvious that the set of all properties is very large. Think about the physical size, the material, the colour, and the shape. Moreover, each type of product has certain properties, which are attached to its application. For instance, all fuels (oil, coal, wood, gas) have a certain energy content.
Now Toms describes a method, which allows to determine the individual use value of goods, which all are applied for the same purpose. In other words, the products can differ in their material composition, but they are all capable of satisfying the same need. Suppose that a product yields a higher satisfaction with regard to a certain property k, according as his mark ζk is larger. When for the products i and j one has (ζk)i > (ζk)j for otherwise competely equal marks, then the product i has a larger individual use value (or quality) than the product j. The vector ζi will be longer than the vector ζi.
Two products will almost always differ in several marks. In that situation a relative disadvantage in one mark can be compensated by a relative advantage in another mark. Apparently it is now necessary to attach a weighing factor wk to each mark, which determines their relative importance. Besides, it is convenient to choose for each application one of the products from the group as the standard or normal. Suppose that the normal has the marks ζ*. Then each product i in this group can be valued by the composite index9
(6) zi = Σk=1M wk × (ζk)i / ζ*k
In the formula 6 the weighing factors wk are defined in such a way, that they satisfy Σk=1M wk = 1. Thus the composite valuation z* of the normal also equals 1. The obvious question is how the relative weights wk can be determined. In practice this is simply done by forming panels of experts, who each give their expert judgement about the weights. This turns indeed out to yield fairly similar and reliable results. Incidentally, this is also the way, which is employed in tests by present-day consumer organizations. Apparently, humans do apply more or less similar norms.
When for two products i and j one has zi > zj, then the product i has the largest individual use value. However, the reader be warned, that this method does not allow to compare products with different applications. For, the weights are empathically merely valid for a single application. Besides, the z-index does not contain information about the social use value. Namely, when the demand for a product is completely saturated, then the social use value becomes zero, whereas the individual use value maintains a positive value. Apparently the individual use value is independent of the social richness. In more concrete words: someone, who owns a washing machine, will not buy a second one, even when it scores well in a consumer test.
Apparently the individual use value has a limited applicability. Nevertheless it is suited for calculating the utility effect of a product within its own group, for all kinds of product groups. Therefore it can also be estimated, whether the social needs for a product have been satisfied. For, in general the demand will be largest for the product with the highest quality and z-value. Besides, the planning agency will often provide innovative products with a price markup, so that the individual use value can also be expressed in the price formation.
In conclusion of this column it is instructive to compare the previous approaches with the neoclassical utility theory, which is in use nowadays. In this paragraph the utility functions are explained, which have already in 1968 been developed by the economist Bernard van Praag in his thesis10. It has already been remarked, that modern economics studies the subjective utility effects of individuals or households, and not the objective utility effects according to the central policy maker. The utility function of the individual is U(Q), where Q is the vector of product quantities Qi. For the sake of convenience Van Praag considers merely utility functions, which satisfy the condition
(7) U(Q1, ..., QN) = ∫-∞Q1...∫-∞QN u(ψ1, ..., ψN) dψ1 ... dψN
In the formula 7 u(ψ1, ..., ψN) can be interpreted as the composite density function of the probability distribution U(Q). The integral sign in the formula 7 represents an N-fold integration, where the symbol -∞ indicates that each integral begins at a negative infinite value of the integrand. If all values of the upper integration boundaries would be equal to positive infinity (+∞), then one has U(∞, ..., ∞) = 1. The utility function is normalized to 1.
The utility function U(Q) takes into account the complementary properties of the products, and their mutual substitutability. In this sense she is comparable with the social use value of Toms. Therefore also in the function U(Q) phenomena of saturation occur, albeit that those are not complete until Qi→∞, and not already for Qi > Himax. It is interesting that the formula 7 can be integrated to Qj→∞, with the exception of a single product i. Then all needs of the individual are saturated, with the exception of his need for the product i. What remains is the 1-dimensional utility function
(8) Ui(Qi) = U(Qi, ω, ..., ω) = ∫-ωQi ui(ψ) dψ
Van Praag calls Ui(Qi) the partial utility function11. She has a practical meaning. Namely, an individual can never weigh the utility of all N products during his evaluations and decisions. That is impossible for a human being. Therefore in his considerations he will only include those products, which are truly relevant for the decision. In mathematical terms this implies: he reduces the total set of alternative choices to a partial set. It is obvious that he then narrows his view, so that he will miss certain options. For that reason Van Praag calls this behaviour irrationally rational.
The formula 8 is an extreme example of irrational rationality, because the individual merely decides about the quantity Qi, and ignores the substitutions and complementarity. He acts as though the product i is independent of the products j≠i. The formula 8 looks, with regard to its interpretation, like the formula 5 of Toms for the satisfaction level. That is to say, the partial utility function is the subjective analogy of the objective social use value of Toms. Note for the sake of completeness, that in the mentioned model of Val'tukh the social use value does take into account the substitution and complementarity. So it can be done, but Toms prefers simplicity.
It is intriguing that Van Praag also uses a modern analogy or equivalent for the individual use value12. For this purpose he introduces the so-called quality k (with k=1, ..., M), which in fact is similar to the characteristic property of Toms. The quality represents a certain property of the product, and her value is measured by the variable ξk. Van Praag, just like Toms, now divides all existing products in groups, each with a particular application. Within a group the quality of a product i is measured by the so-called welfare measure U(ξi) = U(ξ1,i, ..., ξM,i).
The welfare measure is a special utility function. Namely, she does not compare quantities, but she values each time a single product within its own group. The individual has a specific need or application, and has already decided to satisfy it by the acquisition of a product. He merely has to decide which product. This is also a form of irrational rationality. The welfare function U(ξi) is the subjective equivalent of the zi index of Toms. The difference is that U is normalized on a value interval between 0 and 1. Here it is again assumed, that each quality in the welfare function is saturated for ξk→∞. The U function is a probability distribution, as it where.
Suppose that the qualities k are mutually independent. Then in the same manner as in the formula 8 a partial utility function Uk(ξk) can be constructed for each quality k. The reader sees that Uk(ξk) is the equivalent of the weighed and normalized variable wk × ζk / ζ*k of Toms. The difference is that the value of Uk(ξk) moves between 0 and 1, whereas ζk / ζ*k moves between 0 and ∞. The normalized mark will not necessarily get saturated13.