The fundamental model of the dynamic intertwined balance

First insertion on Heterodoxe Gazet Sam de Wolff: 10 juli 2012

The phenomenon of the economic growth is one of the prominent scientific themes, because it directly influences our prosperity. Economists try to discover the conditions, that contribute to growth. An earlier column shows how the East-German economist Eva Müller expresses the dynamic growth model of Karl Marx in mathematical formulas. That column is followed by a second column, that shows how Sam de Wolff adds the technological progress to the growth model of Marx. The version of De Wolff is able to model the rise in the organic composition in the various economic branches. Both version are very suited for gaining insights into the effects of the economic proportions on the growth. However the presented economic system is rather simple, because they consist of only two (Eva Müller) or three (Sam de Wolff) departments. Besides in the scheme of Marx it is not immediately clear what sums are actually invested in the various branches. Müller must calculate the accumulation quotes separately by using the technical coefficients, and De Wolff uses even more complex methods for the calculation of the accumulation quotes.

In the neoricardian theory the economic system is modelled in an elegant manner by making use of matrix calculations. In its simplest form the model reduces to the open Leontief system, that describes how all product quantities x_i(t) are related to each other. Assume that the system is able to generate at the time t a nett product ψ_i(t) in each branch. That nett product must satisfy the relation

(1)     ψ_i(t) = x_i(t) − Σ_j=1^N χ_ij(t)

In the formula 1 there are N branches, and Σ is the familiar mathematical symbol for summation, in this case over the index j. The symbols χ_ij indicate the quantity of product i, that is needed for the production in the branch j. The set of numbers χ_ij is called the intertwined matrix. Apparently in this context the quantities χ_ij(t) play the role of means of production in all the production processes i. The χ_ij mark the production technique, that is employed by the producer. In case that he would change to another production technique, the intertwined matrix should be modified accordingly. Only if the branch i produces more means of production than is needed in the N branchers, will there be a remaineder in the total nett product.

In the neoricardian theory it turns out to be useful to transform the intertwined matrix into the so-called production coefficients a_ij(t). They are defined by

(2)     a_ij(t) = χ_ij(t) / x_j(t)

Substitution of the formula 2 into the formula 1 yields an interesting result:

(3)     ψ_i(t) = x_i(t) − Σ_j=1^N a_ij(t) × x_j(t)

This formula becomes even more succint, when the vector- and matrix-notation is employed:

(4)     ψ(t) = x(t) − A(t) · x(t) = (I − A(t)) · x(t)

In the formula 4 A is the matrix with as its elements the production coefficients, and I is the unity matrix. Note that contrary to the neoricardian price equations the vector is placed on the right hand side of the matrix A. In other words, here x(t) is a vertical vector.

Formulation of the fundamental model

In the earlier column about the neoricardian theory only a static economic system is studied. Then the economy reproduces itself to all eternity. However, the formula 4 is quite suited for modelling the economic growth. To this purpose a method has been developed, that is called the fundamental model of the dynamic intertwined balance. This column gives an explanation of that model, that is presented by the economist Eva Müller mentioned just now¹. Her presentation can be found in the book Volkswirtschaftlicher Reproduktionsprozeß und dynamische Modelle². The starting point of the fundamental model is, that growth can only occur as long as there are investments in the extension of the means of production. It is assumed that the product technique remains unchanged. This implies that the matrix A is independent of time, that is to say, tne production coefficients are constants. Incidentally Müller calls the a_ij the coefficients of the direct material input (in the German language: Aufwand). Your columnist will follow her in this habit, simply in order to preserve the authenticiy of her argument.

In the study of the economic growth the quantity ψ(t) is especially important. For it contains the wages, as well as the profits and the taxes. These are the factors, that together determine the social prosperity. Then the formula 4 shows, that a growth of ψ(t) must increase also the total social product x(t). For the growth of ψ(t) removes a larger part from x(t), which then is no longer available as means of production. This skimming of x(t) must be compensated by its growth, not as a goal in itself, but just as the means to enlarge the richness. The size of the quantity is determined to a large degree by the fashionable techniques of the production processes. The part A · x(t) of x(t) will be consumed during the production, either as a part of the end product, or as energy or other resources, or as wear of the machinery and buildings. After each production cycle these quantities of products need to be again available in order to start the next cycle. Therefore Müller calls the part A · x(t) the material fund, in imitation of Marx. The term fund expresses that it is a permanent stock of goods³. Incidentally the material fund is also needed in the static neoricardian theory, although in that situation the fund does not expand.

The material fund consists of two components, namely in the terminology of Eva Müller the circulation fund and the basic fund⁴. The circulation fund covers all input of semi-manifactured products and raw materials, that are absolutely necessary for the generation of the end product, and that are partly integrated in it. The main mark of this input is the swift flow out of the production process, say with the completion of the end product. The basic fund guarantees that during the production process the durable means of production remain also available. This is the equipment, like machinery and the factory-buildings, that do not wear in a significant way. Marx calls this the fixed capital. In the case of economic growth, of course the production can only continue, as long as the basic fund expands as well. In other words, not just the circulating material input will increase, but the fund of fixed capital goods as well. In addition the basic fund supplies the means to replace the worn equipment. Incidentally the separation between the various forms of capital (circulation fund, basic fund) can be smooth. For instance oil as fuel is a circulating material input, whereas oil as a brake fluid is a fixed capital good, for in principle durable. And metal can be processed in the end product, but it can also be a durable part in the machinery.

The material fund must be replenished by means of investments i(t) ⁵. Of course they must come from the end product ψ_i(t), just like in the case of the reproduction schemes of Marx. Apparently the following separation of ψ_i(t) is useful

(5)     ψ(t) = i(t) + y(t)

In the formula 5 y(t) is the nett product, that is available for the consumption, with the exception of the investments. Investments can be interpreted as a special type of consumption, namely in behalf of the material fund of capital goods. That is to say, thanks to the investments the fund is built up in the course of time. The wages must be paid from y(t), just like the profits and the taxes⁶. The nett product y(t) is merely consumptive, and is lost for the productive applications (even though of course for the workers the consumption is an existential condition).

Nett investments i(t) occasion a rise of x(t), because at the time t they add production capacity to the material fund. Investments always pertain to a certain time interval, for instance Δt. During this interval the expansion of the total product is x(t+Δt) − x(t). For a time unit this becomes (x(t+Δt) − x(t)) / Δt. One recognizes here the derivative of x(t), expressed as a difference equation. Investments can be made in a continuous manner, or intermittently. If the investments are continuous, then they can be represented by the formula

(6)     i(t) = F · ∂x(t)/∂t

In the formula 6 F is a matrix with as elements the coefficients f_ij of the fund input. The fund input consists of the means of production i, that are present in the fund for the production of the good j ⁷. The elements f_ij are constants, that is to say, they are independent of the time. In fact the formula 6 is a linearization of the increase of x(t) in consequence of the investment i(t). This linearization is justified, because in the case of continuous investments the time interval Δt can be chosen arbitrary small. The formula 6 clearly shows, that a positive investment i(t) is a source term: it forces x(t) to keep growing. Although the formula does not elaborate on the causes of the growth, the preceding text has already drawn attention to the expansion of the material fund (production capacity).

Substitution of the formulas 5 and 6 into the formula 4 yields as result a set of differential equations, that describe the system:

(7)     y(t) = (I − A(t)) · x(t) − F · ∂x(t)/∂t

In comparison with the neoricardian formula 4 the formula 7 contains an extra term for the fund input. Incidentally Eva Müller discusses in her book also two difference equations, in addition to this set of differential equations. In those cases the investment is applied intermittently. The present column is limited to the case of the formula 7 ⁸. This formula completes the analytic modelling of an economy with an expanding production capacity and a nett product. The next step is the solution of the set⁹.

Solution of the fundamental model

The explicit solution of a set of differential equations of the first order requires initial conditions, namely the value x(0) at the time t=0. But it does not suffice for the solution of the formula 7. For this is a set of inhomogeneous equations, and the solution can always be extended with a combination of solutions of the set of homogeneous equations. The set of homogeneous equations belonging to the formula 7 is:

(8)     (I − A(t)) · x(t) − F · ∂x(t)/∂t = 0

First of all the homogeneous solution of the formula 8 is determined. It is immediately clear, that exponential functions satisfy the formula 8, that is to say, functions of the form:

(9)     x(t) = m × e^s×t

In the formula 9 m is a yet unknown vector, that is independent of time. Substitution of the formula 9 into the formula 8 leads to

(10)     (K − I × s) · m = 0

In the formula 10 the matrix K is defined as K = F^-1 · (I − A). The index  ^-1

For convenience the formula 11 is rewritten as a matrix equation. Note here, that m_j can be viewed as a matrix M with elements m_i,j. In addition Müller defines the matrix S, with elements δ_ij × exp(s_j×t). The symbol δ_ij denotes the Kronecker delta, so that S only has non-zero elements on its diagonal. Using these new matrices M and S the formula 11 can be rewritten in the succint form

(12)     x(t) = M · S · c

Now remains the task to find the particular solution for the set of inhomogeneous equations 7. Just now it was remarked that in this formula y(t) is the most interesting quantity. It makes sense to take the following form for y(t):

(13)     y(t) = p × e^r×t

In the formula 13 p is a constant vector, that is to say independent of the time t, that remains to be determined. The quantity r is the rate of growth of the nett product, because one has Δy/Δt = r×y. A planning authority can use the formula 13 in order to prescribe the growth rate, that is desired by her policy. Then the required volume of production x(t) can also be determined. This is exactly the approach, that Eva Müller takes for the fundamental model of the dynamic intertwined balance.

The formula 7 is solved by means of the so-called method of the variation of constants¹⁰. In view of the formula 13 a suited trial solution appears to be

(14)     x(t) = q × e^r×t

The vector q is independent of time and is calculated simply by substitution of the formulas 14 and 13 into the formula 7:

(15)     q(t) = H^-1 · p

In the formula 15 H is the matrix defined by H = I − A − r×F. Thus a particular solution of the formula 7 has been found. Then the general solution of the inhomogeneous set of equations takes the form

(16)     x(t) = M · S · c + q × e^r×t

In fact the formula 16 represents a multitude of solutions, because the constant vector c can take on arbitrary values. The value of c can only be fixed by the initial condition x(0) on t=0. The formula 16 completes the fundamental model of the dynamic intertwined balance.

The construction of the solution in this paragraph is purely mathematical. The reader is warned, that the economic theory puts additional constraints on the method of solution. In any case x(t) and y(t) have to be positive for all times, because they represent quantities¹¹. Also it would be unrealistic to have growth rates s_j in the formulas 11 and 12, that are much larger than the growth rate r of the nett product. The additional requirements place a considerable limit on the number of acceptable mathematical solutions. This means notably, that for the given technique of production, belonging to the matrix A, the investments must be selected with care. That is to say, the choice of the matrix F of the fund input must more or less match A and r. It would be convenient to find the relation between A, r and F in a mathematical way. Unfortunately your columnist does not know how to do this.

An illustrative example

Figure 1: The elements in de matrices A, F, K, S, M and H^-1

As is usual, and in imitation of Eva Müller, the preceding model is illustrated by means of a calculation. The example is again the economic system with two branches, that has been described in the previous column about the neoricardian theory, and that thus is a good acquaintance for the regular reader¹². Of course the difference with the then situation is that now the quantities depend on time. The first branch is agriculture, that is involved in the production of corn (measured in bales). The second branch is the industry, and she produces metal (measured in tons, that is to say, in 1000 kg). Both branches use a part of the produced corn and metal for themselves, as the means of production (in the shape of seed, fuel, equipment, and the like). Of course each branch employs workers. Their wages are paid in bales of corn (for bread, gin etcetera) and in tons of metal (for domestic appliances etcetera). To be precise, the branch of corn uses on a yearly basis χ_gg(t) bales of corn, χ_mg(t) tons of metal, and l_g(t) workers. It produces x_g(t) bales of corn on a yearly basis. Likewise the production factors of the branch of metal on a yearly basis are χ_gm(t) bales of corn, χ_mm(t) tons of metal, and l_m(t) workers, and its production is x_m(t) tons of metal.

In the fundamental model of the dynamic intertwined balance the two differential equations of the formula 7 must be solved. For that some data must be present, first of all the elements of the matrices A and F. If the nett product [y_g(t), y_m(t)] has the form of the formula 13, then in addition p (that is to say, the value [y_g(0), y_m(0)] on t=0) and the growth rate r must be known. And finally the solution of the first order differential equation requires, that the initial condition [x_g(0), x_m(0)] on t=0 is known.

The matrix A is copied simply from the example in the column about the neoricardian theory. For the sake of completeness he is shown again in the figure 1. According to the formula 6 the matrix F determines the volume of investments. The figure 1 shows the values of f_ij, that have been chosen in this example¹³. In imitation of the column about the neoricardian theory, [x_g(0), x_m(0)] = [12, 3.1] is taken as the initial conditions for x. The development of the nett product is determined in an unambigious way by the choice [y_g(0), y_m(0)] = [1, 0.3] ¹⁴ and r=0.1 Then the nett product, and with it the incomes, grow with approximately 10% per unit of time. Thus all data are present for the calculation of the sought development of the total social product x(t).

Figure 2a: The growth curves x_g, (A·x)_g, i_g and y_g in the agriculture

First the general solutions of the two homogeneous differential equations (formula 8) are determined. The solutions have the form of the formula 9. The parameters m and s are determined by means of the method in formula 10. Next the general solutions can be written as in the formula 12, where for the moment the constants [c_g, c_m] remain unknown as yet. In the following text these will be calculated from the initial condition x(0). Here a detailed presentation of the calculations is omitted, and just the results are shown. The figure 1 contains the elements of the matrices K, M and S.

Next the particular solutions of the two inhomogeneous differential equations 7 are determined. This solution has the form of the formula 14. The figure 1 presents the elements of the matrix H^-1. With this also q is known.

The general solutions of the inhomogeneous differential equations are given by the formula 16. Now the constants[c_g, c_m] can be calculated from the initial condition forx(0). The result for the solutions x_g(t) and x_m(t) turns out to be:

(17a)     x_g(t) = 0.3912 × e^-2.802×t + 2.634 × e^0.1764×t + 8.975 × e^0.1×t
(17b)     x_m(t) = -0.5133 × e^-2.802×t + 0.8892 × e^0.1764×t + 2.724 × e^0.1×t

An interesting aspect of the formulas 17a-b is that with the progression of the time t the exponential power with the largest argument will become increasingly dominant. That turns out to be the middle term in the right-hand side of the formulas. Apparently in the long term the total social product obtains a rate of growth of 17.64%. This is larger than the rate of growth r of the nett product y(t), that is fixed at 10% by the central planning agency. Here two remarks can be made. First, apparently the central planning agency believes that the extension of the productive capacity as more important than the consumption. There are huge investments in the expansion of the production of the means of production.

And secondly, apparently in the long term the production in both branches (agriculture and industry) obtain the same rate of growth (17.64%), even though she deviates with respect to the nett product. Then the proportions in the production of the two branches become the ratio of the two middle terms, namely 2.634 / 0.8892 = 2.962 (bales per ton). One may remember, that on t=0 the production started with 12 bales of corn and 3.1 tons of metal, so with a ratio of 3.781. Appartently the proportions of production shift in favour of the industry. In other words, in this economic system the industry is involved in an overtaking manoeuvre, and grows faster than the agriculture.

Figure 2b: The growth curves x_m, (A·x)_m, i_m and y_m in the industry

The formulas 17a-b are not usable for negative times, that is to say, for the historical development of x(t). For then the first term on the right-hand side will dominate the other terms¹⁵. And as one sees from the formula 17b that term leads to negative quantities of x_m(t).

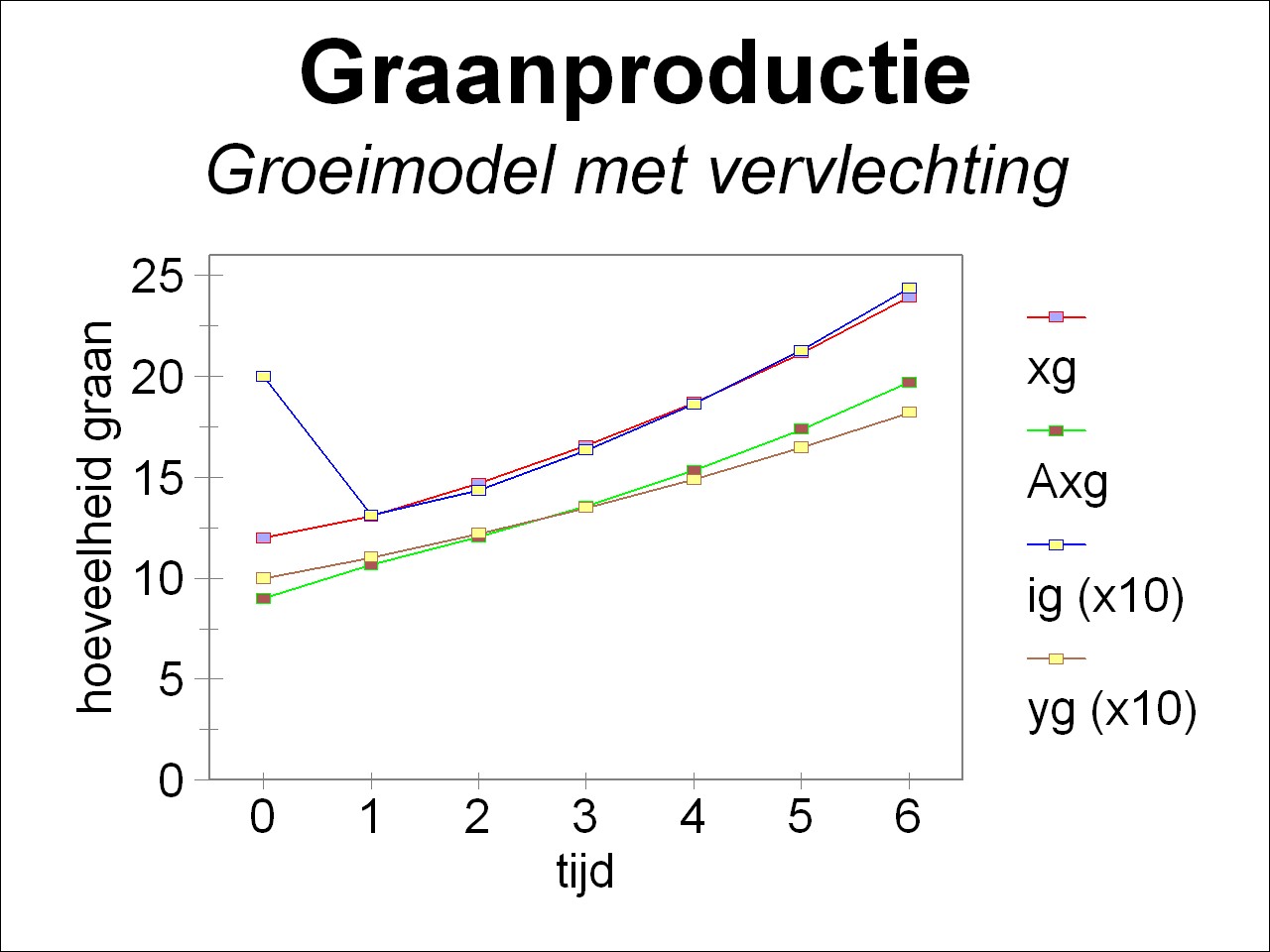
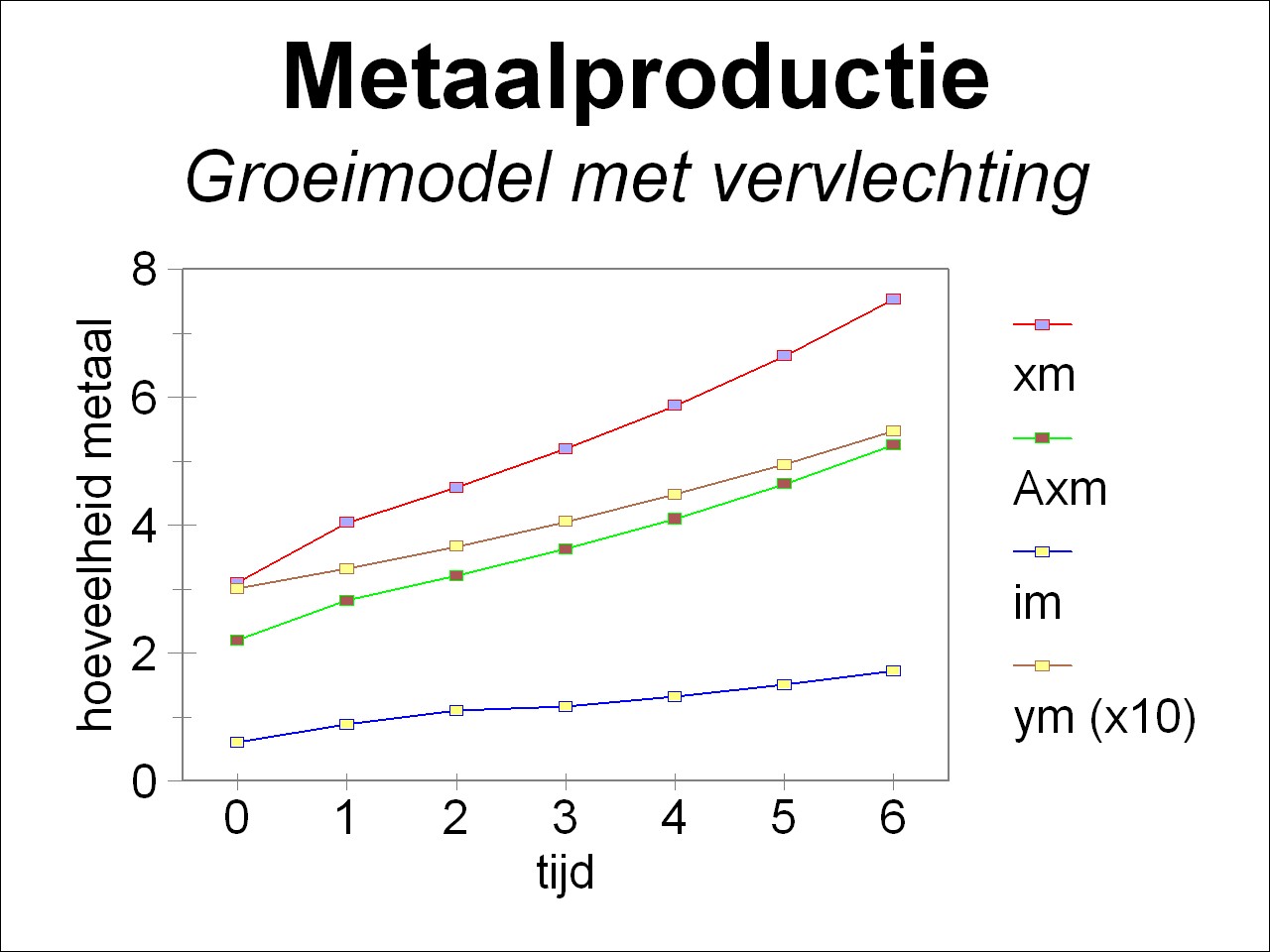
For the sake of completeness the table 1 shows the time development of the total social product (x_g(t), x_m(t)), of the material consumption (A · x(t)), of the investments (F · ∂x/∂t), and of the nett product (y_g(t), y_m(t)). The figure 2a-b shows the time development in an elegant way, for respectively the agriculture and the industry. Clearly visible is how the growth of consumption (the nett product y(t) without the investments) falls behind the productive growth. Of course the central planning agency can at all times decide to choose yet a larger r, if it desires so. It is again remarked, that in these suppositions the technology of production remains unchanged.

1. Eva Müller was employed at the central planning office of the former German Democratic Republic. After that period she remained active in science and in politics for the party PDS, that was the successor of the Leninist SED. She died recently, in april 2011, at the age of 82 Years. (back)
2. See p.277 and further in Volkswirtschaftlicher Reproduktionsprozeß und dynamische Modelle (1973, Verlag Die Wirtschaft). To be fair it must be added that similar models have been developed in the capitalist states, among others by the Dutch economist Jan Tinbergen. A marked difference is that Tinbergen expresses the quantities as money sums. However, in the Leninist economies the prices can be planned at will, so that it is more convenient to use physical quantities. (back)
3. A permanent flow of material does leave the fund, but it is replaced at the same time. (back)
4. Stricktly speaking also the inactive stocks of products belong to the material fund. In this column the stocks are ignored. (back)
5. Again, Müller follows here the convention of Marx to include the expansion of the circulation fund in the investments. This deviates from the western convention to limit the word investment to the expansion of the durable capital goods (basic fund). (back)
6. In the reproduction scheme of Marx this is different, because he includes the advanced wages in the investments. Then the producer must generate a profit from the wage sum, because the sum is a part of the production costs. This is visible in the argument of Sam de Wolff, because he explicitly calculates the accumulation in the wage fund. On the other hand Eva Müller employs in her version of the scheme of Marx a coefficient α, that represents exclusively the accumulation of the means of production. See the pertinent columns. (back)
7. The formula 6 is a special form of the well-known investment equation i(t) = ∂K/∂t. Here K is a measure for the quantity of capital goods (in the model of Müller both circulating and fixed). Note that in case F is independent of time one has F · ∂x/∂t = ∂(F · x) / ∂t. Apparently the vector ∂(F · x) / ∂t represents the fraction of the production x_i, that is added to the stock of capital goods K. Incidentally Müller does not call this the necessary stock of capital goods K, but she uses the expression input of fund (circulation fund and basic fund). Note that the input of already existing basic fund can differ from the input of newly added basic fund (the investments). Therefore the stock of existing basic fund Γ(t) is expressed as G(t) · x, where G is a matrix, that not necessarily equals the basic fund F (although it can). The matrix G(t) has elements g_ij(t) (see p.88 of Müller's book). The quantity Γ_i is defined as Σ_j=1^N g_ij × x_j, and thus adds all inputs of product i as capital goods (basic fund). It seems logical to compare this input of basic fund with the total production x_i. In other words, define the quantity γ_i = Γ_i / x_i. Müller calls γ_i the coefficients of the input of the basic fund in the branch i. Elsewhere, on p.55, she calls this measure the intensity. That is indeed somewhat clearer than the word coefficient, because this manner avoids a confusion of tongues with the coefficients g_ij in the branches. (back)
8. Müller considers the difference equations y(t) = (I − A(t)) · x(t) − F · (x(t+Δt)−x(t)) and y(t) = (I − A(t)) · x(t) − F · (x(t)−x(t-Δt)). In the first case the investment is done only at the end of the interval Δt. In the second case the investment is done immediately at the start of the time interval Δt. In the first case the growth will be slower than in the second case, because the investment is delayed. (back)
9. The method of solution that follows is taken from p.313 and further in Volkswirtschaftlicher Reproduktionsprozeß und dynamische Modelle. The method can also be found in any decent book about mathematical difference equations. (back)
10. The interested reader is referred to any decent book about mathematical differential equations. Thanks to an earlier study in physics your columnist still keeps the book Gewöhnliche Differentialgleichungen (1976, Springer Verlag) of W. Walter in his bookcase. zijn boekenkast staan. There the method is explained on p.23. My teacher at the time referred to the book with the tender name "Waltertje". Your columnist is just as fond of differential equations. (back)
11. In principle x(t) en y(t) can be negative for a short time, as long as stocks can be broken into. However, this kind of nuances do not fit in the present column, that tries to present the growth model as simple as possible. (back)
12. Incidentally it would not be a problem at all for the fundamental model of the dynamic intertwined table to describe a situation with a large number of branches. (back)
13. The choice of F is arbitrary, but she should naturally occasion meaningful economic solutions for x(t). Your columnist has found his F simply by trial and error. Some F matrices must be rejected, because on the long term x(t) would become negative. Besides for certain choices the eigen values s_g and s_m turn out to be complex numbers. Then the general solution of the set of homogeneous differential equations will exhibit an oscillating behaviour, subdued or explosive. Such conjunctural behaviour may be interesting, but it falls outside the scope of the present column. Therefore here a matrix has been chosen that leads to real numbers (also in the mathematical sense) for the exponents, whereby (at least) one is positive. This is the kind of growth, that the central planning agency wants to further. (back)
14. Here the nett product is a third of that in the neoricardian example. For now a part of the neoricardian nett product ψ is expended on investments. Here the numbers are chosen in such a way, that they lead to an elegant solution as the end result. (back)
15. The same phenomenon occurs in the example, that is presented by Eva Müller. See p.316 of Volkswirtschaftlicher Reproduktionsprozeß und dynamische Modelle. (back)