Calculation of business cycles in two branches

First insertion on Heterodox Gazette Sam de Wolff: 23 may 2013

An important question in the research of business cycles is how the market fluctuations, which are naturally inevitable in an imperfect world, are maintained by the economic system itself. In a previous column about the theory of Kalecki it has already been remarked, that indeed the system can under certain circumstances bring itself in a state of oscillation. The present column illustrates this phenomenon by means of an example, which originates from the well-known economists Joan Robinson and John Eatwell. It is a two-sector model.

The example can be found in the popular introductory textbook Inleiding tot de moderne economie¹. It concerns an application of the theory of business cycles according to Michal Kalecki. The example does not add new knowledge, but it does illustrate what the practical consequences are. In particular for the given situation it is shown, that the theory indeed predicts an economic crisis. The assumption of two branches is not typical for the theory of Kalecki, but she does not change the arguments in a significant way. She is especially interesting, since it becomes apparent how in each branch the crisis develops in a different way. Incidentally, the example in the present column uses different numbers than those of Robinson and Eatwell.

The system with two branches

Just like the many preceding columns the present example assumes, that the economic system consists of two branches: the agriculture and the industry. The agriculture produces corn (with the bale as its unit) and the industry generates metal (with the ton as the unit of weight). The agriculture disposes of l_g=20 units of labour time (for instance 20 man years), which produce nett Q_g,N=1.8 bales of corn. The industry disposes of l_m=10 units of labour time. For the moment the system is in a static situation.

The agriculture uses q_gg bales of corn as seeds for sowing, and q_mg tons of metal for tools, which together form her means of production. The metal is obviously supplied by the industry, in such quantities that the worn-out tools can be just replaced. The industry itself employs merely q_mm tons of metal for her means of production, and these tools are produced in her own branch. The table 1 presents the system in the form of a matrix. The rows describe the distribution of the gross product over the branches. The columns describe the production technique of the concerned branch.

The investments I_g of the agriculture require payments to the industry, whereas the investments of the industry are done in her own branch. Note, that this concerns gross investments. The metal is merely replaced, but not extra expanded. The nett investments are zero. In a mathematical form the exchange between the two branches becomes

(1)     I_g = W_m + P_m

Here W_m and P_m are respectively the wage sum and the profit sum in the industry. The formula 1 has been derived first by Karl Marx². She must be immediately elucidated, because in the approach of Robinson and Eatwell the depreciations and the replacements are included in the profit - contrary to the idea of Marx. In the following this aspect will be mentioned again, sometimes in the footnotes. The investment I_g on the left-hand side is a productive demand, which is satisfied by means of the surplus product q_mg = Q_m − q_mm of the industry. The right-hand side describes the costs, which are made by the industry, and the markup for profit as well³.

For the economic system as a whole the income is designated by the symbol Y (without index), just like in the previous column about Kalecki's theory of the business cycles. That is to say, for a given total wage sum W and profit sum P the definition of Y is

(2)     Y = W + P

Since the depreciations are included in the profit P, here Y is the so-called gross added value. The economic system chooses to use corn as its only legal currency. Income consists by definition of corn. Then the nett product Q_m,N of the industry is naturally zero. The wage level is 0.05 bales of corn per unit of labour, so that the wage sums in the agriculture and in the industry are respectively W_g=1 and W_m=0.5 bales of corn.

As usual the profit P_i of branch i (i=p or m) must conform to the general profit rate r of the system. However, the definition of the profit rate differs somewhat from the usual approach, for she is r = P/W. That is to say, the profit P_i is related to the wage sum in the branch, in the form r×W_i. It is evident that both the agriculture and the industry dispose of metal tools, but these capital goods do not yield any rent. They are merely present in the total product, and not in the nett product⁴. It has already been mentioned, that they do exert influence, by means of the replacements.

After fixing the productive sphere of the system in this manner, now the consumption must be modelled. The society has two classes, one for the factor labour and the other for the factor capital. The class of the capitalists is formed by the entrepreneurs themselves. The factor labour expends his complete income on food and other household ware (workers spend what they earn)⁵. Since there is no permanent staff, all labour is productive. Therefore the wage sum is proportional to the gross added value Y_i in the branch (i=g or m), where the constant of proportionality equals the labour productivity ap_i = Y_i / l_i.

The consumption function of the capital owners is

(3)     C_k(t) = C_a + c_k × P(t-θ)

In the formula 3 C_a is the autonomous consumption, which in this example is put equal to zero. The marginal consumption quote c_k is put equal to 0.25, and the time lag θ equals a unit of labour time (for instance a year). The lag expresses the delayed adaptation of the consumption pattern of the capitalist to changes in their income (the profit of the concerned branch). In the present situation, which for the moment is static, the profit does not vary with time.

In the previous column it has been stated that capitalists earn what they spend. Their profit is determined by the amount of investments. The application of the formula 6 in that column, together with the insertion of C_a=0, leads to

(4)     P = I / (1 − c_k)

That is to say, the entrepreneurs invest 75% of their profit. Now the profit rate r can be computed first, and next the seize of the total income Y. The application of the formula 1 leads immediately to r=0.8, or 80%⁶.

Figure 1: Income distribution

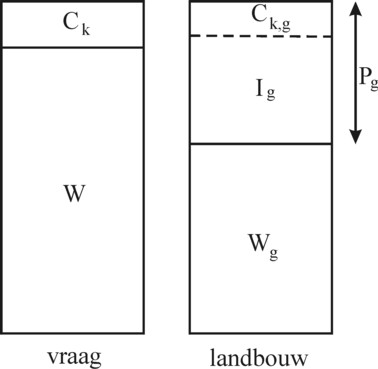
The determination of Y raises the question how the investments I_m of the industry in itself must be computed. This column follows the approach of Robinson and Eatwell in their book. Since that approach is rather cumbersome, and actually does little to increase the insight, your columnist refers for the explanation of their argument to a footnote⁷. There it is shown that one has Y_m=0.9 (measured in bales of corn). The quantity Y_g (the gross added value, or the total income of the branch) is conputed simply from Y_g = (1+r) × W_g = 1.8 bales of corn. The table 2 summarizes all these numbers, and the figure 1 depicts the situation.

Some explanatory remarks with regard to the table 2 and the corresponding figure 1 are in place. First, it is obvious, that the table contains several double counts. A part of the profit sum P_g reappears in the industry in the shape of the wages W_m. But also the profit sum P_m creates extra employment in the industry. Within the industry, profit is converted into wages as well. This has been explained in the footnote. The double count is due to the absence of a time index in the static situation. In fact a part of the profit originates from the investment in wages during the previous time step θ ⁸.

The investment I_g is a demand for tools (metal), which represents a value of 0.6 bales of corn. Here the exchange relation of bales of corn and tons of metal is irrelevant. The same holds for the investment I_m with a value of 0.3 bales of corn. Both investments are paid from the profit sum of the concerned branch. In the footnote it has been explained, that the investment I_m (and thus also the profit P_m) contains a part with a value of 0.1 bales of corn, which is merely required for book-keeping, and which is not really expended.

It can be concluded from the preceding arguments, that the system is a collection of causal relations. They illustrate how investments influence among others the total income⁹. In each branch the profit sum has a size P=r×W. And the investments are I = (1 − c_k) × P. Since according to the formula 2 the total income Y equals W+P, the investments equal Y × (1 − c_k) × r / (1+r). In numbers this is Y = 3×I. This explains once more, now in a different manner, why, due to the sum 0.1 in the book-keeping of I_m, the agriculture must not invest Y_m, as suggested by the formula 1, but merely Y_m − 0.3.

Next consider the following example. Let the economic system be static, but with investments I_g in the agriculture, which are 0.1 larger than in the table 2. How will these two situations differ (this implies a static comparison, not a transition from one situation to the other)? Then the economic structure dictates a larger profit in the agriculture, namely 0.1333. According to the formulas, just mentioned, the total income in the agriculture must be increased with 0.3 bales of corn. And the total income in the industry (the gross added value, including the term for book-keeping) rises by 0.15 bales of corn.

This increase is actually caused by the higher income of the industry, which creates an extra demand in the agriculture. The agriculture must produce more in order to satisfy the demand, but this creates once more an extra demand, namely those of her own extra employed labour and capital. Thanks to the expansion the profit is raised in such a way, that the agriculture can pay for the extra investments (capitalists earn what they spend!).

De conjuncture of the systeem

The previous paragraph may give food for thought, yet it is actually only presented as an introduction for the calculation of the conjuncture in the system with two branches. The approach in the model of Robinson and Eatwell is again used, albeit with adapted numbers¹⁰. Here all aspects of Kalecki's theory of business cycles become visible. First, this requires the assumption, that the agriculture and the industry dispose of a certain reserve in their production capacity. In other words, the utilization of the production factors (including the factor labour) is less than 100%. In a situation, where labour is added, idle tools must naturally be available for that extra labour.

The approach of Robinson and Eatwell models the system by computing all quantities by means of discrete time steps θ. The size of θ can be chosen at will, for instance a man year of labour. Since θ appears in the formula 3, the consumption of the entrepreneurs has a lag of exactly one time step. Contrary to the situation of the previous paragraph, here θ influences the level of consumption during the business cycle.

Robinson and Eatwell choose for the agriculture an investment function of the shape, which has been proposed by Kalecki (see the formula 8 in the previous column). Her formula is

(5)     I_g(t) = I_g(t-θ) − 0.0565 + 0.5 × ΔP_g(t-θ)

The reduction by 0.0565 implies that the entrepreneurs in the agriculture are somewhat more reluctant than in the previous paragraph, and they reduce their investments even for the case of a steady profit P_g ¹¹. According to the formula 5 the entrepreneurs in the agriculture are willing to expand and do nett investments, when the rise of the profit is appreciable. Also here the lag in the behaviour is exactly one time step large.

The calculation of the business cycle starts with the situation in the table 2. The entrepreneurs in the industry invest still their total profit, as far as they do not consume it themselves. In the initial situation (t=0) one has I_g(0) = I_g,a. That is to say, they consist of the autonomous investments, which are just sufficient for the replacement of the worn-out tools. At the time t=0 an external "disturbance" occurs. Namely, the entrepreneurs in the agriculture for once take up a credit at a bank, because they want to do a nett investment. They place an extra order with the industry for tools. In order to execute the order the industry must hire 5 extra units of labour. Then the production capacity of the industry is completely utilized.

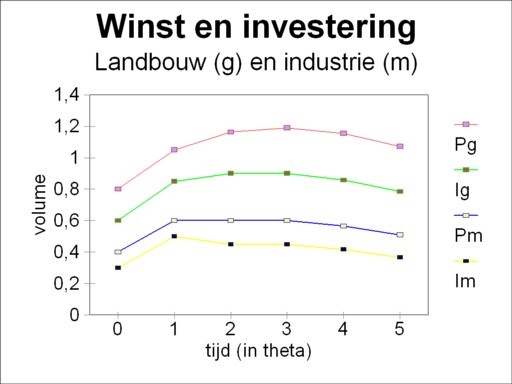
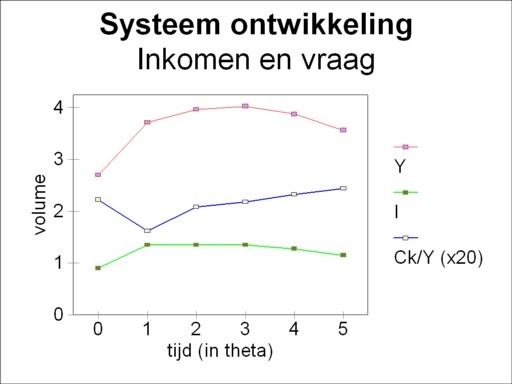
The utilization of the branches is an essential aspect in the study of business cycles. Kalecki points out, that after a full utilization of the capacity the economy can not grow further, at least for the moment¹². She has reached her ceiling. So in the example this phenomenon occurs in the industry. From that moment onwards the development of the system will be followed step-by-step, in intervals with a duration of θ. The computation herself is wisely moved to a footnote¹³. The findings are presented in the table 3. Moreover, the figures 2 and 3 display the developments in respectively the separate branches and the economic system as a whole.

Figure 2: Development of P_g, I_g, P_m and I_m

In the first row (t=0) the numbers from the table 2 reappear. In both branches the wage- and profit-sum maintain a ratio of 1/r = 1.25. In the second row (t=θ) the extra investment ΔI_g = 5 × 0.05, which results form the order by the agriculture, affects the profit sum P_g, and in the industry it affects the wage sum W_m. For the following rows the calculation is straightforward. First, for each t=n×θ the change of the profit ΔP_g((n-1) × θ) is computed. Next I_g(t) is computed from the investment function (formula 5).

Figure 3: Income and demand in the system

The change of the profit at (n-1)×θ yields also the change of the consumption ΔC_k,g(t) of the entrepreneurs in the agriculture. There the change of profit is ΔP_g(t) = ΔC_k,g(t) + ΔI_g(t). And ΔW_g(t) is 1.25 times as large. Furthermore the change of the profit ΔP_m((n-1) × θ) yields the change of the consumption ΔC_k,m(t) of the entrepreneurs in the industry. Next there the wage sum can be computed from ΔI_g(t) = ΔW_m(t) + ΔC_k,m(t). Then the profit P_m(t) and the investment I_m(t) are also known.

The reader will perhaps believe, that the fall continues after t=5×θ. Actually, with this investment function the fall will never stop. But the point has been made, namely that due to the structure of the economic system a crisis can occur by itself, without exogenous causes. And that was the whole purpose of the effort. The figure 3 shows that even a constant investment can already lead the system in a crisis. The quantity C_k/Y illustrates that in the recovery phase the entrepreneurs are less inclined to consume¹⁴. In the fall the consumptive behaviour has a lag, so that the consumptive demand improves, at least in a relative manner. This anti-cyclical behaviour underlies the under-consumption theories.

Several concluding remarks must be made. The implicit assumption is, that the agriculture will not hit the ceiling. As soon as the order at the time t=0 has been completed, the production capacity in the agriculture will be larger than before. It has not been stated, when those extra tools will be delivered. For that is not very relevant. And the question can be raised, whether the example is useful. Robinson and Eatwell believe it does. It may indeed help to see how the crisis develops.

1. See the chapter 6 about the effective demand in Inleiding tot de moderne economie (1977, Uitgeverij Het Spectrum). The English title is An introduction to modern economics. This book is very original, because economics is completely described and explained without making use of the neoclassical paradigm. The book is well written, but it does make demands on the reader - like this column proves. The approach of Robinson and Eatwell underlies also the paragraphs 9.5 and 11.8 of the reader Vooruitgang der economische wetenschap (2011, uitgeverij E. de Bibelude) by E.A. Bakkum. Incidentally, the text in the present column differs slightly from the reader. (back)
2. See for instance the column about the dynamic growth model of Marx. Let the industry be equal to the department I, and the agriculture be equal to the department II. Take in both branches the accumulation quote a equal to zero. Then both branches are static, so that α=0 and G=1. Now the formula 6 in that column implies, that one has K_II = L_I + C_I. Here K represents the investments, L the wage sum and C the profit. The idea of this formula corresponds to the formula 1 in the present column.
   Many feel nostalgic about the vision of Marx. Thus the poet Garmt Stuiveling writes in Tijd en taak (p.73 of the volume Elementen): Like a clarion call the word has sounded: / "Proletarians of all countries, unite!" / Oh wake-up call, oh promise, where still shone / and shine visions, where is now / in these dark postwar years / your strength, your truth now on all sides / proletarians fight proletarians / till within the borders of that same country? (back)
3. The means of production q_mm are produced by the industry herself. This requires an investment I_m of the industry, which she pays from her profit markup. Thanks to the investment I_m the total income Y_m of the industry increases. However, the difference Y_m − I_g is not settled with the agriculture, but it is paid by the industry herself. The sum is used for bookkeeping within the branch. See the following. (back)
4. Usually an efficiency is required for the aggregated capital, which consists of the stock of tools and, in the agriculture, the seeds for sowing. However in this system the means of production are not included in the calculations of the efficiency. Therefore the tools (in case the metal) do not generate income. Due to this assumption the model does not need knowledge about the exchange ratio of metal and corn. And just like Sraffa has shown, then a possible change of the income distribution does not affect the value of the aggregated capital goods. The definition r=P/W of the rate of profit is a bit strange, but on the other hand price formation is always subjective. Thus the definition is not bizarre. Note that r is identical to the marxist rate of surplus value. (back)
5. Therefore Willem van Iependaal in De pionier (p.45 of the volume Op drift) writes an ode for the plougher: He knows the luxury of merely giving: / In the circle of germination there is no perishing! / Again, deeper, the plough-share is driven in / And further, always further the path goes ... / He has not paid attention to his effort: / That which has been ploughed is no longer observed! / He knows: the day has gone too soon ... / Yet a late bird sings in the wood ... (back)
6. The formula 3 states that I_g = (1 − c_k) × r×W_g. The formula 1, wherein I_g also appears, is more difficult to explain. It would seem that one has P_m = r×W_m in the formula 1, but Robinson and Eatwell show on p.134 of Inleiding tot de moderne economie that this is not true. Namely the part (1 − c_k) × r×W_m is invested as I_m in the industry herself. In other words, the income (1 − c_k) × r×W_m creates a demand for metal, and not for corn. The investment I_m is a supply of metal, which is paid by metal. The transaction can be settled on mutual terms, as it where, within the industry herself. She does not create costs. Therefore the term P_m in the formula 1 equals merely c_k × r × W_m. It concerns the nett added value, without replacements. Insertion of the known wage sums gives the result 0.75×r = (1 + c_k×r)/2 = 0.5 + 0.125×r, with as its solution r=0.8. (back)
7. For the calculation of Y the total income Y_m of the industry must be known. Unfortunately it requires some effort to calculate Y_m. In the first instance one has Y_μ1 = W_μ1 + P_μ1. This is the sum, which the agriculture invests and pays to the industry (in bales of corn). It is obvious that the investments of the entrepreneurs in the industry have a size I_m = (1 − c_k) × P_μ1 = (1 − c_k) × r×W_μ1. It is as though the industry has a separate company, where the others can order their tools. Robinson and Eatwell actually include this company in their example. In their approach the separate company does make profit, but it does not invest for itself. Thus the capital owners of the company receive merely their consumption part in corn. Their investment part of the profit is purely virtual and meant for book-keeping. For otherwise the system would expand further. Therefore one has I_m = W_μ2 × (1 + c_k×r), where W_μ2 is the wage sum of the separate company. Apparently the investment creates extra employment in the industry. Combining both expressions for I_m yields the result W_μ2 = W_μ1 × (1 − c_k) × r / (1 + c_k×r). Thus the total employment in the industry implies that W_m = W_μ1 + W_μ2 = W_μ1 × (1+r) / (1 + c_k×r). Insertion of W_m=0.5, r=0.8, and c_k=0.25 yields the result W_μ1 = 0.3333 and W_μ2 = 0.1667. The rest of the industry has twice as much workers as the separate company. However, now a comment must be made with regard to the relation P_m = r×W_m. She is only valid, when the virtual component in the profit is included. For the entrepreneurs of the separate company have in fact given up their profit share (1 − c_k) × P_μ2. That part of the profit is merely present for book-keeping, and not in reality. Therefore one has P_μ1 = 0.2667 and P_μ2 = 0.1333, where P_μ2 contains a virtual part of 0.1 bales of corn. The part for book-keeping contributes the the product value, but it can not be consumed. (back)
8. In a previous column it has been explained how the price of a product is formed by an accumulation of costs, which have been made in the preceding production periods. Precisely because of this phenomenon Eva Müller argues in her book Marxsche Reproduktions-theorie (2005, VSA-Verlag) that in fact the total product should be studied, and not just the added value. The theory of Kalecki does not analyze the productive structure, and that is a limitation. The same critique applies to the work of Keynes. (back)
9. Robinson and Eatwell discuss this extensively in their chapter 6 of Inleiding tot de moderne economie. Here their arguments can be addressed merely in a succinct manner. (back)
10. See the appendix on p.150 of Inleiding tot de moderne economie. (back)
11. See p.152 in Inleiding tot de moderne economie for the investment function of Robinson and Eatwell. The sensitivity for ΔP suggests, that the entrepreneurs in the agriculture react on changes in some marginal profit rate, for instance ΔP/ΔW, or ΔP/ΔK, where ΔK is the change in the stock of capital goods (equipment). The approach clearly has an empirical character. (back)
12. See p.186 in Krise und Prosperität im Kapitalismus (1987, Metropolis-Verlag) by Michal Kalecki. (back)
13. Five time steps are computed, from t=0 to t=5×θ.
    • t = θ: The wage sum in the industry has risen to W_m=0.75 bales of corn. The profit sum must also ris, to P_m=0.6, and the gross added value to Y_m=1.35. But according to the formula 3 the profit part of the industry does not yet create a demand in the agriculture. Only the increased wage sum creates demand. In the end the order results in a nett investment ΔI_g(θ) with a size of 0.25 bales of corn. Now the causal relations come in force. For ΔI_g(θ)=0.25 must be taken from the profit P_g, which therefore must also rise. However due to the lag in the formula 3 the rising profit does not immediately increase the consumption of the entrepreneurs in the agriculture. Thus ΔP_g = ΔI_g(θ). In order to create that growth of profit, the wage sum W_g must grow together with ΔP_g/r = 0.3125 to in total 1.3125. The employment in the agriculture increases.
    • t = 2×θ: the rise in profit of ΔP_g(θ)=0.25 affects the nett investments by means of the investment function I_g(2×θ) (formula 5). However, the industry produces already at its full capacity utilization, so that this extra nett investment can not proceed. The only change is the consumption of the entrepreneurs. According to the formula 3 she becomes 0.15 in the industry and 0.2625 in the agriculture. The wage sum in the agriculture must increase with ΔW_g=0.14, and the employment expands in a corresponding manner.
    • t = 3×θ: according to the formula 5, the rise in profit of ΔP_g(2×θ) = 0.113 will not change the investments I_g(3×θ) in the agriculture. Therefore nothing changes in the industry. The consumption of the entrepreneurs in the agriculture rises with 0.0281 bales of corn. Again the wage sum expands, with ΔW_g = 0.0352.
    • t = 4×θ: the rise in profit of ΔP_g(3×θ) = 0.0281 is so small, that the formula 5 makes shrink the investments to I_g(4×θ) = 0.858. Since for the time being the consumption of the entrepreneurs in the industry remains stable, the wage sum must fall in accordance with ΔI_g, so with -0.0425. The consumption of the entrepreneurs still grows, with 0.007 bales of corn, but due to the shrinking I_g the agriculture is in the end forced to fire workers. Apparently both the agriculture and the industry experience a crisis! In spite of the capacity, which is now available in the industry, there are no new orders.
    • t = 5×θ: the agriculture is confronted with a fall in profit of ΔP_g(4×θ) = -0.035. There the entrepreneurs decrease their consumption and diminish the investments further to 0.784. In the industry the wage sum must also fall, but since at the same time the consumptionC_k,m falls to 0.145, now one has ΔW_m = -0.069.
    (back)
14. See also p.97 and further in The business cycle (1991, Princeton University Press) by H.J. Sherman. (back)