Figure 1: Utility of money
according to v.d. Wijk
An important economic phenomenon is the portfolio of individuals. The portfolio theory studies the form, in which individuals keep their capital. The theory commonly uses the hypothesis of the expected utility of such a portfolio. It turns out, that wealthy individuals tend to display a behaviour of risk aversion. This column reverts to the utility theory of money of Van der Wijk, in order to illustrate the various economic implications of the portfolio theory. Besides the utility theory of money of Van Praag is used to show that individuals can become risk seeking, when the situation is appropriate.
Various columns on this web portal elaborate on the human behaviour, which is observable in all kinds of economic decisions of the individual. That individual bases his judgements on the subjective utility (or in classical terms, which suppose objective preferences: the social use value), which he attaches to the expected consequences. Since the consequences are located in the future, the utility is always a bit uncertain. Decisions are necessarily risky. Sometimes the uncertainties are minimal, for instance for the weekly buy of a fish-and-chips at the local pub. But in general it is worth estimating all risks during the decision-making.
In economics much theory has been developed with regard to the possible consequences due to a decision, notably for the case that those consequences are mutually exclusive. Only one possibility can come true. Such situations require a decision or choice under uncertainty, and the set of consequences of the choice is called a lottery, with a leaning towards drama1. Sometimes the number of results N of the lottery F is finite, for instance rain or not (N=2). Then each outcome has a chance of pn, and a utility un (for instance, rain is good for the harvest). In other cases one has a continuous probability distribution, a probability density f(x), where each outcome x of the lottery has a utility u(x). The present column considers merely lotteries with such a continuous range of outcomes.
The hypothesis (or the theorem) of the expected utility states that the utility can be calculated by means of the formula
(1) U(f) = ∫ u(χ) × f(χ) dχ
The integration runs over all possible outcomes χ. That is a summation, so that here the concept of utility is cardinal. The outcomes χ are located somewhere between -∞ and ∞, where ∞ stands for infinity. U is also called the Von Neumann-Morgenstern expected utility function.
Note, that the cumulative probability distribution F(x) is calculated from F(x) = ∫-∞x f(χ) dχ. For a probability distribution one has F(∞) = 1. For then the sum runs over all possible outcomes. In the same way one has F(-ω) = 0. The integral is written in shorthand notation as F(x) = ∫0F(x) dF. In other words, the density function f(x) is the derivative of F(x). Therefore the expected utility can also be written as U(F).

Figure 1: Utility of money
according to v.d. Wijk
The theory of the expected utility can be explained quite well by means of the theory of the income distribution, which has been developed by Jacob van der Wijk, and which is described in a previous column. Here the "lottery" relates to an individual, who contemplates to migrate to another state. The migration causes certain costs for the individual, and therefore he wants to know whether his future utility of income in his new home will compensate for the costs. Suppose, that he does not know in advance what will be the valuation of his skills. That is to say, in his new situation he will be an average citizen.
According to Van der Wijk the individual utility of an income x is given by
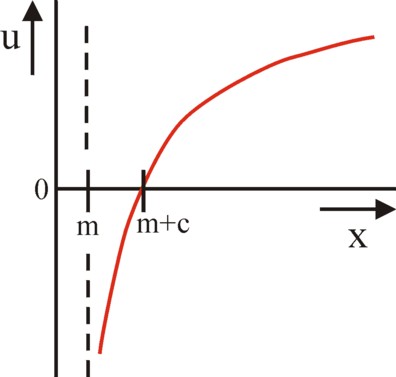
(2) u(x) = ln((x − m) / c)
Here m is the subsistence minimum in the concerned state, and c is an empirical income modulus. Furthermore Van der Wijk assumes, that u is spread in the population according to a normal probability distribution, with an average of zero and a standard deviation of σ². Therefore the income x itself wil be distributed in a log-normal manner.
The figure 1 displays the behaviour of the utility function u(x) in a graphical way. She obeys the mathematical relation ∂u/∂x >0 and ∂²u/∂x² < 0. Apparently her behaviour is concave2. The intuitive explanation is, that the absolute rise of the utility is determined by the relative rise of the income. In other words, the marginal utility of the income falls, when x increases. Even more interesting is that the behaviour of u(x) is characteristic for an individual, who prefers to avoid risks (risk aversion).
First define E(ψ(x)) as the expected value of some function ψ for a given cumulative probability distribution F. For instance then according to the formula 1 one has U(f) = E(u). Another interesting expected value relates to the average income:
(3) E(x) = ∫ χ × f(χ) dχ
An individual is neutral with respect to risk, when his utility function satisfies E(u(x)) = u(E(x)). The following argument proves this relation. He expects that the lottery yields a result E(x), and that gives him a subjective utility u(E(x)). Of course a lottery will seldom yield precisely the expected outcome. The obtained sum can be less than E(x), but also more. Therefore u(x) can be less than u(E(x)), but also more. Furthermore the formula 1 shows that E(u(x)) is his expected subjective utility of the lottery. When these two utilities u(E(x)) and E(u(x)) are equal, then apparently the individual is indifferent with regard to the spread in the truly received x. He accepts the uncertainty. On the other hand, when U(f) = E(u) < u(E(x)), then the individual has a leaning towards risk aversion. And when U(f) = E(u) > u(E(x)), then he is risk seeking3.
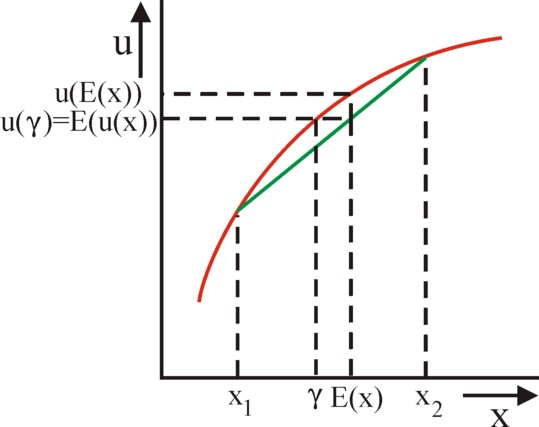
Figure 2: E(x) and γ with risk aversion
The argument makes plausible, that a risk-neutral individual is characterized by u(x) = α × x + β, where α and β are constants. The utility of money is linear in x. On the other hand the figure 2 displays the utility for an individual with risk aversion, such as presented by for instance Van der Wijk. The argument in the common theory is as follows. Suppose for convenience, that the probability distribution F has only two outcomes, namely x1 with a chance p1, and x2 with a chance p2 = 1 − p1. Then one has4
(4) (E(u(x)) − u(x1)) / (E(x) − x1) = (u(x2) − u(x1)) / (x2 − x1)
According to the formula 4 the point (E(x), E(u(x))) is located exactly on the line piece between (x1, u(x1)) and (x2, u(x2)). The figure 2 shows clearly, that an individual according to Van der Wijk, with a concave utility function, values u(E(x)) higher than the expected utility U(f) = E(u(x)). The individual avoids risk, because he prefers the monetary sum E(x) above a lottery, which has that sum as the expected outcome. Thus the figure 2 illustrates, that the utility of the lottery equals a monetary sum γ, which is less than E(x). The sum γ is called the certainty equivalent of F, and it satisfies u(γ) = U(f). The individual is willing to participate in the lottery, when he must pay a fee γ.
Now consider again the case of the individual, who plans to migrate to another state. In this case one has E(u) = U(f) = 05. The formula 2 shows, that this requirement is satisfied for a certainty equivalent of γ = m + c. It is also possible to compute E(x)6, and the result is E(x) = m + c × exp(½ × σ4). The power of e exp(½ × σ4) is larger than 1, so that indeed one has γ < E(x), in agreement with the conclusions in the previous paragraphs. A concrete example of Van der Wijk7 for the Dutch incomes in the tax year 1915-1916: he computes empirical values of m = 568 guilders, c = 49.84 guilders, and σ² = 0.8024. It follows that γ = 618 guilders and E(x) = 637 guilders.
An increasing value of the variance σ² implies, that the spread of the utilities in the population increases. That introduces an additional uncertainty for the future utility of the migrant. Therefore an increasing spread also enlarges the difference between E(x) and the certainty equivalent γ 8. The migrant will demand a higher average yield in return for the sum γ, which he invests in the lottery.
In the economic theory two measures are used to establish the behaviour of risk aversion. The Arrow-Pratt coefficient of absolute risk aversion is defined by r(x) = − ∂²u/∂x² / ∂u/∂x. A higher value of r(x) implies, that the individual is very risk avoiding. In the case of the utility function of the formula 2 it equals r(x) = 1 / (x − m). This function falls for an increasing x. Apparently the individuals are willing to accept a higher risk, according as their wealth increases.
The second measure is the coefficient of relative risk aversion. It is defined as ρ(x) = x × r(x). In the model of Van der Wijk, which includes an existence minimum m, a more logical definition may be ρ = (x − m) × r. Thus in that case the coefficient ρ obtains the value 1. In other words, the coefficient ρ is more critical than the coefficient r. For a decreasing absolute risk aversion does not necessarily imply a decreasing relative risk aversion.
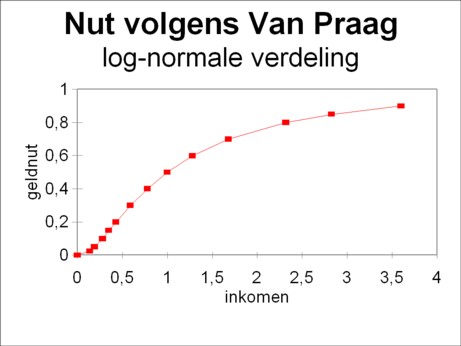
Figure 3: Utility of money according to Van Praag
The assumption of risk aversion is logical, but in certain circumstances she can be wrong. For sometimes the individual will be risk seeking. In the previous column about the cardinality of the marginal utility the theory of monetary utility according to Bernard van Praag has already been explained. There it turns out, that individuals attach little utility to a very low income, because it simply serves no purpose. For instance, one can not live on one potato per day. And merely a left shoe is useless. The income x becomes useful, as soon as a certain minimal threshold is exceeded. In fact Van der Wijk draws the same conclusion, when he introduces the subsistence minimum m.
In the mentioned column it is explained, that according to Van Praag the marginal utility of the income x is given by the normal density function fN(y), with y = ln(x). Therefore the utility u(x) of the income equals the cumulative log-normal probability distribution. This distribution, which runs from 0 till 1, is displayed in a graphical manner in the figure 3. For the sake of convenience, here σ² is equated to 1. The figure shows clearly, that for low values of the income x the utility function is convex and not concave. That corresponds to a risk seeking behaviour. The individual is willing to accept risky lotteries, so that the fee is larger than the expected outcome. In this range of incomes the coefficients of risk aversion are negative.
The portfolio theory describes how the individuals (or households) invest their richness in various types of assets, which together form the investment portfolio9. This subject seems to differ from the theme in the preceding paragraphs, which discuss the incomes. But for instance Van der Wijk uses the formula 2 for the utility also for richness, albeit with different values for the constants m and c. Each type of asset in the portfolio has its own probability distribution of profits or rents. Therefore the type of asset can be interpreted as a lottery. Then the portfolio itself is obviously also a lottery. In this situation the individual must choose the portfolio, which yields the highest utility for him.
The aggregated richness of the individual is given by the formula
(5) V = K + D + G + M
The right-hand side of the equation in the formula 4 consists of four types of assets. Here K represents the credits to enterprises, including shares, D represents the deposits (savings) with banks, and M represents the money in cash (liquidity). The type G represents capital goods, which are purely physical10. Think about land, real estate, art, jewelry, etcetera, in short, rather scarce goods.

Figure 4: Valuation rate for money
Each type of asset has its own qualities. The money M is liquid and not subjected to changes in value, with the exception of inflation. Therefore the possession of money gives security. This is expressed in the psychical valuation rate IM (in the German language: nichtpekuniäre Verwertungs-rate), which is rather large for cash. This advantage of money is called the liquidity premium. The assumption is, that the psychical valuation rate falls somewhat, according as more of the concerned type of asset is possessed. The falling tendency is illustrated in the figure 4.
The behaviour in the figure 4 reminds naturally of the falling marginal utility, but IG must not be interpreted as a (marginal) utility. She is a psychical gain of richness. Note that keeping cash does not yield any financial profit. This also holds for the type of asset G, perhaps with the exception of land and real estate, which sometimes produce a rent. Besides G is less liquid than M, and its value is always subject to speculation. These uncertainties affect the height of the psychical valuation rate IG of the capital goods. However, contrary to the type M, the type G has the advantage that it is not subject to inflation.
On the other hand, the keeping of a deposit at a bank does produce a financial profit on capital, say with a size of iD. Thus the total valuation rate of deposits is equal to ID+iD, where ID represents the psychical component (the degree of certainty). Also the credits to enterprises yield a financial interest, say iK. Then the valuation rate for the type K is IK+iK. Since credits to enterprises are riskier than bank deposits, for the same invested sum IK will usually be less than ID. In principle both types K and D are subject to inflation, but not the value of stocks.
Just like the consumer tries to balance the marginal utilities of all his consumer goods, so the investor will try to balance the valuation rates of the various types of asset. The equilibrium relation is
(6) iV = IK + iK = ID + iD = IG = IM
In the formula 6 the inflation is neglected. Note that IG, ID and IK are a priori valuation rates. They represent the feeling of the individual, and not the final (a posteriori) real outcome of the concerned type of asset.
The psychical valuation rates IG, ID and IK have a falling tendency for an increasing richness, similar to the form of IM in the figure 4. The reason is that the investor will feel less secure, according as a larger part of his total richness V is tied up in a single type of asset. In other words, a diversified portfolio offers more certainty than a homogeneous one. A setback in the valuation rate of one type of asset can be compensated by a windfall in the other.
Moreover it has been explained, that each type of asset has its own specific qualities, so that also therefore it is desirable to adapt the composition of the portfolio. Thanks to some shifts between types the attraction of the portfolio as a lottery can be increased. The formula 6 shows, that the enterprises can influence the decisions of the investors by increasing their interest rate iK. For then IK can have a lower value, so that more K can be invested. In the same way the banks can influence the decision of the depositors by increasing their interest rate iD.
Now consider the behaviour of risk aversion in the composition of a portfolio11. Suppose that the individual can choose merely between the types of asset K and M. When again the inflation is neglected, then the cash maintains simply its value. The expectation E(M) equals M. The expectation E(K) is more difficult to determine. Even when iK is known in advance, and is positive, then the value of the investment can fall unexpectedly, for instance in the case of shares. Moreover the enterprise could go bankrupt. Thus the true profit rate ι of K is uncertain12. The yield κ = ι×K is determined by the cumulative probability distribution F(ι). Therefore E(K) equals K × E(ι) = K × ∫ ι dF(ι). Obviously one has E(ι) = E(K) / K > E(M) / M = 1, because only then a risk avoiding individual will invest in the uncertain type K.
Together the richness V of the individual will generate a future yield κ + M. The utility maximization problem of the individual has the form
(7a) maxK,M ∫ u(ι×K + M) dF(ι)
(7b) onder de voorwaarde V = K + M
Note that for a given richness V here actually a single quantity must be maximized, namely K/V, the fraction of the credits to enterprises in the total richness V. For M/V = 1 − K/V. It can be shown by means of mathematics, that the solution K=0 can never be optimal13. This illustrates the general principle, that an individual with risk aversion will always invest some richness in K, as long as the risk of K yields a profit (that is to say, E(ι) > 1). He will never keep al his richness as cash!
Finally note, that also the formula 6 is the result of a personal optimization process, Therefore there must exist a relation between on the one hand the valuation rates IM and iK+IK, and on the other hand the distribution function F(ι) and the utility function u. Unfortunately at the moment your columnist is not able to formulate that relation14.