The transformation problem in the theory of Marx
First insertion on Heterodoxe Gazet Sam de Wolff: 18 june 2012
E.A. Bakkum is professionally active in the Sociaal Consultatiekantoor, where he holds the position of solicitor. He loves to reflect on the labour movement.
The price theory of Marx
In this column an exposition is given of the so-called transformation problem in the theory of Karl H. Marx1. This problem deserves attention, because it has been used by adversaries of Marx to discredit the marxian theory. The first criticism of the transformation was already passed in 1907 by the economist L. von Bortkiewicz. In the sixties this criticism has been formulated in a more clear and understandable way by P. Sraffa and his followers. The marxist theoreticians did succeed in refuting the criticism of von Bortkiewicz and Sraffa, but this did not yet rehabilitate the theory of Marx. It remained unclear, what Marx tries to say. Only recently, in 2007, did the economist A. Kliman publish an explanation of the theory of Marx, that restores the logic in its entirety2.
The debate is provoked by the manner, with which Marx calculates the prices of products. This column assumes that the reader is already familiar with the marxist theory. Therefore the present paragraph contents itself with a short and compact reproduction of that theory, merely to define the various quantities. If desired the ignorant reader can inform himself in one of the many introductory books3, or perform a search on the world-wide-web. Marx is convinced that at the fundamental level the product value is determined by the amount of labour time expended in its production. Indeed this sounds plausible. However it should be realized, that the labour theory of value is just an abstraction of the real world. According to Marx the total national product, that is to say the sum of all goods produced in the state, has a value C', which can be divided into three components
(1) C' = c + v + m
Incidentally, the formula 1 is also valid for each separate product, and for the total production within an economic branch. In this sense she has a universal validity. In the formula c represents the value of the used means of production (expressed in the labour time, that was needed for the production of those means of production), and v is the value of the package of goods, that the personnel receives in exchange for their working on the product C'. The components c and v are called the constant and variable capital, respectively. The component m is typical for the capitalism, and is called the surplus value. This is the value (of course also expressed in labour time), that the workers add to the product C' without receiving a compensation. The producers appropriate the surplus value m for themselves, and thus realize an income for themselves. In the price system, such als is visible in the actual society in which we live, m is equal to the total profit π.
Marx is an artist in the use of language, and he calls this appropriation of m by the producers an exploitation of the workers. Incidentally in his time, when the inequality in wealth was still poignant, this was a fairly accurate description. Then he defines the ratio m/v as a measure of exploitation. He calls it the degree of exploitation, or sometimes in a more neutral tone, the rate of surplus value, and he represents it by the symbol m'. Marx assumes that the workers can estimate in a reasonably accurate manner how large the degree of exploitation m'i in their own enterprise i actually is. For a high degree of exploitation means, that the workers in the enterprise must make relatively long working days in order to produce the large profits of their employer. The workers will resent to remain into service of such an extreme employer. Therefore according to Marx the rate of surplus value m' is nearly equal for all producers. A general average rate of surplus value is prevalent in the system.
Now Marx makes it his task to determine the general profit rate r*. The profit rate is defined as the profit (here m), divided by the capital invested in the production. Obviously the means of production c are a part of the investment sum4. Since Marx assumes that the wages are paid at the start of the production process, in stead of afterwards, also the wage sum v must be advanced. Thus the production costs C, the invested capital, has a size c+v:
(2) C = c + v
And with this the general profit rate is also known:
(3) r* = m / C
Note that thus the formula 1 can be rewritten into C' = C × (1+r*). However the effect of the formula 3 on the prices of the different products is more interesting. Suppose that the producer i produces a quantity Qi of goods, and in the process makes costs Ci = ci+vi. He wants to realize the general profit rate r* on his advanced capital, and therefore must price each unit of product according to
(4) pi = (ci + vi) × (1 + r*) / Qi
The formula 4 is the so-called price transformation, that Marx uses to calculate the product prices from the product values (in labour time). The transformation formula takes into consideration, that the invested capital must yield a general average profit rate r* on the capital market. If this would not be the case in a certain branch, and for instance the profit rate would be below the average, then the capital would leave this branch. In other words, the competition on the capital market forces all production to yield the same general average profit rate.
The price formula 4 has a curious consequence. According to the formula 1 the producer i generates an amount of products Qi with a total labour value of Ci+mi. On the other hand, the formula 4 states that his nominal yield of money is equal to Ci + r*×Ci. Can the labour value of Qi coincide with the price sum? That is to say, is mi = r*×Ci possible? Is the general average profit rate already valid on the level of the individual producer? The definition of the rate of surplus value leads to the relation mi = r*×Ci. Apparently the produced surplus value depends only on the hired quantity of labour vi (because m' is a social given), and not on ci. Therefore there is no reason, that the surplus value mi of the individual producer i should match r*×Ci. At the level of the separate company i this will mostly not be the case.
Apparently it can be concluded from the price transformation 4, that the value production and the monetary yield are separated at the level of the individual producer. Some producers will make more profit than they generate as actual surplus value, and other will make less profit. Producers that hire a relatively large amount of labour, produce a relatively high surplus value, and will have to transfer a part to others. And producers that prefer to automate, and thus do not hire much labour, produce a surplus value below average. They will receive a compensation. The existence of the general average profit rate on the capital markets leads to a redistribution of the total social surplus value. Of course the redistribution is not a conscious process, but it happens as it were behind the backs of the producers, simply because they do their calculations in prices and not in labour values. Marx assumes that the redistribution does not reduce the labour value in the society as a whole. That is to say, after the redistribution the value of the total product C' and the profit m remain unaffected.
Marx defines as a measure for the labour intensity in a company (or branch) the quantity ci/vi. He calls it the organic composition of the capital, and usually represents it by the symbol oi. Thus the invested capital is given by Ci = vi × (oi + 1). The quantity oi varies, depending on the producer, and especially on the branch. For instance, public utilities with their expensive transport networks, have a higher organic composition than the commercial trade. According as oi of the producer is higher, he will receive more additional surplus value. This becomes clear, when the formula 3 is applied for the calculation of the profit rates in the branches:
(5) r*i = m'i / (1 + oi)
Since m' is determined by the society, one finds m'i=m', and a different oi has the automatic implication of a different r*i. If oi is above average, then the profit rate in the branch i is too low, and it will be compensated by means of a redistribution of the surplus value until the level of the general average profit rate is reached.
Qualitative descriptions of the transformation problem
It has just been said, that in 1907 the first critique is published with regard to the price transformation of Marx, like it is shown in the formula 4. However the arguments of the critics did not yet excel in clarity. A more convincing exposition of the transformation problem is given in 1976, by W. van Drimmelen5. Van Drimmelen believes that Marx makes a mistake by calculating the general average profit rate by means of the labour values m and C. For the producer does not know the labour values, and fixes his product price on the basis of money prices. In other words, he calculates his product price by means of the profit rate r, which the capital market dictates for the efficiency of its lent capital sums6. If the price sum of the production costs, namely the advanced money capital for the means of production and for the workers, is represented by Γ, then one finds r=π/Γ. Apparently the arithmatic method of Marx is only meaningful as long as the profit rate in labour values r* is equal to the profit rate in money prices (that is to say, r*=r). Marx believes that this is the case, for he assumes (like already has been remarked) that on the social (macro-economic) level all labour values remain conserved and thus m=π and C=Γ. Van Drimmelen shows that in general this will not be true. To that end he construes an example, that displays the absurdity.
Suppose that the producers together spend their entire monetary profit π and thus their surplus value m, on luxury goods. These are goods, that bring pleasure, without adding to the production process. Suppose in addition that the organic composition in the branch of luxury goods is very low. In the preceding paragraph it is explained, that a mechanism of redistribution will be started. In the exchange on the markets the branch of luxury goods can not claim its generated surplus value in its entirety, but it is forced to hand over a part of its money claim to the other branches. Thus the price sum of the luxury goods falls below its labour value. The luxury goods are not sold with a profit m, but with a smaller profit π. In the example of Van Drimmelen the other (remaining) branches in this economy produce the means of production and the wage goods. The value sum of their total product is C, and the price sum is Γ. Since the example assumes that these branches have a higher organic composition than the branche of the luxury goods, the mechanism of redistribution will raise the price sum Γ above the value C. Apparently the equality of the price sums and the value sums (π=m, Γ=C) is violated. In other words, the monetary profit rate r would differ from the profit rate r* in labour values. The find of Van Drimmelen is original, as far as it shows in a clear way the role of the organic composition in the transformation problem.
The economist E. Feess-Dörr illustrates in a slightly different way the transformation problem7. He abandons the idea of the luxury branch, and considers an economic system with two "departments"8. Suppose that the physical composition of the package of products, that respresents the surplus value m, is different from the composition of the package of products, that represents the advanced capital C. This is for instance the case, when the economy does not grow, so that the means of production and the army of workers are not expanded. In that case the producers will be forced to consume their entire surplus value. In other words, the surplus value is generated only by the department (branches) that produce consumption goods. On the other hand the advanced capital C also contains all kinds of means of production. In general there is no reason why the organic composition for the production of the consumption goods should be equal to the organic composition for the production of the means of production. Also here the surplus value of the producers must be redistributed in order to guarantee the general average profit rate. Again the equality of the monetary profit π and the surplus value m would be destroyed. The profit rate r* in labour values would differ from the profit rate r in price sums. Of course the argument of Feess-Dörr is principally the samen as that of Van Drimmelen.
A quantitative description of the transformation problem
An example may help to illustrate the effect and the impact of the transformation problem. In particular it gives an impression of the deviations of the marxist prices with respect to the real prices. The real prices can be calculated with the theory of Sraffa, which has already been introduced in a previous column. In the theory of Sraffa the calculations can be performed without dubious assumptions like π=m and Γ=C. There, in that previous column, an example is used, that will be copied in the present column9. The economic system consists of two branches, namely the agriculture (index g) and the industry (index m). The agriculture produces corn (expressed in bales) and the industry produces metal (expressed in tons of weight). Table 1 gives a survey of the quantities. For the explanation of the symbols in the table 1 the reader is invited to just consult the previous column. This is advisable anyway, because in the following also the numerical results of that column will be used.
Table 1: core variables of an economic system consisting of agriculture and industry
Source: paragraph 6.1 in Vooruitgang der economische wetenschap
| agriculture | industry | nett product |
|---|
| corn | qgg=5 | qgm=4 | Qg,N=3 |
| metal | qmg=0.2 | qmm=2 | Qm,N=0.9 |
| workers | lg=20 | lm=10 | |
| production | Qg=12 | Qm=3.1 | |
According to the theory of Marx the labour values form the foundation for the calculation of prices. The labour values must obey the formula 1, both at the level of the company, of the branch or department, and of the whole society. In order to rewrite this formula use is made of the relation
(6) l = v + m
The formula 6 simply states that the total amount of labour l expended on the product is equal to the sum of the wage v and the surplus value m. After substitution of the formula 6 the formula 1 is expressed as C' = c + l. For the present case with two branches this formula implies that10
(7a) ηg×Qg = ηg×qgg + ηm×qmg + lg
(7b) ηm×Qm = ηg×qgm + ηm×qmm + lm
In the set 7a-b ηg is the labour value of a bale of corn, and ηm is the labour value of a ton of metal. In the previous column about the theory of Sraffa it is explained that it is preferable to eliminate the aggregate quantities Qg and Qm by means of a division. Then a set of technical coefficients is left, that depend exclusively on the applied technology. Table 2 summarizes the values of the technical coefficients, such as correspond to the table 1.
Table 2: technical coefficients
Source: paragraph 6.1 idem
| agriculture | industry |
|---|
| corn | agg=0.4167 | agm=1.290 |
| metal | amg=0.01667 | amm=0.6452 |
| workers | ag=1.667 | am=3.226 |
The production coefficients can be expressed as a matrix A, and the labour coefficients can be expressed as a (horizontal) vector a. Then in the matrix notation the set 7 of coefficients takes the form
(8) η = η · A + a
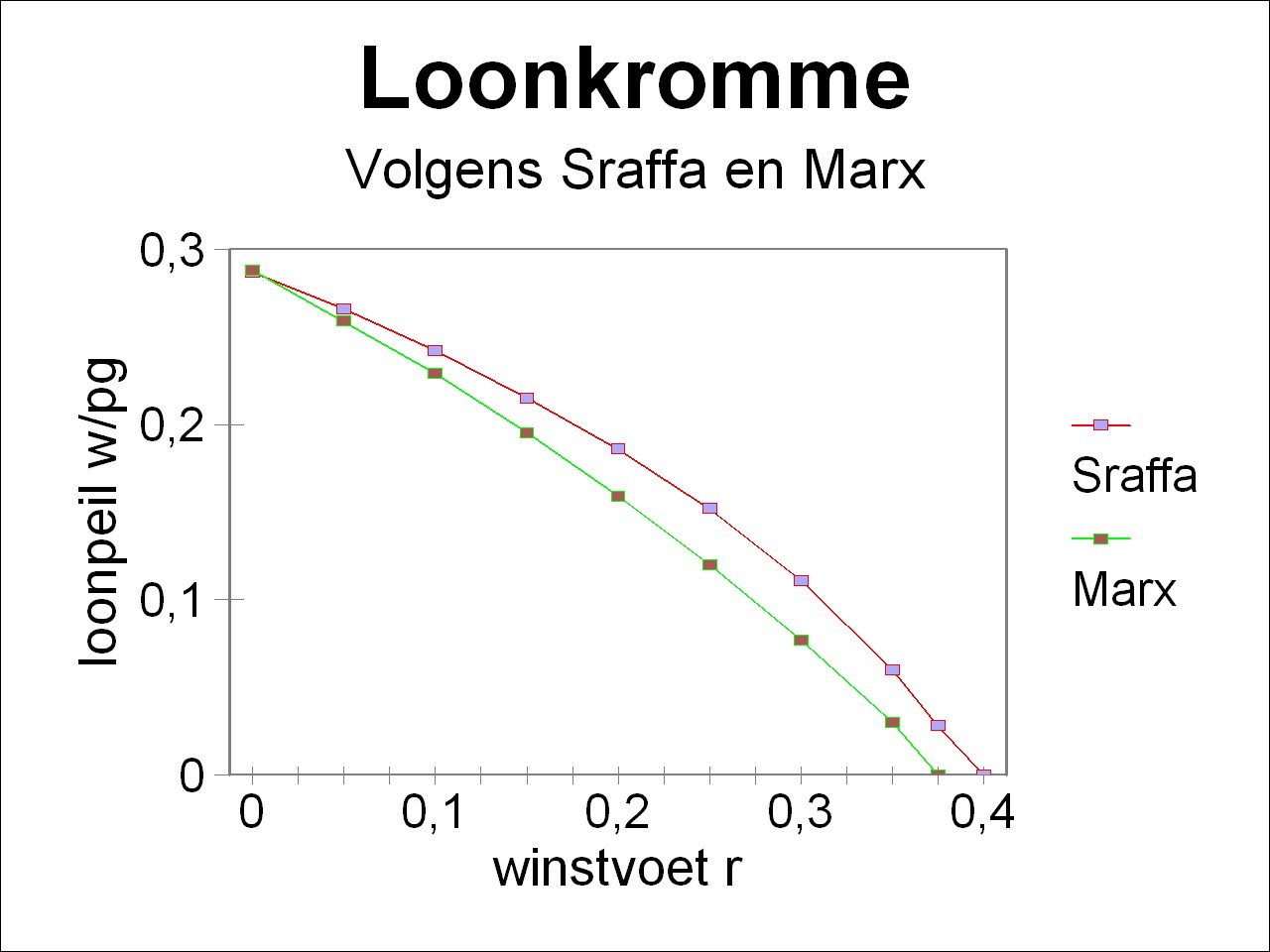
Figure 1: Wage curve w/pg according to Sraffa and Marx
This matrix equation can simply be solved, namely11
(9) η = a · (I − A)-1
In the formula 9 I is the unity matrix, and the upper index -1 indicates that the inverse matrix of I − A should be taken. From this solution it follows that a bale of corn is worth ηg = 3.479 labour units, and a ton of metal is worth ηm = 21.74 labour units. It is characteristic of labour values, that they do not depend on the distribution of the added value over the wages and the profits - this in contrast with the prices.
Now that the value of a unit product is known, all the production quantities can be calculated. For instance it turns out that cg=21.74 labour units, and cm=57.40 labour units. The social capital intensity is defined by
(10) κ = (cg + cm) / (lg + lm)
One finds with the help of the formula 10, that κ=2.638 labour units per labour unit. Now also the prices according to the theory of Marx can be calculated. The price transformation of the formula 4 is in matrix notation
(11) p = (η · A + w × a) × (1 + r*)
In the formula 11 w is the wage level of the factor labour, or in other words vi = w×li holds. If m is eliminated from the formulas 3 and 6, then one obtains for w the formula
(12) w = (1 − κ×r*) / (1 + r*)
Note that w is a transformation of the rate of surplus value m'. For from the formula 6 and the definition of the rate of surplus value it follows that w = v/l = 1/(1+m') holds. Therefore the formula 12 also shows how the general average profit rate originates from the rate of surplus value. The formulas 11 and 12 complete the price transformation of Marx. Thanks to the labour theory of value this price theory does not need the numéraire, in contrast with the theory of Sraffa.
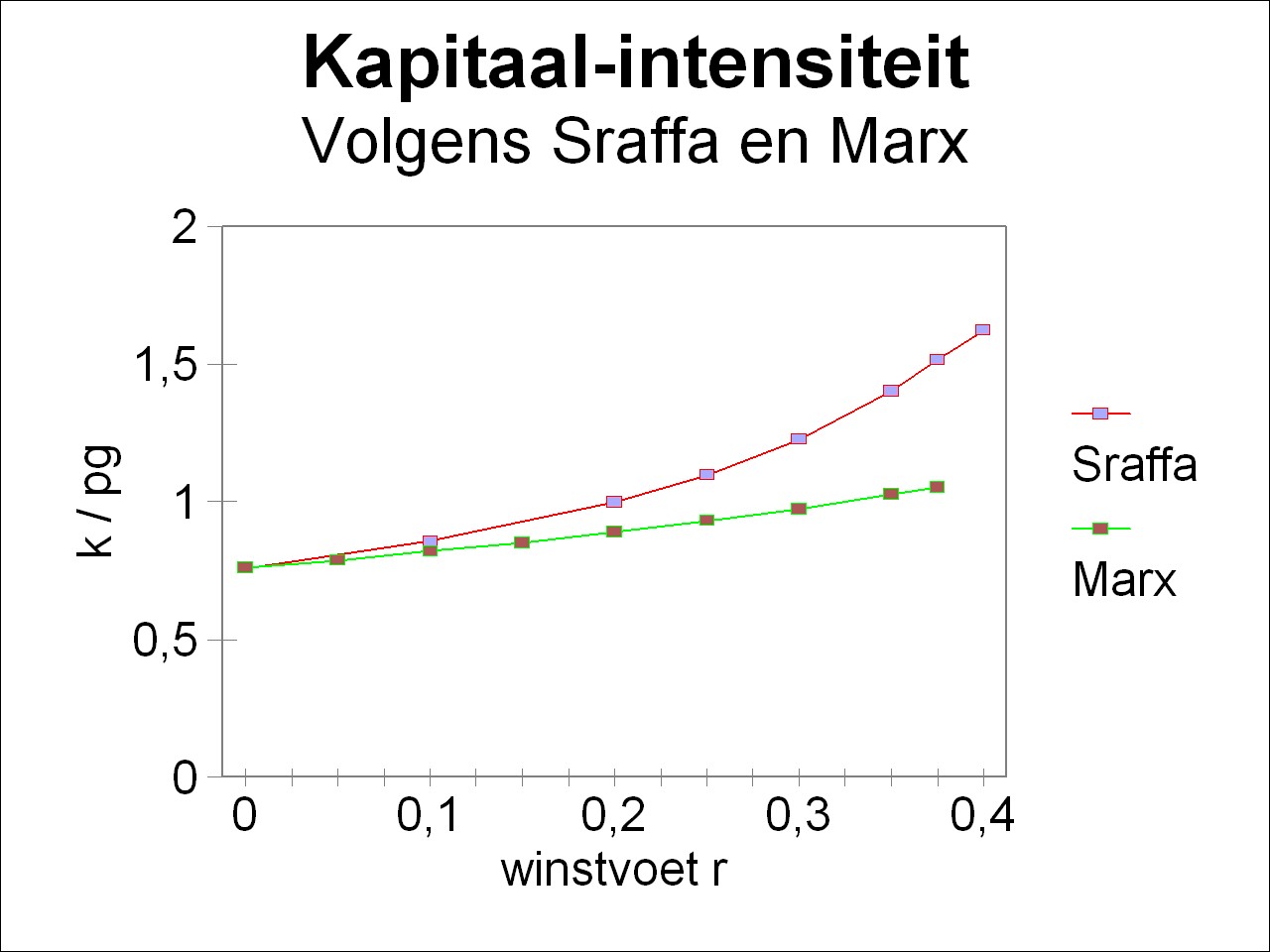
Figure 2: Capital intensity κ/pg as a function of the profit rare r
according to Sraffa and Marx
Now all is ready to illustrate the transformation problem in a comparison of the prices according to Marx and Sraffa. In this column the differences are shown by means of graphical presentations. The portraiture of the curves in the same figure requires that also the prices of Marx are normalized with the numéraire pg, just like in the example for the theory of Sraffa. In addition the wage level w must be converted. This is so, because in contrast with Marx the wage sum of Sraffa is not included in the advanced production capital12. In this way the quantities calculated with the theory of Marx are transformed, and they are added to the figures 2 and 3, which have already been incorporated in the previous column about the theory of Sraffa. Here the result is shown in the figures 1 and 2.
It is immediately striking, that in the case of a profit rate r equal to zero the results of Sraffa and Marx coincide. This is obvious, because then the workers receive the entire production, and thus the prices and labour values are the same. In this situation the surplus value is absent, so that a redistribution is not necessary. According as the profit rate increases, there is a growing discrepancy between the price transformation of Marx and the price system of Sraffa. This is particularly striking for the capital intensity κ/pg in the figure 2, where the difference becomes quite large. Incidentally here also the marxist κ-curve exhibits an upward trend, although in a moderate way (in contrast with the expectations of the neoclassical theory). In any case the two figures clearly illustrate the transformation problem13. In the example this problem occurs, because the organic compositions in the agriculture and in the industry are different. In the agriculture she is og=1.087/w, and in the industry om=5.71/w. Note that apparently the magnitudes of the organic compositions do depend on the distribution, but that their relative proportions are not influenced by her. Of course the profit rates in the branches r*g = mg/Cg en r*m = mm/Cm are also different, due to the formula 5. The figures 1 and 2 show that the theory of Marx does not succeed in compensating the profit rates in the two branches in such a way, that they transform into the profit rate according to Sraffa.
The tranformation problem can only be solved, if the theory of Marx is interpreted in another way. For this consult the book of A. Kliman, that is mentioned in a footnote.
Finally it must be remarked, that the wage curve and the curve of the capital intensity, that are calculated here with the theory of Marx, differ from those in the proof-text Vooruitgang der economische wetenschap. The marxist curves in the figures 8.7.1 and 8.7.2 of the proof-text are wrong.
- Your columnist knows this theory only through the three volumes of Das Kapital. It is asking too much to check the contents of this work by means of the other books of Marx (in posthumous publications), such as Theorien über den Mehrwert and Grundrisse der Kritik der politischen Ökonomie. But is must be acknowledged that the second and third volume of Das Kapital actually represent the interpretation, that Friedrich Engels applies to the ideas of Marx. Marx himself has always refused to publish his ultimate views. (back)
- See Reclaiming Marx's Capital (2007, Lexington Books) by A. Kliman. Although Kliman restores the logic in the theory of Marx, it must really be questioned that at the time Marx and Engels themselves were aware of this logic. Das Kapital is a work, that bases largely on the intuition of the authors. (back)
- Second hand bookshops offer a wide choice of pamphlets, for a few euros, that the Leninist parties and the Leninist states have distributed as propaganda material. Although the marxism in the Leninist states has been studied by scientists, they scrupulously have avoided the theme of the transformation problem! (back)
- In the modern economy the expenses are only called investments, if they are used for equipment. The expenses for raw materials and energy are not included in the investments, because they immediately flow back completely by the sale of the product. The income is as it were available at the moment, when the bill falls on the doormat. Therefore it is not really necessary to advance the "circulating" capital. Nevertheless Marx states that the expenses for this circulating capital also require a the realization of a profit rate r*. (back)
- See p.120 of his thesis Meerwaarde en winst (1976, SUN). (back)
- According to Marx the profit contains more than just the interest of the invested capital. For also the income of the producer, the rent for the leased land, and perhaps the taxes are included. This contradicts the neoclassical theory, where at least in the case of perfect competition the producer generally does not share in the profit. (back)
- See p.83 and further in Die Redundanz der Mehrwerttheorie (1989, Metropolis Verlag). Or p.33 and further in Grundzüge der neoricardianischen Preis- und Verteilungstheorie (2000, Metropolis Verlag). (back)
- Marx defines the department as a group of branches, that produces similar products. For instance a department can produce only consumptions goods, or only means of production, or only luxury goods. Sometimes the department of the means of production is again divided in two sub-departments. Then the first sub-department produces the means of production for the department of consumption goods, and the second sub-department produces the means of production for the first sub-department and for itself. Due to this method of Marx to divide the economy into separate groups he has been called a predecessor of Leontief and Sraffa. (back)
- The example originates from the chapter 6 of Vooruitgang der economische wetenschap (2011, E. de Bibelude), by E.A. Bakkum. Uitgeverij E. de Bibelude is a division of the Sociaal Consultatiekantoor. (back)
- The reader sees that this model assumes a simultaneity of the labour values. That is to say, the end products at the left hand side of the equation have the same labour value as the products, that enter the production process as input. There is no accounting for the possibility, that in the mean time the production technique may have been improved. If this would be the case, and the production process would have gained in efficiency, than the labour values of the end products would be less than those of the products that entered the production process. It is the merit of A. Kliman to have pointed to this phenomenon. His discovery has rendered harmless the criticism with regard to the supposed transformation problem. The argument to the contrary of Kliman does not only hold for the example, but obviously also for the preceding qualitative analyses of the transformation problem. (back)
- If the reader is unfamiliar with the matrix notation, then of course he or she can solve the set 7a-b by means of the substitution of variables. (back)
- The procedure is as follows. The price formula of Marx is p =(η·A + w×a) × (1+r*). Rewrite this as p = η·A×(1+r*) + w×a×(1+r*). Define wS = w×(1+r*). Then the price formula becomes p = η·A×(1+r*) + wS×a. Thus the wage level wS has been found, that results from the payment of wages at the end of the working period, just like Sraffa assumes. Then the wage sum itself does not yield a profit. (back)
- Perhaps a numerical comparison is useful. Suppose that the rate of surplus value m' is equal to one, then the marxist formula 11 immediately yields the profit rate r*=0.159. The workers receive half the value, that they have added during the production process. In other words, they obtain half the nett product. In this case the real wage per worker consists of 0.05 bales of corn and 0.015 tons of metal. That is to say, w/pg = 0.05 + 0.015×pm/pg. If this expression is combined with the formula 12 from the column about the theory of Sraffa, then one finds a profit rate r=0.193. Apparently the profit rate according to Marx (0.159) underestimates the profit rate according to Sraffa (0.193) with almost 20%. (back)

