The labour theory of value of Sam de Wolff

First insertion on Heterodoxe Gazet Sam de Wolff: 3 may 2012

One of the most important questions in the economic science is the manner in which the product prices are brought about. She determines what the value is, that consumers attach to a certain product. Following Adam Smith and especially David Ricardo, Karl Marx has developed a theory of value, that makes the value of a product entirely dependent on the amount of labour time, which is expended for its production. The (exchange) value of a product is proportional to the amount of invested labour time. A product is a carrier of value, because human labour is accumulated in it¹. Although Sam de Wolff has always called himself a marxist, and felt like a marxist, the labour theory of value has not become a squeezing strait-jacket for him. As is already clear from the columns about the conjuncture, De Wolff tries to renovate and advance the marxist theory. He has this urge to improve also with regard to the labour theory of value. In this sense De Wolff is a child of his time. For already in the final days of Karl Marx a new price theory had arisen, which makes the product exchange dependent on the considerations of utility, and not on the amount of needed labour time. The essence of this theory is, that the consumer wants to maximize the utility of his expenses. This idea was already advanced in 1854 by the economist Hermann H. Gossen, but it would take another twenty years before it is worked out into a usable model by the economists William S. Jevons and Léon Walras. The new theory is hostile towards marxism as far as the exploitation of the workers by the producers is denied.

The theory of utility was accepted quickly by the Dutch economists, even those who called themselves marxists. To the knowledge of your columnist only two Dutch marxists have really studied the conflict between the traditional labour theory of value and the theory of utility. This is of course Sam de Wolff, as will be explained further on in this column, and in addition the then quite well-known Rudolph Kuyper². De Wolff is not really interested in the price formation herself, but mainly in the total size X of the national production. In other words, he tries to determine the factors, which fix the gross national product. He hopes that this information can support and complete his model of the economic conjuncture. Although De Wolff embraces the theory of utility, he still wants to furnish his argument with his own designations for all sorts of economic quantities and phenomena. For instance, he is not very pleased with the word utility and prefers to use the word pleasure (in Dutch lust). This column adopts his designation, in order to preserve the originality of his thinking.

De Wolff states that the acquisition of products is accompanied by a pleasure L. On the other hand the provision of productive labour is accompanied by a displeasure O (in Dutch onlust). The property of a certain amount x of a product yields a pleasure L(x). If a consumer acquires an extra amount Δx of a product, then the accompanying extra pleasure ΔL(x) will decrease progressively. For the human ability to consume has its limits, albeit that this limit is stretchable. Of course the pleasure has a time horizon, so that the need is felt within a certain period. The delay of a consumption to later times is not taken into consideration. In other words, today a consumer may be satiated, but tomorrow the need will return. Tomorrow's need is excluded from the pleasure sensation. In the economic science the amount of utility, that is supplied by the last added unit of product, is called the marginal utility. Due to obscure reasons De Wolff dislikes the concept of the marginal utility³. Therefore he defines his own quantity, which he calls the intensity of pleasure LI. However, its definition coincides with the marginale utility, namely

(1)     LI(x, Δx) = ΔL(x) / Δx

In the formula 1 x is the amount of product in possession of the consumer, Δx is the additional amount dat he can get, and ΔL is the additional pleasure⁴. The remark just made about the progression ("become satiated") implies, that the intensity of pleasure diminishes according as x increases. At the end of this column an example will be presented, where the progressive decrease is clearly shown.

The displeasure (called by De Wolff the grief, or effort) of labour is represented by O(t), where t is the duration of the expended labour (in given units, for instance hours, months or years). It is generally assumed, that the displeasure increases in a progressive way, according as the labour time increases. For the workers prefer to enjoy some leisure time for relaxation and recreation. Of course the displeasure O(t) is defined within a given period of time. It makes a clear difference whether for instance five working days are imposed for the period of a week or for the period of a year. It is evident that a worker can never work longer than the time period, which relates to the displeasure. In passing it should be noted, that in the common economic theory the willingness to perform labour is mainly coupled to the wage level. In the following it will become clear, that in the model of De Wolff the wage enters only in an indirect manner. The intensity of displeasure is defined as
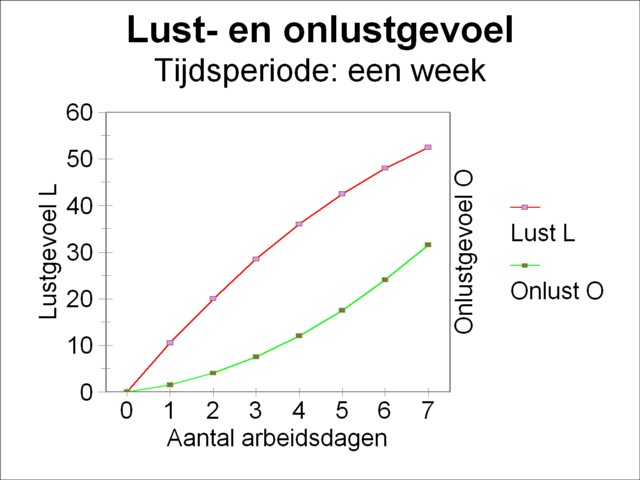
Figure 1: Example of pleasure and displeasure

(2)     OI(t, Δt) = ΔO(t) / Δt

In the formula 2 t is the duration of the expended labour, Δt is the additional time that the person could work, and ΔO is the additional displeasure of the worker. This shows how the labour time enters in the theory of De Wolff. The intensity of displeasure rises according as t increases (see also the example at the end of this column).

For convenience's sake De Wolff studies a society, consisting of just one person. This is called a Robinsonade, because this single person lives on an island, as it were, just like Robinson Crusoë. In this case the person is both the consumer and the worker (producer). Then this person will have to weigh his pleasure and his displeasure. According as he works longer, his displeasure O(t) increases. At the same time he acquires a larger amount of product in this way, which augments his pleasure L(x). In order to make a quantitative comparison between O and L, both functions must have the same argument. Therefore in the labour theory of value of De Wolff the pleasure L(x) is converted into the corresponding pleasure L_τ(t). This begins with the realization that one unit of product is equal to (the amount of product which is produced in a single unit of labour time) × (the time τ, that is needed to produce one unit of product). Note that τ is the inverse of the labour productivity ap. In other words, τ = 1/ap. Then for a certain quantity of product x one obtains

(3)     L(x) = L(t × ap) = L_τ(t)

The second equality defines L_τ. The intensity of pleasure LI_τ is given by

(4)     LI_τ(t, Δt) = ΔL_τ(t) / Δt

Starting from this point, the Robinson-person can calculate exactly the duration t of labour time, which balances his senses of pleasure and displeasure. He will stop his work as soon as his labour produces more displeasure than the extra consumption justifies. In the breaking point the intensities of pleasure and of displeasure must be just equal, that is to say

(5)     LI_τ(t, Δt) = OI(t, Δt)

The formula 5 determines the size X of the production in a society of a single person. For from the equality the total amount of labour time can be calculated. The total size X is obtained by a multiplication with the labour productivity ap. X is just the quantity, that De Wolff tries to derive. Unfortunately the limited practical applicability of the Robinsonade detracts somewhat from the success of the model. The income from capital or from rent is missing. In a society of a single person there is no wage struggle⁵.

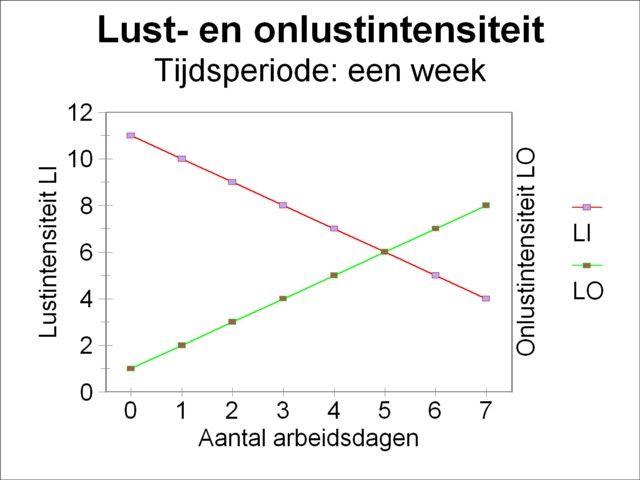
Figure 2: Example of intensities of pleasure and of displeasure

Concrete examples always help to clarify a model, and De Wolff himself persistently uses them. Suppose that the Robinson-person grows corn, in order to provide for his need of bread. The unit of corn production is a sack of corn, and the unit of labour time is a working-day. Assume that the labour productivity of the Robinson-person is given, for instance a quarter of a sack of corn per working-day. The formula 3 shows, that then the pleasure can be expressed in terms of the duration t of labour. Suppose that one has

(6)     L_τ(t) = (11 - ½ × t) × t

Further suppose that the displeasure is given by

(7)     O(t) = (1 + ½ × t) × t

It has already been observed, that both the functions L_τ and O are defined with respect to a certain period of time. In this example a time period of a week is chosen (that is to say, 7 units of labour time). Both functions are presented in the figure 1. The figure clearly shows, that neither the pleasure nor the displeasure is proportional to the labour time t. This effect has already been found at the beginning of the present column. The pleasure flattens, when the product quantity increases. On the other hand the displeasure of labour continues to grow, when t gets larger. The Robinson-person must calculate from the two functions L_τ and O the intensities, if he wants to calculate his optimal labour time t_opt by means of the formula 5. Besides he has to decide whether t consists of only working-days (in other words, it is a natural number), or whether t can contain a fraction of a working-day (in other words, t is a rational number)⁶. For convenience's sake it is assumed here, that the person is willing to work a fraction of a day, if need be. In that case Δt can become arbitrary small, so that the formulas 1 and 2 for the intensities can be interpreted as the derivates to t of respectively the pleasure L_τ and the displeasure O. The result is

(8)     LI_τ(t) = 11 - t

and

(9)     OI(t) = 1 + t

Both intensities are shown as graphs in the figure 2. The breaking point is found by substitution of the formulas 8 and 9 in the formula 5. One finds as the result, that the pleasure and displeasure are in balance, when the Robinson-person works during exactly t_opt=5 days. The same result is obtained by reading in the figure 2, where the point of intersection of the two curves is located. As long as the person works less than 5 days, he will long for extra sacks of corn. As soon as he keeps working after the fifth day, he will dislike the extra labour in relation to the added pleasure of corn. He will have left 2 days of his time period for relaxation. Because of the assumed labour productivity the total amount X of product for the given time period is equal to 1¼ sacks of corn.

1. The most well-known work of Karl Marx is Das Kapital, which consists of three volumes. In that book Marx defines right at the start the concept of value, namely in paragraph 1 of chapter 1 of the first volume. The paragraph is titled Die zwei Faktoren der Ware: Gebrauchswert und Wert (Wertsubstanz, Wertgröß). The concept of use-value is intimately connected to what later has been called the utility of a product. (back)
2. Rudolph Kuyper is a marxist theoretician, who finally is appointed as an extraordinary professor. He wrote already in 1902-1903 a lengthy essay, entitled Over waarde, in the magazine De Nieuwe Tijd. Later that article is included in the volume Marxistische beschouwingen (at the beginning of the twenties in the last century, by various publishers, among whome Uitgeversmaatschappij Ontwikkeling en NV De Arbeiderspers). Kuyper plainly rejects the labour theory of value, but his arguments remain vague. Moreover he shows little appreciation for the theories of De Wolff. Conversely, De Wolff is highly critical and fierce about the views of Kuyper, even though his anger is probably partly of a polemical nature. See among others his book Voor het land van belofte (1954, Uitgeversmaatschappij G.J.A. Ruys). (back)

Figure 3: Labour participation and wage
3. De Wolff explains his objection on p.301 of his book Het Economisch Getij. His argument is that the marginal utility would depend on the amount of product, which the consumer acquires. It is unclear where this interpretation of the marginal utility is coming from. In any case she is not common, for normally the marginal utility is calculated for the last acquired UNIT of product. In other words, suppose that an amount of product Δx is acquired, and this yields an extra utility Δu. Then the marginal utility is given by Δu/Δx. If the consumer acquires a smaller amount of product, then the extra utility will also be less, so that the marginal utility remains (almost) unchanged. So the objection of De Wolff is a bit odd. (back)
4. It is usually assumed that the utility of a product can not be measured as a quantity. The utility can only be arranged in the right order, in the sense that a certain quantity of the product A is more useful than a certain quantity of a product B. This arrangement of utility is called ordinal, and not cardinal. On p. 297 De Wolff states without a clear argument, that the pleasure (utility) does allow for a cardinal quantification. He writes on p.297: "The idea itself had ripened, and now only the courage is needed to believe it". De Wolff is never fearful. (back)
5. If a model accounts for both the wage, the interest and the rent, then the gross national product can grow, while the wage remains unchanged. Therefore the wage level is commonly considered to be a separate quantity, independent from the national income. In such models the willingness to work is determined primarily by the wage level. The figure 3 shows, that two wage levels can be discerned. Below the wage level w₁ the willingness to work increases with a decreasing hourly wage. Then the workers need to work for instance also on sunday in order to earn a living. Between the wage levels w₁ and w₂ the income covers the existential needs. Then the workers will only accept longer working-hours, if the hourly wage actually rises. This is the range of wages, that pertains implicitly in the model of De Wolff. Above the wage level w₂ a higher hourly wage does not provide an incitation for the workers to accept longer working-hours. On the contrary, they prefer to spend their growing income on leisure activities. The labour time belonging to the wage scale w₂ corresponds, as it were, with the optimal labour time t_opt in the Robinsonade.
   Some time ago, your columnist discovered on internet the paper Gossens Theorie der Zeitallokation im Lichte neuerer Theorien (2000) by Daniel Dohrn, from the university of Munich. Here Dohrn interprets the theory of Hermann Heinrich Gossen, and presents a formalism, which is almost equal to the model of De Wolff. Although your columnist has not read the original book of Gossen, the paper of Dohrn is an indication, that De Wolff is actually inspired by Gossen. (back)
6. De Wolff considers both the case of an indivisible working-day and a divisible working-day. In the first case the formulas 1 and 2 are difference equations. Then the formulas for the intensities become slightly different than the formulas 8 and 9, namely: LI_τ(t)=10½-t and OI(t)=½+t. Although here the formula 5 also allows to calculate t_opt=5 days, this is coincidental. For with an indivisible working-day is is likely, that the optimum can not be reached exactly. Then the Robinson-person should satisfy himself with slightly too little pleasure, or slightly too much displeasure. (back)